具有循环加群的环的结构

刘伦刚

(中国科学院 武汉物理与数学研究所《数学物理学报》编辑部，湖北 武汉 430071)

1 若干引理

对于剩余类环,我们都是很熟悉的[1-3]，但对于具有循环加群的某环，它的结构怎样?我们是不太清的.本文的目的就是想借助剩余类环来达到了解具有循环加群的环的结构.

首先引用两个数论的定理来证明一个数论问题(即一元一次同余方程解的定理)：一元一次同余方程:

ax+b≡B(modn)

(1)

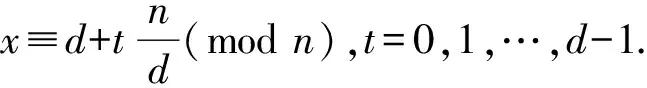
狄利克雷的算术级数的质数定理：假若(a,d)=1，那么形状象p=a+dt，t是正整数的质数有无穷多个.

引理1 若(k1,n)=d，则存在k, 使得k1≡kd(modn)且(k,n)=1.

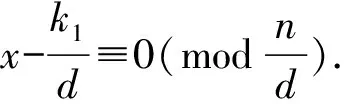
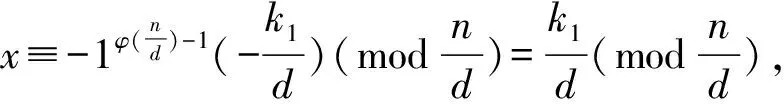
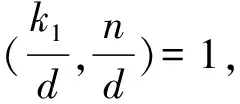
对于任何群G为循环群的充分必要条件是其子群恒为mG这样的子集，对于具有循环加群的环则有：

引理2 环R为具有循环加群的环的充分必要条件是其子环恒为mR这样的子集.

证明不妨设R={ka|k∈z} (以下R都具有这种形式)，∀m∈Z,mR={k(ma)|k∈Z}，关于加法，mR是R的循环子群．

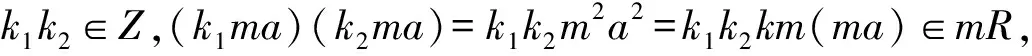
这样对于剩余类环Znk而言，由于它是具有循环加群的环，故∀k∈Z+，kZnk是环Znk的子环.

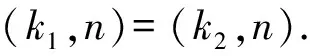
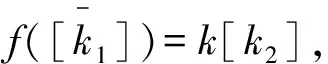
故 (k,n)=1.

(2)

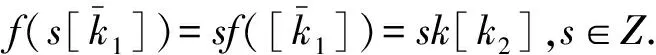
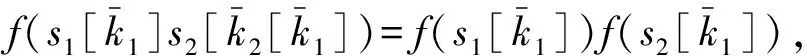
s1k1s2k[k2]=s1k[k2]s2k[k2]=s1s2kkk2[k2]，

也即：nk2|s1s2k2k(k1-kk2).取s1=s2=1,有n|k(k-kk2)，由 (n,k)=1,得n|k-kk2 ，故:

R1-kk2=αn，α∈Z.

(3)

由式(2)和式(3)，∀d∈Z,d|(k1,n)，则有d|kk2，由(n，k)=1，d|n， 有d|k2.又若d|(k2,n)得d|k1，故(k1,n)=(k2,n).

存在k， 使得：k1≡kd(modn)，且(k,n)=1.

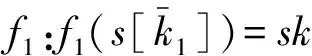
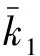
由n|k1-kd知，nd|s1s2kd(k1-kd)，s1s2∈Z，得:s1k1s2k[d]=s1k[d]s2k[d]，

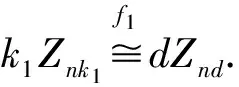
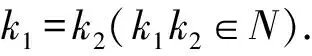
证明显然.

而由f(s1k1s2k1)=f(s1k1)f(s2k1)可得:s1kk1s2kk2=s1kk2s2kk2，得k1=kk2，这不可能，故k1=k2.

2 主要结果及其证明

定理1 环R关于加法成循环群，当|R|=n时，则它可嵌入到一个剩余类环中，当|R|=且a·a≠0时，则它可嵌入到一个整数环中.

证明由于R={ka|k=0,1,2,…}，那么存在某k使得a·a=ka.

这里当|k|=∞,a·a=0，不作讨论.

当|R|=n,a·a=0则取a·a=na，否则a·a=ka,1≤k≤n-1作映射φ:kZ→R(显然k≠0)

使得：φ(ks)=sa,s∈Z，则有φ(ks1+ks2)=(s1+s2)a=s1a+s2a，

故:

φ(ks1+ks2)=φ(ks1)+φ(ks2).

又φ(ks1ks2)=φ(ks1s2k)=ks1s2a=s1s2aa=s1as2a，故:φ(ks1ks2)=φ(ks1)φ(ks2)

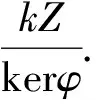
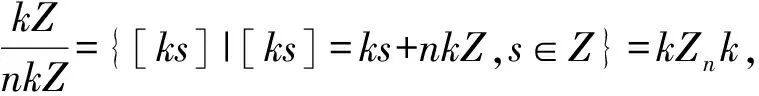
又当|R|=时，kerφ={ks|sa=0,s∈Z}={0}，故R≅kZ.

现在已经知道，若|R1|=|R2|=n，由定理1便可知：R1≅k1Znk1,R2≅k2Znk2(1≤k1,k2≤n).若|R1|=|R2|=且分别关于其加法生成元的乘法不为零元时有R1≅k1Z,R2≅k2Z.否则R1≅R2.

定理2 若|R1|=|R2|=n，则R1≅R2的充分必要条件是(k1,n)=(k2,n)；若|R1|=|R2|=，则R1≅R2的充分必要条件是k1=k2.

证明由引理3和引理4可知：k1Znk1≅k2Znk2⟺(k1,n)=(k2,n),k1Z≅k2Z⟺k1=k2.

由此问题便可以得证.

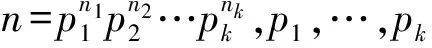
定理3 就同构的意义而言,n阶的环只有T(n)个，无限阶环则有无限个(这里指的环是具有循环加群的环，以下意义相同).

证明若|R|=n，则R≅kZnk,1≤k≤n.于是若d1≠d2，且都是n的正约数，则(n,d1)=d1≠d2=(n,d2)，于是d1Znd1≅d2Znd2.这就是说n阶的环至少有T(n)个.

又因(k,n)=d，则有kZnk≅dZnd，即R≌dZnd. 这即是说n阶的环不多于T(n)个.故n阶的环，就同构的意义而言只有T(n)个.

若|R|=时，则RZ≅kZ,k∈N，∀k1≠k2,k1,k2∈N，有k1Z≠k2Z.故无穷阶的环有无穷多个.

推论1 环R为域的充分必要条件是|R|=n,n为素数，且其加法生成元有a·a≠0.

证明⟹若a·a=0显然R不能为域，故a·a=ka，k≠0.这里当|R|=∞时，由定理1可知，R≅kZ但kZ是Z的子环不能为域，由此得出|R|=n，又有限域的特征必须是一个素数.故这里a的阶是n，故n必须为一个素数.

⟸若|R|=n，n为素数，且其加法生成元a有a·a≠0，而满足a·a=ka，则由定理1可知：R≅kZnk,0

推论2 设R是一个整环，若CharR=0，则R含有一个与Z同构的子环，若CharR=P，则R含有一个与Zp同构的子环.

证明定义φ∶Z→R为φ(n)=n·1.这里R1={n·1|n∈Z}，若CharR=0故R是整环，有|R1|=∞又1·1=1，由定理1得：R1≅Z，即R含有一个与Z同构的子环.

若CharR=P，因为R是整环，有：|R1|=P，由定理1有：R1≅ZP，即R含有一个与ZP同构的子环.

[1] 华罗庚.数论导引[M].北京:科学出版社,1979.

[2] 张禾瑞.近世代数基础[M].北京：人民教育出版社，1978.

[3] 谢邦杰.抽象代数学[M].上海：上海科学技术出版社，1987.