＊ 蕴含强(p,q)哈密尔顿性的几个条件

李瑞娟,张新鸿,李胜家

(1.山西大学数学与应用数学研究所,山西太原 030006;2.太原科技大学应用数学系,山西太原 030024)

＊蕴含强(p,q)哈密尔顿性的几个条件

李瑞娟1,张新鸿2,李胜家1

(1.山西大学数学与应用数学研究所,山西太原 030006;2.太原科技大学应用数学系,山西太原 030024)

利用路收缩技术,证明了,如果有向图D满足下列条件中的任何一个,

(1)最小半度δ0(D)≥(n+p+q)/2;

(2)D是(p+q+1)强连通有向图,且d+(x)+d+(y)+d-(u)+d-(v)≥2(n+p+q)-1,这里,x,y是任意控制顶点对,u,v是任意被控制顶点对;

(3)D的弧数超过(n-1)2+q2+p;那么D是强(p,q)哈密尔顿的.

路收缩;最小半度;度和;最少弧数;强(p,q)哈密尔顿

O157.5

A

本文仅考虑无环、无重边的有向图.设D是一个有向图,我们用n表示D的顶点的个数,用V(D)和A(D)分别表示D的顶点集和弧集.

设x,y是D上的两个顶点,如果xy是D的一条弧,那么我们称x控制y或者y被x控制,记作x→y.所有被x控制的顶点构成的集合称为x的外邻,记作N+D(x),所有控制x的顶点构成的集合称为x的内邻,记作N-D(x).记d+D(x)=|N+D(x)|,d-D(x)=|N-D(x)|,分别称为x的外度和内度.我们称x的外度或内度为它的半度.如果D是上下文所已知的,则我们忽略上述符号的下标.

有向图D的最小外度和最小内度分别是指δ+(D)=m in{d+D(x)|x∈V(D)},δ-(D)=m in{d-D(x)|x∈V(D)},最小半度是指δ0(D)=min{δ+(D),δ+(D)}.

对于D上的两个不同顶点x和y,如果存在顶点z,使得z→x且z→y,则称x,y是被控制顶点对.如果存在顶点w,使得x→w且y→w,则称x,y是控制顶点对.

本文中的路和圈是指有向路和有向圈.有向图D上的哈密尔顿路和圈是指包含所有顶点的路和圈.如果D包含一个哈密尔顿圈,则称D是哈密尔顿的.设P是D上的一条路,a,b是P上的两个顶点,不妨设在P上a在b之前,P[a,b]表示从a到b的子路.

如果对每一对顶点x和y,在D上总存在一条从x到y的路和一条从y到x的路,则称D是强连通的,或者称D是一个强连通有向图.如果在D上既存在从x到y的哈密尔顿路又存在从y到x的哈密尔顿路,则称D是强哈密尔顿连通的,或者说,D是强哈密尔顿连通有向图.如果|V(D)|≥k+1且对任何一个至多k-1个顶点的集合U,都有D-U是强连通的,则称D是k强连通的或者D是一个k强连通有向图.

定义1[1]设D=(V,A)是一个有向图,设S是以V(D)为顶点集的完全有向图中两两不相交的路的集合且S中所有路的总长度为q.如果对于所有满足上述条件的集合S,有向图D′=(V,A∪S)都有包含S的哈密尔顿圈,则称D是强q弧哈密尔顿的.如果对所有整数r(0≤r≤p)删除D的任意r个顶点得到的有向图是强q弧哈密尔顿,则称有向图D是强(p,q)哈密尔顿的.

显然,强(0,1)哈密尔顿有向图恰好是强哈密尔顿连通的.更多结果参看文献[6-8].

定义2[2]设x和y是有向图D上的两个不同顶点,P是以V(D)为顶点集的完全有向图上的一条(x,

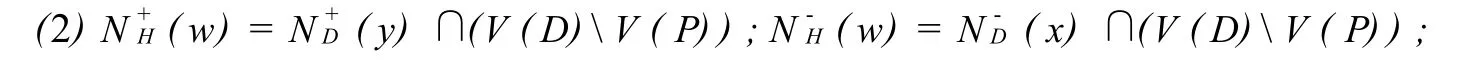
(3)一条两个端点均在V(D)V(P)上的弧属于H当且仅当它属于D.

记H=D/P.如果P是一条弧e,简单地记H=D/e.设

S={Pi|Pi是以V(D)为顶点集的完全图中的一条路,i=1,2,…,s,且这些Pi两两不相交}.如果H′=(…((D/P1)/P2)/…)Ps,则称H′是由D通过收缩S得到的有向图,记H′=D/S,不难看出,这里的收缩运算并不依赖于路收缩的顺序.

本文未给出的术语和符号可参考文献[1].下面是本文将用到的一些定理.

定理1[3]如果D是最小半度δ0(D)≥n/2,那么D是哈密尔顿的.

定理2[4]如果D是强连通有向图且对于D的任意控制顶点对x和y,以及D的任意被控制顶点u和v,有d+(x)+d+(y)+d-(u)+d-(v)≥2n-1,那么D是哈密尔顿的.

定理3[5]如果D的弧数超过(n-1)2,那么D是哈密尔顿的.

定理4 设p和q是两个非负整数且满足1≤p+q≤n-2.如果D的最小半度δ0(D)≥(n+p+q)/2,那么D是强(p,q)哈密尔顿的.

证明 设r是满足0≤r≤p的整数,D′是由D删除任意r个顶点的有向图.显然D′包含n-r个顶点.为了证明D是强(p,q)哈密尔顿的,只需证明D′是强q弧哈密尔顿的.设S是顶点集为V(D′)的完全图中互不相交的路的集合,且满足这些路的总长度为q.在有向图D′上通过收缩S构造新的有向图D″.由于在D′上每收缩一条弧,D′减少一个顶点,故D″包含D-r-q个顶点.进而y)路.称有向图H是由D通过收缩P到一个新顶点w得到的有向图,如果满足下列条件:

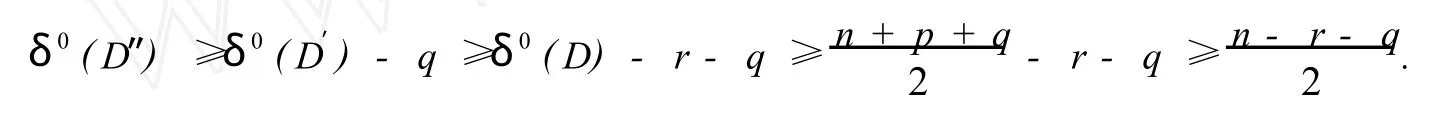
(1)V(H)=(V(D)V(P))∪{w};

根据定理1,D″是哈密尔顿的,从而D′是强q弧哈密尔顿的.结论得证.

引理设q≥1是整数且D是(q+1)强连通有向图,S是以V(D)为顶点集的完全图中两两不相交的路的集合且S中所有路的总长度为q.如果D′是由D通过收缩S得到的有向图,那D′是强连通的.

证明 设S包含的弧分别是e1,e2,…,eq,则(…((D/e1)/e2)/…)/eq=D/S=D′.显然,只需证明D/e1是q强连通的.令e1=ab,D收缩e1得到新顶点w.设x,y是D/e1中任意两个不同顶点.如果x和y都不是新顶点w,由M enger定理,在D上存在q+1条内部不相交的(x,y)路.如果这q+1条路中有q条路均不包含a,b,则D/e1有q条内部不相交的(x,y)的路.故假设这q+1条路中存在两条路P1和P2,使得a∈V(P1),b∈V(P2).注意到,P1[x,w]P2[w+,y]是D/e1上从x到y的路且与其余的q-1条路内部不相交,则在此情形下,D/e1上仍有q条内部不相交的路.因此,假设x或y是顶点w.不失一般性,假设x=w,由M enger定理,在D上有q+1条内部不相交的(b,y)路.显然,这些路中至多有一条包含顶点a.从而,其余q条(b,y)路仍是D/e1上的q条(w,y)路.再由M enger定理以及x,y选取的任意性,D/e1是q强连通有向图.结论得证.

定理5 设p和q是两个非负整数且满足1≤p+q≤n-2,D是(p+q+1)强连通有向图.如果对任意控制顶点对x,y以及被控制顶点对u,v.都有d+(x)+d+(y)+d-(u)+d-(v)≥2(n+p+q)-1,那么D是强(p,q)哈密尔顿的.

证明 设r,D′,S,D″如定理4所定义.显然D′是(q+1)强连通的,从而由引理,D″是强连通有向图.又显然,D″包含n-r-q个顶点.

类似于定理4的证明,只需证明D″是哈密尔顿的.设S′⊂V(D″)是收缩后得到的新顶点的集合.任取D″上的控制顶点对x,y以及被控制顶点对u,v.如果x(或y)是S′中的点,那么x(或y)在D″-S′上的外邻集与S中某条路的终点在D-S上的外邻集相同.仍用x(或y)表示这条路的终点.类似地,如果u(或v)是S′中的点,那么u(或v)在D″-S′上的内邻集与S中某条路的起点在D-S上的内邻集相同.同样地,仍用u(或v)表示这条路的起点.注意到,x和y(u和v)仍是D上的控制(被控制)顶点对,故有:

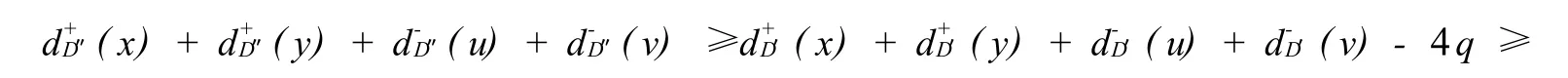
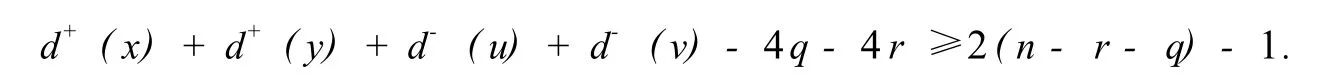
由定理2,D″是哈密尔顿的,结论得证.

定理6 设p和q是两个非负整数且满足1≤q2+p≤n-1.如果D的弧数超过(n-1)2+q2+p,那么D是强(p,q)哈密尔顿的.

证明 设r,D′,S,D″如定理4所定义.显然D′有n-r个顶点,D″有n-r-q个顶点,并且当删除D的r个顶点时,D至多减少了2r(n-r)+r(r-1)条弧.假设P是S中的一条路.如果在D′中收缩路P,那么D′至多减少了2|A(P)|(n-r-1)条弧.故当收缩S中所有的路时.D′至多减少了2q(n-r-1)条弧.因此

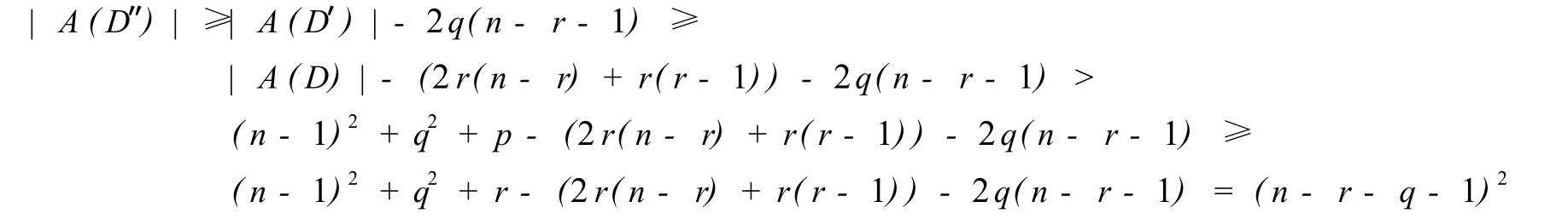
由定理3.D″是哈密尔顿的.从而,D是强(p,q)哈密尔顿的.

推论1 如果D的最小半度δ0(D)≥(n+1)/2,那么D是强哈密尔顿连通的.

推论2 设D是2强连通有向图.如果对任意控制顶点对x,y以及被控制顶点对u,v,都有d+(x)+d+(y)+d-(u)+d-(v)≥2n+1,那么D是强哈密尔顿连通的.

推论3 如果D的弧数超过(n-1)2+1,那么D是强哈密尔顿连通的.

[1] Bermond J C,Thomassen C.Cycles in Digraphs-A Survey[J].J Graph Theory,1981,5:1-43.

[2] Ban-jensen J,Gutin G.Digraphs:Theory,A lgorithm s and Applications[M].London:Sp ringer-verlag,2000.

[3] Ghouila-houri A.Une Condition Sufficante D’existence D’un Circuit Hamiltonian[J].C R Acad Sci Paris,1960,25:495-497.

[4] Zhao L C,Meng J H.A Sufficient Condition fo r Hamiltonian Cycles in Digraphs[J].Australas J Combin,1991,32:335-338.

[5] Lew in M.On Maximal Circuits in Directed Graphs[J].J Combin Theory Ser B,1975,18:175-179.

[6] Benvenuti D K,Punnen A P.SC-Hamiltonicity and Its Linkages with Strong Hamiltonicity of A Graph[J].SIAM J D iscrete Math,2010,23:2035-2041.

[7] Hsieh S Y,Kuo C N.Hamiltonian-connectivity and Strongly Hamiltonian-laceability of Folded Hypercubes[J].SIAM J Discrete Math,2007,53:1040-1044.

[8] Meierling D.Local Tournaments with the Minimum Number of Hamiltonian Cycles or Cycles of Length Three[J].D iscrete Math,2010,310:1940-1948.

Some Sufficient Conditions for Strongly(p,q)-Hamilton icity

LI Rui-juan1,ZHANG Xin-hong2,LI Sheng-jia1
(1.Institute of Mathematics and A pp lied Mathematics,Shanxi University,Taiyuan030006,China;
2.Department of Applied Mathematics,Taiyuan University of Science and Technology,Taiyuan030024,China)

U sing the path-contraction technique,w e p rove that if a digraphDsatisfies

(i)the minimum semi-degreeδ0(D)≥(n+p+q)/2(1≤p+q≤n-2),or

(ii)Dis(p+q+1)-strong andd+(x)+d+(y)+d-(u)+d-(v)≥2(n+p+q)-1 fo r every pairx,yof dominating vertices and every pairu,vof dominated vertices,or

(iii)Dcontains more than(n-1)2+q2+p;(1≤q2+p≤n-1)arcs,thenDis strongly(p,q)-Hamiltonian.

path-contraction;minim um semi-degree;degree sum;minimum arcs;strongly(p,q)-Hamiltonian

0253-2395(2011)01-0026-03＊

2010-05-24;

2010-06-28

山西省自然科学基金(2007011002);国家自然科学基金数学天元基金(11026162)

李瑞娟(1980-),女,山西侯马人,博士,讲师.E-mail:ruijuanli@sxu.edu.cn