＊ 一般重试时间、伯努利单重休假的离散Geom/G/1重试排队系统

朱翼隽,胡昌亮

(江苏大学 理学院,江苏 镇江 212013)

＊一般重试时间、伯努利单重休假的离散Geom/G/1重试排队系统

朱翼隽,胡昌亮

(江苏大学 理学院,江苏 镇江 212013)

考虑一个带有一般重试时间、伯努利单重休假的离散Geom/G/1重试排队系统.服务台前无等待位置,新到达的顾客若发现服务台忙或处于休假,则进入重试区域等待重试;若发现服务台空闲(不管有无顾客重试),就立即接受服务.顾客在完成服务之后,若重试区域中有顾客存在,则服务台以概率θ(0≤θ≤1)进行一次单重休假,以概率¯θ(=1-θ)重新等待顾客的到来;若重试区域中无顾客,则服务台也重新等待顾客的到来.利用马尔可夫链法,得到了本模型各个状态的稳态分布,并给出了系统顾客数的随机分解结果及关于其的一个应用.还给出了一个递推公式去计算重试区域顾客数的分布.最后用数值例子说明了一些参数对系统性能的影响.

离散重试排队;伯努利单重休假;随机分解;稳态分布

0 引言

由于离散排队在通信系统以及其他相关领域的应用,各种有关离散排队的研究得到了极大的重视.许多计算机和通信系统的信号传递问题都是发生在有固定间隔的时间段内,所以离散排队较之连续排队能更好的符合实际,并且近些年来出现了许多有关离散排队在应用方面的文章[1-3].

所谓重试排队,即顾客到达系统时,如果发现服务台忙,并且服务台没有等待位置,顾客就会进入重试区域等待再次重试.重试排队已经广泛的应用于电话交换系统、电信系统和计算机通讯系统等领域[4-6].在过去,重试排队的研究主要集中在连续时间上,但是自从 Yang和Li[7]首次将重试排队的有关问题推广到离散时间上,一些离散重试排队的研究陆续出现[8-11],但相比于比较成熟的连续重试排队的研究,这方面的研究还不够充分,需要进一步的完善.

在日常生活中,顾客在完成一次服务后,即使重试区域还有顾客存在,服务台也有可能进行休假.带有休假的连续重试排队的研究比较多[12-14],但有关具有休假的离散重试排队的文章很少.在实际生活中,服务员完成一次服务之后,可以根据重试区域顾客的多少,决定是继续为顾客服务还是选择进行一次单重休假,此即伯努利单重休假规则.本文在离散重试排队的基础上,加入一般重试时间及伯努利单重休假规则,得到了一些重要的稳态结果及数值分析结果.

1 模型描述

考虑一个离散Geom/G/1重试排队早到达系统,顾客的到达过程依据概率为p的Bernoulli过程.服务台前无等待位置,若顾客到达服务台时,发现服务台忙或者处于假期,就会进入重试区域等待再次重试;如果服务台处于空闲状态,则立即接受服务(不管此时重试区域队首顾客是否正在重试).服务台完成一次服务后,如果重试区域还有顾客存在,则服务台以概率θ(0≤θ≤1)进行一次单重休假,休假结束之后,重新等待为顾客服务,以概率¯θ重新等待顾客的到来;如果重试区域没有顾客,则服务台重新等待顾客的到来并为其服务.

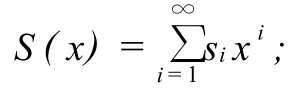
2 马氏链及稳态分布

在时刻m+处,系统状态可由过程Xm=(Cm,ξm,Nm)来描绘.此处Cm表示服务台的状态(0,1,2分别表示服务台处于空闲,服务,休假状态),Nm表示重试区域的顾客数,当Cm=0时,ξm表示剩余的重试时间;当Cm=1时,ξm表示剩余的服务时间;当Cm=2时,ξm表示剩余的休假时间.则其状态空间为:

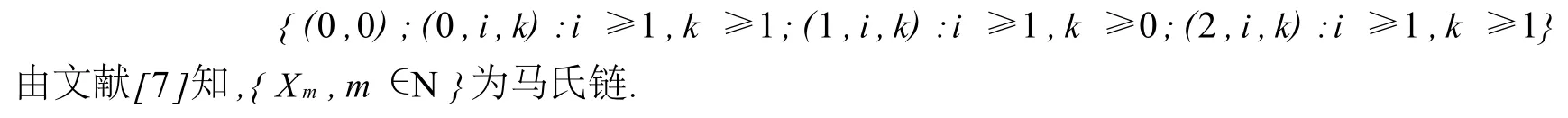
本文将研究马氏链{Xm,m∈N}的平稳分布,即

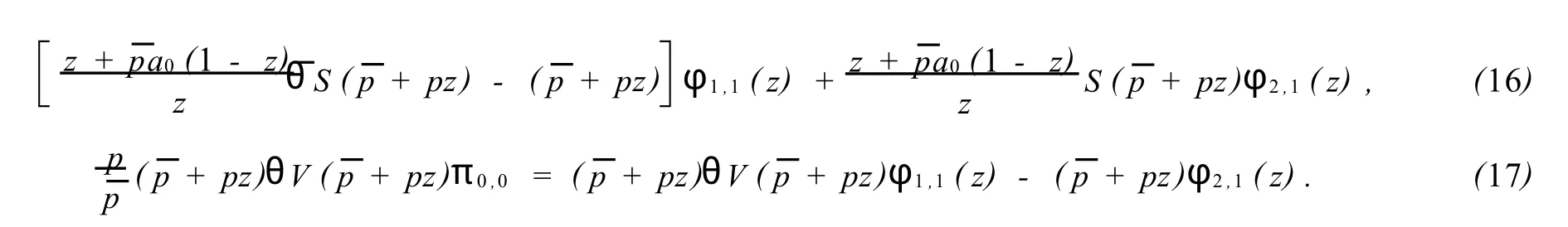
为了使研究能够继续,给出下面两个引理:

引理1 对于0≤x≤1,不等式A(x)≤x,S(x)≤x,V(x)≤x成立.

证明 由概率母函数A(x),S(x),V(x)的凸性可知,对于0≤x≤1,三不等式成立.

3 随机分解

随机分解原理是由Fuhrmann和Cooper[16]第一次引入排队系统的,起初随机分解原理在排队系统中的作用是分析各种休假策略对经典排队模型的影响,但随着研究的深入,它也可以用于比较复杂的离散重试排队系统中.

4 稳态概率计算

令ψk=P{N=k},则ψk表示重试区域顾客数为k个的概率.下面将会给出一个递推公式,用此计算本模型中重试区域顾客数分布的概率.

由定理4可以知道,若知道ψ(z)的各阶导数,重试区域顾客数的概率分布就可求得.

5 数值分析

在此部分,将会用数值例子来研究一些参数对系统性能的影响.假设p=0.1,并且重试时间,服务时间,休假时间分别服从参数为r,q1,q2的几何分布,则有分布

sj=q1(1-q1)j-1,vj=q2(1-q2)j-1,ai=ri(1-r),j≥1,i≥0,且0＜q1,q2＜1,0≤r＜1.

同时,约定q1=q2=0.5.下面讨论,对于不同的θ,系统非空的概率、重试区域平均顾客数分别与参数r的影响.

图1描绘了参数r与系统非空的概率之间的关系.由图1可以看出,对于不同参数θ,系统非空的概率是随着θ增大而增大的;图2描绘了参数r与重试区域平均顾客数之间的关系,可以看出,E(N)也是随着θ增大而增大的.同时可以知道,r值越大,对1-π0,0,E(N)的影响也就越大.

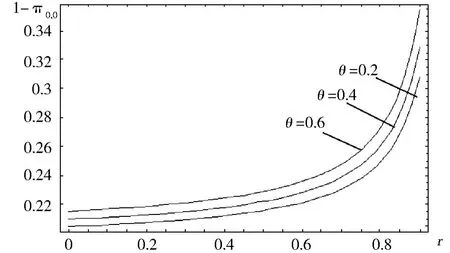
图1 系统非空的概率与 r的关系Fig.1 Relation between the parameter r and the probability of non-empty system

图2 重试区域平均顾客数与 r的关系Fig.2 Relation between the parameter r and the customers in obit site

最后,利用定理4给出的递推公式计算重试区域顾客数的概率分布.表1和表2(P49)分别阐明了在θ=0.3,0.6,r=0,0.3,0.6,0.9的情况下,重试区域顾客的概率分布情况.根据表中的结果,可以做出结论:随着θ的增大,重试区域中无顾客的概率是下降的,而重试区域中有非零顾客的概率是增大的;固定θ,可以看出,随着r的增大,重试区域中无顾客的概率也是下降的,而重试区域中有非零顾客的概率同样也是增大的.

表1 重试区域顾客数的概率分布(θ=0.3)Table 1 Probability distribution of queue length(θ=0.3)

表2 重试区域顾客数的概率分布(θ=0.6)Table 2 Probability distribution of queue length(θ=0.6)

6 小结

在这篇文章中,我们考虑了一个带有伯努利休假、一般重试时间的离散Geom/G/1重试排队系统,研究了它的稳态分布、随机分解及数值运算的结果,具有一定的现实意义.重试区域中的顾客除非接受服务后离开,否则就会一直等到接受服务.今后的研究可以将重点集中在带有不耐烦顾客之上,在此基础上,重试区域中的顾客就会根据具体的情况决定是继续等待重试,接受服务,还是选择离开.

[1] Bruneel H,Kim B G.Discrete-Time Models for Communication Systems Including A TM[M].Boston:Kluwe Academic Publishers,1933.

[2] Takagi H.Queueing Analysis:A foundation of Performance Evaluation,in:Discrete-time Systems[M].vol3,North Holland,Amsterdan,1993.

[3] Woodward M E.Communication and Computer Networks:Modelling with Discrete-time Queues[M].IEEE Computer Soc press,Los Alamitors,CA,1994.

[4] Artalejo J R.A Classified bibliography of Research on Retrial Queues:Progress in 1990-1999[J].Top,1999,7(2):187-211.

[5] Artalejo J R.A Classified Bibliography on Retrial Queues[J].Mathm atical and Computer Modelling,1999,30:1-6.

[6] Falin G I,Templeton J G G.Retrial Queues[M].Chapman&Hall,London,1997.

[7] Yang T,Li H.On the Steady-state Queue Size Distribution of the Discrete-time Geo/G/1 Queue with Repeated Customers[J].Queueing Systems,1995,21:199-215.

[8] Atencia I,Mo reno P.Discrete-time Geo[X]/G/1 Retrial Queue with Bernoulli Feedback[J].Com puters and Operations research,2004,31:359-381.

[9] Atencia I,Moreno P.A Discrete-time Geo/G/1 Retrial Queue with General Retrial Times[J].Queueing Systems,2004,48:5-21.

[10] 王金亭,赵青.两种失效模式下离散时间重试排队之研究[J].应用数学学报,2008,31(5):901-909.

[11] 陈佩树,朱翼隽,陈燕.有一般重试时间的 GeoX/G/1重试排队系统[J].江苏大学学报:自然科学版,2008,29(2):181-184.

[12] 陈佩树,朱翼隽,徐洁.有Bernoulli休假和可选服务的M/G/1重试反馈排队模型[J].数学的实践与认识,2008,38(11):92-102.

[13] 武惠玲,方春锋.有休假阀值M和顾客丢失的M/G/1重试休假排队系统[J].华南师范大学学报:自然科学版,2006(2):43-49.

[14] Aissani A.An MX/G/1 Energetic Retrial Queue with Vacations and it’s Control[J].Electronic Notes in Theoretical Com puter Science,2009,253(3):33-44.

[15] 孙微,田乃硕.带有准入规则的伯努利单重休假 Geomξ/G/1排队模型[J].燕山大学学报,2008,32(6):539-543.

[16] Fuhrmann SW,Cooper RB.Stochastic Decomposition in The M/G/1 Queue with Generalied Vocations[J].Ope-rational Research,1985,32:1119-1129.

[17] Artalejo J R,Falin G I.Stochastic Decomposition for Retrial Queues[J].Top,1994,2:329-342.

A Discrete-Time Geom/G/1 Retrial Queue with General Retrial Times and a Single Vacation Under Bernoulli Schedule

ZHU Yi-jun,HU Chang-liang
(Faculty of Science,Jiangsu University,Zhenjiang212013,China)

We consider a discrete-timeGeom/G/1 retrial queue with general retrial times,a single vacation under Bernoulli schedule.There is no waiting position in the server,and a new arriving customer finds the server busy or at vacation,he w ill join the orbit to retry getting the service,or he will accept service at once(No matter there is a retrial customer).After the service,the server either goes for a vacation with probality θ(0≤θ≤1)or may continue to wait the customer with probality¯θ,if there is a customer in the orbit at least;Ortherwise,the server may wait the customer too.Applying for Markov chain,w e derive the various steady state distributions of this system,and give a stochastic decomposition law of the system size and a application about it.A recursive form ular is also built up to facilitate the orbit site distribution.Finally,some numercial examples show the influence of the parameters on the system performance.

discrete-time retrial queues;a single vacation under Bernoulli schedule;stochastic decomposition;steady state distribution

O226

A

0253-2395(2011)01-0042-09＊

2010-03-20;

2010-07-16

国家自然科学基金(70571030;10571076)

朱翼隽(1945-),男,安徽歙县人,教授,博士生导师,主要从事排队论和随机网络方面的研究.