＊ 全向视觉中数据噪声对参数估计的影响

李晓明,王兰柱,田亚平

(山西大学数学科学学院,山西太原 030006)

＊全向视觉中数据噪声对参数估计的影响

李晓明,王兰柱,田亚平

(山西大学数学科学学院,山西太原 030006)

针对全向视觉中特有的数据特性,对图像中不同区域的数据噪声提出了不同假设,并在此假设下分析了数据噪声对线性参数估计的影响,研究表明,尽管远离图像中心区域的数据误差较大,但这些数据对参数估计的影响是非常大的.此外,还提出了一种分步选择数据点的方法,首先选择较高精度的数据得到初始参数估计值,然后逐步选择更多的数据点以保证得到尽可能多的数据点,而且所选择的数据点尽可能覆盖图像的边缘区域.实验结果表明,文章提出的方法可以得到更精确和更稳定的参数估计.

全向视觉;数据噪声;参数估计

0 引言

利用图像对应点估计模型参数是计算机视觉中的一类典型问题,如基本矩阵的估计、运动参数的估计、平面单应矩阵的估计等.文献中有大量与此相关的研究成果[1-4].标准的参数估计方法通常包括如下三个步骤[2]:(1)确定图像间的对应点;(2)采用线性算法进行初始估计;(3)采用某些统计优化标准通过非线性优化方法来进一步提高估计的精度.然而,第三步或最终的估计结果对前两步得到的初始估计是非常敏感的.本文主要研究全向视觉参数估计问题的第二步,即线性估计问题.

线性算法的不确定性,如上述提到的第二步,主要源自第一步的数据噪声.与传统透视相机相比,由于全向相机的非线性投影使得它的数据噪声更加严重.以鱼眼相机为例,图1给出了一幅典型的鱼眼图像.从图中可以看出,鱼眼图像中不同区域的变形差异很大,靠近图像中心的区域,其畸变与普通透视图像相似,离图像中心越远的区域,其畸变程度与透视图像相差越大.

图1 鱼眼图像靠近图像边缘的区域变形严重Fig.1 Much more distortion at the region near the border of a fisheye image

不同程度的变形导致数据的噪声情况不同.目前,针对全向视觉的特征检测和匹配方法很少,大多数情况下仍采用针对宽基线透视图像开发的基于仿射不变量的方法来实现特征检测和匹配[5-7].由于鱼眼图像局部并不满足仿射不变结构,因此可以想象,如果将这类基于仿射不变量的方法直接应用到全向图像中会带来一些相应的问题.比如说,在图像不同区域,其特征的检测精度可能不同,一般来说,离图像中心越远的区域,整体上误差比靠近图像中心区域的误差要大;再比如,图像中错误匹配点通常比透视图像中更多等等.本文我们将这些问题统称为数据噪声问题.如果这类问题不能很好地解决,必将对后续的参数估计问题产生灾难性的后果.就我们所知,目前还很少见这方面的相关研究.

为了抵抗数据噪声的影响,文献[8-9]建议利用大量的对应点并且用最小二乘法或统计技术来平滑噪声.在他们的研究中,作者假定图像中数据噪声为高斯模型,并没有考虑错误数据(outliers)和不同区域噪声不同的情况,然而错误数据可能导致不可预知的后果,噪声模型的偏差可能会影响最终模型估计的准确性.针对数据中存在错误匹配的情况,Micusik和Pajdla[10]提出了一种基于RANSAC[11]的全向相机极几何估计方法.并且他们的研究还发现,位于图像中心区域的对应点对模型具有较强的适应性,而那些远离中心区域的对应点对模型拟合起至关重要的作用.然而,在实际应用中的主要问题是由于越靠近图像边缘,对应点匹配越困难,而且特征点定位精度也越低.所以,针对全向视觉的数据特点,研究如何提高参数估计性能具有重要的意义.

本文以鱼眼图像运动参数估计为例,研究了数据噪声对参数估计的影响,并提出了一种可行的实施策略.第一,以前文献中假设不同区域的数据噪声模型是相同的,针对鱼眼图像变形的特点,我们对不同区域采用不同的噪声模型进行了实验分析,结果发现,如果仅选择较高精度的对应点,这些点通常不能很好的覆盖图像边缘区域,导致最终的模型估计精度降低;第二,为了包含更多远离图像中心的数据点,设定一个较大的误差容差阈值是必要的,但实验发现,设定一个单一阈值并不是最优的,我们给出的策略是采用分步迭代的方法,逐步选择越来越多的数据点.结果表明,使用这种策略,一方面可以得到更多的数据点,另一方面,数据集中包括了更多的远离图像中心的数据点.这两方面对噪声数据下的线性估计问题是非常有利的,并使得运动参数的最终估计在精确度和稳定性上得到了明显提高.

本文组织如下:第1节介绍一些线性估计和鲁棒估计技术的相关知识;第2节是建立在仿真实验基础上的数据噪声对参数估计的影响分析;第3节给出了一种实用的全向视觉线性参数估计技术;最后一节是全文结论.

1 相关知识

1.1 线性估计

以鱼眼图像本质矩阵为例,首先回顾一下标准的8点线性估计方法[12].假设两幅图像的对应点集合为(mi,′),i=1,2,…n,其中mi,′是对应像素点的测量坐标,如果摄像机已标定,根据成像模型和摄像机内参数可以计算出这些对应点所对应的空间向量 Xi和′,那么这些对应的空间向量之间满足极几何约束[13]:EX i=0,其中E是3×3的本质矩阵.如果给定至少8对图像对应点,那么可用SVD分解方法求出 E的初始线性估计.由于本质矩阵是一个自由度为5,秩为2的奇异矩阵,因此,得到 E的初始值后,标准的方法是,采用H artley提出的方法[12]进行强制约束,使得本质矩阵满足这些奇异约束条件.

我们知道,本质矩阵可分解为 E=T×R,其中,T和R分别为两摄像机的平移向量和旋转矩阵.采用Hartley的方法[12],可以从本质矩阵分解出旋转矩阵 R和相差一个比例因子的平移向量T.分解出运动参数T和R后,通常采用非线性优化算法(如Levenberg-Marquart)在五参数空间(三个旋转参数和两个平移参数)通过优化技术进一步提高估计精度.

1.2 RANSAC算法

RANSAC鲁棒估计算法[11]的基本思想是在进行参数估计时,不是不加区分地对待所有可用的输入数据,而是首先利用对应于具体问题所设计的搜索方法迭代地筛选出那些与所估计参数一致的“内点”(inliers),然后再利用所筛选出的所有inliers来估计参数.换句话说就是,随机选取一个最小数据点集获得一个模型,并计算这个模型的一致集,最大一致集对应的模型即为最优模型.

在RANSAC算法中,一个重要的参数是误差容差阈值t,该参数用来判断数据点是否与当前模型一致.尽管理论上该参数应该采用基于统计理论的方法确定,但由于统计的复杂性,一般根据经验确定.

2 数据噪声对参数估计的影响分析

这里的影响分析是基于仿真实验的.首先生成一定数量的空间三维点,然后根据投影模型分别投影到两幅图像,对这些图像点叠加不同的噪声,然后对采用线性估计方法计算得到的运动参数进行数据分析.实验内容包括3部分:(1)噪声模型的影响分析;(2)数据噪声的影响分析;(3)RANSAC策略的影响分析.

2.1 实验说明

(1)系统参数

相机的内参数是根据真实相机的配置设定的:

传感器:尼康D90(分辨率4288×2848)

镜头:Sigma 4.5mm f2.8 EX DC圆形鱼眼镜头 HSM,标称视角为180°,焦距为4.5mm,投影模型采用等角模型(equisolid angle projection).

外参数采用适中配置:T=[500,0,200]T,R=[0,0,π/6]T,需要说明的是,我们也曾对类似的平移参数和旋转参数进行了实验,结论基本是一致的,这里不再附上其他运动参数配置下的实验结果.

(2)数据生成

空间点是在一个半球空间按照均匀分布生成的.空间点P(x,y,z)的x和y方向取值范围都为[-∞,+∞],z方向,即深度方向从200到10 000(该参数接近一般的应用配置),空间点的数量为300.随机生成的空间点,通过已知的摄像机内外参数分别投影到两幅鱼眼图像,得到原始的理想对应点.然后再叠加不同的噪声,得到需要的实验数据.

实验中所用的外点(错误匹配点),直接在图像中随机生成.

(3)噪声模型

假设离图像中心越远的区域,对应点的平均测量误差越大,我们对不同区域采用不同的噪声模型来仿真这种情况.实验中,圆形的鱼眼图像按面积等分为三个区域(如图1)所示,噪声模型采用混合高斯模型,表示为:

其中μi分别表示区域i(i=1,2,3)中噪声的均值和方差.对于中心区域来说,μ1=0,采用标准高斯噪声.中间区域和最外区域的均值分别为μ2=1,μ3=2,方差都为σ=1的混合高斯模型.为了实验的简单化,我们假定仅第二幅图像数据受噪声干扰.

(4)误差度量

(5)关于RANSAC

RANSACV算法中的误差容差t采用角度误差,即球面向量与它对应的极平面的夹角误差,而不是常用的几何距离误差.通过简单的计算得知,对于我们采用的摄像机系统而言,图像坐标一个像素的距离误差近似相当于0.001 3弧度的角度误差.

2.2 噪声模型的影响分析

首先,我们对理想数据叠加两种不同噪声的情况进行了误差分析,一种是标准高斯噪声,即图像中所有区域都采用标准高斯噪声;另一种是不同区域叠加不同的混合高斯噪声.在这部分实验中,数据中没有添加错误匹配点(outliers),参与线性拟合的数据是所有误差小于3σ的点.表1(P63)是两类噪声数据采用线性算法得到的运动参数相对误差的均值和标准差,n是多次实验中对应点的平均数量.可以看出,两种噪声下的数据点基本相同,但标准高斯噪声下的估计误差小于混合高斯噪声的情况.这也说明,如果仅仅考虑数据噪声的情况,采用基于标准高斯噪声的假设,其最终结果偏于乐观.在接下来的实验中,我们假定图像点受混合高斯噪声干扰.

表1 不同噪声模型的误差比较Table 1 Error comparison for two different noise models

2.3 数据噪声的影响分析

假设整个数据集中没有错误匹配点,数据仅受噪声污染,噪声模型仍选用混合高斯模型.这部分我们主要分析选择不同精度的数据(或者说不同噪声的数据)对线性估计的影响.不同噪声数据的选择,我们采用RANSAC算法来实现.RANSAC算法中用不同的误差容差t得到不同的子集,通常,取较小的t意味着选取较高精度的对应点.由表2可知,随着t的增大,最终参数估计值的误差均值和标准差都逐步变小.这主要是因为,第一,当t增大时,参与最终模型拟合的内点数增加了,这对噪声数据的线性估计是非常有利的;第二,基于我们的假设,远离图像中心区域的对应点误差较大,当t增大后,参与模型拟合的数据覆盖了更大的图像范围,即可以选择更多远离图像中心的对应点参与模型拟合,正如文献[10]所述,远离图像中心的数据对全向模型拟合是非常重要的.我们也曾对不同t时的内点分布进行了统计,结果和预期是一致的,即t越大,内点中包含的远离图像中心的点越多.

需要注意的是,传统的透视图像中,通常先选择较大的t得到初始的参数估计,然后,在初始模型的约束下,通过减小t来逐步选择高精度点来提高参数估计的精度[14],然而,我们的实验发现,如果图像中不同区域的噪声情况不同的话,如本文所探讨的全向视觉的情况,那么这种误差容差t的选择策略是不妥的,这将会造成大多数内点集中在图像中心区域,严重影响最终的参数估计精度.

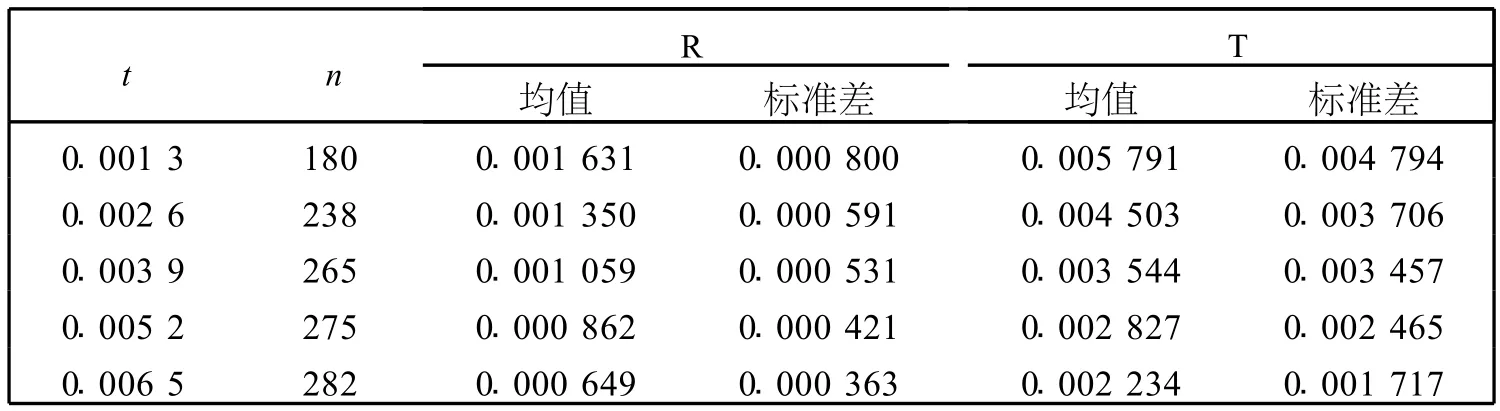
表2 不同噪声数据下的误差比较Table 2 Error comparison for data with different noise

2.4 不同RANSAC策略的误差分析

在实际应用中,不可避免地存在错误匹配点(外点).在这部分实验中,我们对实验数据不仅叠加了噪声,还在原来数据的基础上添加了不同比例的外点,噪声模型仍采用混合高斯模型,外点比例以10%的间隔从10%变化到50%,这种同时带有噪声和外点的数据更符合实际情况.我们知道,对数据中包含有外点的参数估计问题,通常需要采用鲁棒估计技术,这里我们选用基于RANSAC的鲁棒估计方法.

在RANSAC鲁棒估计方法中,误差容差t是一个重要的参数,通过这个参数来判断数据点是否为模型的内点,通常这个参数根据经验决定.一般说来,误差容差选得越大,得到的内点越多,但内点中也包含了更多大误差的数据点.表3(P64)列出了实验结果.为了得到更多的内点,选择误差容差t为0.006 5,s为外点比例,n为多次实验的平均内点数量.与表2中的第五行数据相比,在有外点的情况下,最终的估计精度要低于没有外点的情况,而且外点比例越大,精度降低得越多,这与我们的想象也是一致的.

尽管为了得到更多的内点,希望选择的误差容差t要大一些,但我们的实验发现,这种方法并不是最优的.这里我们提出一种新的RACSAC策略,这种策略得到的结果更加准确,稳定和可靠.首先,用较小的t得到较高精度的对应点,虽然内点数并不是足够多,但通过拟合这些内点得到的模型不会远离真实模型,即尽管得到的这个模型不够精确,但通常不会是一个随机结果.接着,用逐渐增大的t得到与当前模型一致的新内点集,并用新内点集来求解校正模型.重复这一过程,直到内点数达到稳定或t达到预先给定的阈值tmax.实验中,tmax设为0.006 5弧度,t以0.001 3弧度的间隔从0.001 3变化到0.006 5.通过比较表3和表4对应行的数据可以发现,其最终性能大大提高.第一,旋转矩阵误差的均值和标准差分别提高了37%和49%;平移幅度误差的均值和标准差分别提高68%和74%.第二,用这种方法得到的内点数基本等于对应点总数(注意,原始数据点共300个),但是传统的采用固定容差的RANSAC方法则达不到这个目标.第三,这种方法对外点数量也是鲁棒的.

表3 采用固定容差RANSAC策略的误差Table 3 Error with a fixed tolerance in RANSAC strategy

表4 采用可变容差RANSAC策略的误差Table 4 Error with a varied tolerance in RANSAC strategy

3 线性估计的一种实用方法

基于上一节的仿真实验误差分析,我们给出一种鱼眼图像运动参数线性估计的方法:

(1)确定图像对应点(文献中有大量经典的方法),记为集合S.

(2)从S中选择较高精度的数据集S0,用线性算法来估计初始基本矩阵 E0.这里数据集S0是用小的误差容差t0通过RANSAC算法得到的,这将得到一个可靠但不是非常准确的初始模型 E0.

(3)选择大于当前误差容差ti-1的新的误差容差ti,接着确定与当前模型 Ei-1一致的新内点集Si,最后用线性算法确定新的模型 Ei.

(4)重复(3)直到ti达到预先给定的阈值tmax或内点数量达到稳定.

(5)用文献[12]中的方法,分解最后的本质矩阵 E,得到初始的运动参数:旋转矩阵 R和平移向量T.

需要说明的是,在运动估计问题中,除了对应点的数量外,对应点的分布也是影响最终结果的一个重要因素,在本章我们的实验分析中,数据是采用均匀分布生成的,因此最终的结果误差都比较小.实际问题中,如果数据点在图像中分布不均匀时,文献[10]中给出了一种bucketing技术,通过在图像中的不同区域选择数据来拟合模型,是一种很有效的策略.另外,得到运动参数的初始线性估计之后,如果有必要的话,用非线性算法即标准算法中的第三步,能进一步提高运动参数的估计精度.

4 结论

由于鱼眼图像的非线性变形,使得它的数据噪声严重,定位误差比较大.对于数据受噪声干扰的运动参数的线性估计,为了抵抗噪声,需要建立大量充足的对应点,且点的分布尽量均匀,且运用恰当的鲁棒技术是必不可少的.本文我们对鱼眼图像运动估计中的数据噪声、鲁棒技术对运动估计的影响进行了实验和分析,并给出了一种运动参数估计的实用策略.使用这种策略,一方面可以得到更多的数据点,这对噪声数据下的线性估计问题是非常有利的,另一方面,数据集中包括了更多的远离图像中心的数据点.这两方面都使得运动参数的最终估计在精确度和稳定性上得到了明显提高,是一种实用的全向视觉参数估计方法.

[1] Zhang Z.Determining the Epipolar Geometry and Its Uncertainty:a Review[J].International Journal of Computer Vision,1998,27(2):161-198.

[2] Weng J Y,Huang T S.Motion and Structure from Two Perspective Views:Algorithms,Error Analysis and Error Estimation[J].IEEE Trans on Patter Analysis and Machine Intelligence,1989,11(5):451-476.

[3] Huang T S,Netravali A N.Motion and Structure from Feature Correspondences:A Review[C]//Proc.of the IEEE,1994,82(2):252-268.

[4] John Lim,Nick Barnes,LI Hong-dong.Estimating Relative Camera Motion from the Antipodal-Epipolar Constraint[J].IEEE Trans on Patter Analysis and Machine Intelligence,2010,32(10):1907-1914.

[5] Mikolajczyk K,Tuytelaars T,Schmid C,et al.A Comparison of Affine Region Detectors[J].International Journal of Computer Vision,2005,65(1/2):43-72.

[6] Mikolajczyk K,Schmid C.A Performance Evaluation of Local Descrip to rs[J].IEEE Trans on Pattern Analysis and M achine Intelligence,2005,27(10):1615-1630.

[7] Svoboda T,Pajdla T.Matching in Catadioptric Images with Appropriate Window s and Outliers Removal[C]//Proceedings of the 9th International Conference on Computer Analysis of Images and Patterns,2001:733-740.

[8] Spetsakis M E,Aloimonos Y.Optimal Visual Motion Estimation:a Note[J].IEEE Trans on Patter Analysis and M achine Intelligence,1992,14:959-964.

[9] Weng J,Ahuja N,Huang T S.Optimal Motion and Structure Estimation[J].IEEE Trans on Patter Analysis and M achine Intelligence,1993,15:864-884.

[10] Micusik B,Pajdla T.U sing RANSAC for Omnidirectional Camera Model Fitting[C]//Proc of the 8th Computer Vision Winter Workshop,Valtice Czech Republic,2003:153-158.

[11] Fischler M A,Bolles R C.Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].Communication of the ACM,1981,24(6):381-395.

[12] Hartley R.Multiple View Geometry in Computer Vision[M].2nd ed,Cambridge University Press,2003.

[13] Micusik B.Two View Geometry of Omnidirectional Cameras[D].Phd.Thesis,Czech Technical University,Prague,Czech Republic,2004.

[14] Matas J,Chum O,Urban M,et al.Robust Wide Baseline Stereo from Maximally Stable Extremal Regions[C]//Proc.of 13thBritish Machine Vision Conference,Cardiff,UK,pp.384-393,2002.

Im pact of Data Noise on Parameter Estimation in Omnidirectional Vision

L IXiao-ming,WANG Lan-zhu,TIAN Ya-ping
(School of Mathematical Science,Shanxi University,Taiyuan030006,China)

Based on the characteristics of data noise in context of omnidirectional vision,we assume different noise models for different regions in an omnidirectional image,and the effect of data noise on linear parameter estimation is studied.The results indicated that those data far from the image center have very important impact on the parameter estimation,though the data are less accurate.Furthermore,we also give a data selection method which is performed gradually.The initial model is estimated by using high precision data,and then mo re and mo re data are selected to ensure getting as more points as possible,meanwhile,the data selected should cover more regions near the image border.The experiment results show that this method can obtain more accurate and stable final estimate.

omnidirectional vision;data noise;parameter estimation

TP391

A

0253-2395(2011)01-0060-06＊

2010-09-20;

2010-10-28

国家自然科学基金(60773132);山西省自然科学基金(2009011020-1)

李晓明(1965-),男,山西灵石人,博士,副教授,主要研究方向为计算机视觉和图像配准.E-mail:lixm@sxu.edu.cn