算法多样化的实质与教学意义

●崔展 王文

算法多样化的实质与教学意义

●崔展 王文

1 引言

《全日制义务教育数学课程标准(实验稿)》明确提出：“提倡和鼓励算法多样化”[1]。近年来，算法多样化已成为广大教育者所关注的话题，诸多论者都认识到这一教学方式能够促进学生主动探索、积极思考。那么，它为什么会带来如此效果?

本文试图进一步探寻算法多样化的实质及教学意义，以此做到知其然并知其所以然，而对实际课堂教学有所裨益。

2 算法多样化的实质

2．1 算法及其由来

在数学活动中，有些方法经常被用到，以致于习惯化了，程式化了，譬如：

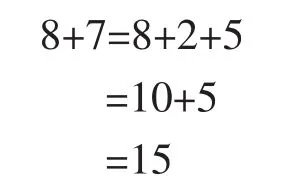
在这一计算过程中，第二个加数“7”被拆分成“2+5”以便于“8”和“2”凑成“十”。 这样一来，计算变得便利而合理。久之，这一方法(即“凑十法”)被固定下来，成为程式化的操作方法，这即是算法。

在上例中，先有主体参与其间的数学活动，然后在数学活动中产生算法。简言之，先有“数学活动”后有“算法”。人类发现数学知识的历史也正是如此。

2．2 算法传递及其弊端

在实际数学教学中，情形却并非如此。

当我们要讲授某一算法时，它早已为人们所发现。即算法是现成的，我们可以不必探索，而直接传递给学生。之所以这样做，原因有二：其一，现成算法预先存在，它使算法作为结果的直接传递成为可能；其二，较之让学生通过数学活动主动发现算法，直接传递的方式似乎更省时、更便捷。

但弊端也由此而产生，算法的直接传递，使得学生处于被动接受状态，久而久之，他们会形成不恰当的数学观念：学习数学就是接受课本上的一套算法，然后用这些算法解答习题。

2．3 “算法多样化”是对“算法传递”弊端的矫治

算法多样化，是指学生由于知识背景，思考角度不同而在同一题目中表现出多种解题方法的现象。譬如：在35-7的退位减法中，学生通过探索可以列出如下算法：

(1)35-1-l-1-l-1-l-l=28

(2)25+(10-7)=28

(3)(35-5)-2=28

(4)20+(15-7)=28

(5)(35-10)+3=28

(6)(35-15)+8=28

…

针对算法传递的弊端，中外数学教育家都强调，真正的数学学习不是一个“传递”的过程，而是一个重新发现的过程。唯有发现，才能达到真正的理解，“理解算法的最好途径就是发现它，没有什么比依靠自己的发现更令人信服”。

在数学活动中去发现算法，在发现中去掌握算法。算法不再作为唯一的、固定的模式来传递，这正是算法多样化的要义。要言之，算法多样化的实质就是数学发现。

3 算法多样化的教学意义

3．1 提供发现算法的机会

为明晰起见，我们以退位减法的学习为例进行分析：

35

-7

28

其步骤可表述为

35-7=20+(15-7) (个位不够减，向十位借“1”当“10”）

用教具进行演示，则可图示为：

国内辽河油田对采出液的热能回收利用方式为加热蒸汽发生器给水，由于换热温差的限制，仅通过换热器回收该部分热能并不能充分回收。因此，参考图1中余热回收流程，在国内气温较高不需要采用防冻系统的前提下，需要考虑采用其他技术手段利用这部分采出液余热。

如上，通常教学就是教师通过例题讲清算法的主要步骤与道理(如上例退位减的道理：个位不够减，向十位借“1”当“10”)，然后由学生仿照例题进行练习。

这种教法的实质就是试图直接传递算法：算法是唯一的、权威的、无庸置疑的；教师通过例题(配以教具演示)讲清算法与算理；学生接受算法，仿照例题做习题。

这里，不能说学生只有表面模仿。学生也达到了较深层次的理解：通过教具演示，学生懂得了算理(“为什么要借 1”，“为什么借 1 可以当 10”)。 问题在于，这里的算法被当作“绝对知识”进行传递。学生尽管理解了，但只是被动的理解与接受，整个教学过程没有为学生提供任何主动探索的机会。

如果采用算法多样化的教法，情形则刚好与此相反。

“我们现在要从35里减去7。这里有35根小棒，要从里面拿出7根，然后数数剩下有多少根。我们试试看，有几种拿法?”

实际课堂教学表明，学生可以找到如下几种算法(即拿法)

算法(拿法)一：

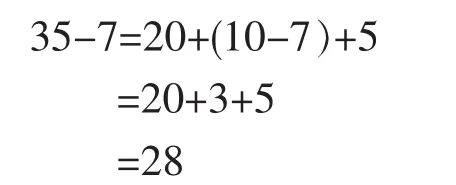
算法(拿法)二：

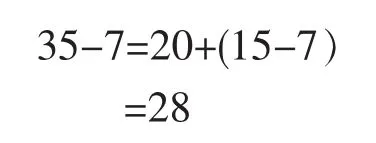
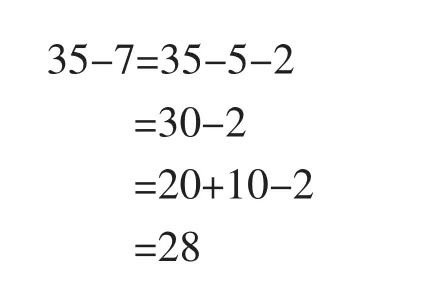
可以看出，让学生在对小棒的拆拆分分中亲历算法的产生过程，从而达到对知识的理解和掌握。正如皮亚杰所说[2]，知识是儿童在与外界的相互作用中，从内心自发生长起来的。算法多样化的教学恰恰提供了这样的机会，让不同经验背景和知识基础的学生，从不同角度思考同一问题，从而根据自己的理解找到不同的算法。

3．2 促进学生体会数学的必然性

数学是系统化了的常识，而且具有可靠性和必然性，如：3+2=2+3=5，常识要成为数学，必须经过提炼和组织，而凝聚成一定的法则(算法)。比如解答如下问题：一箱苹果24个，18箱苹果有多少个?

通常列出算式：24×18，即表示18个24相加求和；如果有情景支撑(比如小棒操作)，学生就会出现不同策略，如：

(1)20×18+4×18

(2)24×10+24×8

(3)24×20-24×2

策略的多样化表明了学生思维的丰富性和创造性。24可以分成20和4两部分；同样，18可以分成10和8两部分；思考的出发点和角度不同，亦即算法不同，而结果一致。“殊路同归”，这不恰恰有助于学生更深层次的理解数学知识的确定性和必然性吗?而我们固定的竖式乘法也正是对策略(1)的提炼和总结。

3．3 转变和完善“数学学习观”与“数学教学观”

算法单一化的学习往往使学生认为知识是 “绝对”的、“外在”的，数学学习不过是在老师条理清晰、层次分明的讲解或形象生动的演示下，理解算理，熟记算法；然后根据算法，模仿例题，再进行类似的练习以达到自动化。然而，有研究表明，长久采用这种教学方式，学生会只知算法。如果就算法背后的道理向学生提问，多数学生不能正确回答；而且越是简单的算法越容易被学生当作一套外在的规则来接受。换言之，算法单一化的教学，无法使学生主动探索和发现，不能从内心真正理解算理。

3．4 激发学习兴趣，培养创新精神

算法多样化使学生真正成为学习的主人，在以上两例中，如果算法过早的统一和“程序化”则会完全剥夺学生亲自参与知识建构的机会，从而禁锢学生原本丰富多彩的尝试和思考，这怎么可能引发学生的学习兴趣呢？教师们往往抱怨课堂时间紧，因此习惯把现成的算法直接呈现给学生。过早的使用形式化的语言讲解知识只能提供给学生一种复制的模版，学生没有了自己的思考，又怎么会有创新呢？算法多样化的教学过程恰恰促进了学生创新思维，因为对知识的理解和掌握必然伴有主体的重新建构。

[1]中华人民共和国教育部，全日制义务教育数学课程标准[s].北京：北京师范大学出版社， 2001．53，6.

[2]皮亚杰.发生认识论[M]．王宪钿等译，北京：商务印书馆，1996．16～2l.

崔 展/上海师范大学教育学院硕士研究生 王 文/山东省淄博市第十八中学

(责任编辑:刘 明)