R上自相似集的自相似测度的局部维数探讨

熊 波，邓 薇，孙 丽

(中南财经政法大学信息学院，湖北 武汉 430074)

R上自相似集的自相似测度的局部维数探讨

熊 波，邓 薇，孙 丽

(中南财经政法大学信息学院，湖北 武汉 430074)

研究了R上满足开集条件的一族压缩映射所生成的自相似集，讨论了其上给定的自相似测度μ的局部维数，在R中解决了Cawley和Mouldin问题。证明了在R中若{Ti(x)}ni=1满足开集条件，∀x∈G∩K， Cawley和Mouldin猜想成立，并且举出反例子验证当存在x∈G/K时，Cawley和Mouldin猜想不成立。

自相似集；自相似测度；局部维数；开集；压缩映射； Cawley和Mouldin猜想

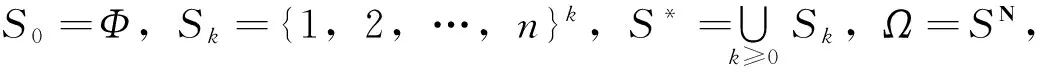
σ*i=(σ(1),…,σ(k),i)

若σ∈Ω，记σ|k=(σ(1),…,σ(k))，称为σ对k的限制。

对σ∈S*，称C(σ) 为由σ确定的Ω中的柱集：

C(σ)={τ∈Ω；τ|k=σ，|σ|=k}

J(σ|k)=Tσ(1)…Tσ(k)(J)

局部维数是分形几何理论中的一个重要的研究课题， Cawley和Mouldin在文献[6]中已证明。

命题1若K为Moran集，g(σ)=x，则：

1 主要结果

证明∀x∈G，以下分2种情形证明。

(Ⅰ)若x为某2个基本区间的交点，则有σ≠τ使得g(σ)=g(τ)=x。在这里，为了便于说明，定义序关系：若∃k，使σ(i)=τ(i)，1≤i≤k，且σ(k+1)lt;τ(k+1)，则称στ。不妨令στ，记：

B+(x,ε)=B(x,ε)∩[x,+∞)B-(x,ε)=B(x,ε)∩(-∞,x]

令：

则有：

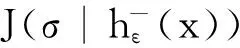
(1)

同理：

(2)

(3)

由式(1)和(3)得：

(Ⅱ)若x不是任何2个基本区间的交点，但x为某区间的端点，则存在唯一的σ∈Ω，使x=g(σ)。存在k0，使x为J(σ|k0)的端点。不妨设x为J(σ|k0)的右端点(左端点情况可作类似讨论)。则对∀τ，στ，J(σ|k0)∩J(τ|k0)=∅，记:

记:

则有：

与(Ⅰ)类似地可以证明：

证明设：

d=min{d(u,v),μ∈j(i),v∈J(j),i≠j,J(i)∩J(j)=∅}

D=max{d(T1(0),0),d(Tn(1),1)}gt;0

暂时固定εgt;d，t=minti，令：

hε(x)=max{k:B(x,ε)∩K⊂J(σ|k)}

则B(x,ε)∩K至少与J(σ|hε(x))的下一级2个基本区间相交，且：

μ(B(x,ε))≤μ(J(σ|hε(x)))

(4)

1)若B(x,ε)∩K包含J(σ|hε(x))下一级基本区间，则：

logε-logt≥log|J(σ|hε(x))|

(5)

根据式(4)和式(5)有：

2)若B(x,ε)∩K与J(σ|hε(x))的2个下一级基本区间相交，不妨令为J(σ|hε(x)+1)和J(τ|hε(x)+1),其中:

σ(i)=τ(i) 1≤i≤hε(x)σ(hε(x)+1)lt;τ(hε(x)+1)

如果J(σ|hε(x)+1)∩J(τ|hε(x)+1)=Φ，则∃y∈J(τ|hε(x)+1)∩B(x,ε)∩K，使得：

ε/2gt;d(x,y)≥t|J(σ|hε(x))|D

logε-log2dgt;logJ(σ|hε(x))

(6)

根据式(4)和式(6)可以类似地证明:

如果J(σ|hε(x)+1)∩J(τ|hε(x)+1)≠Φ，考虑J(σ|hε(x)+1)与J(τ|hε(x)+1)的下一级基本区间。

(a)若B(x,ε)∩K包含hε(x)+2级基本区间，则：

logε-2logt≥logJ(σ|hε(x))

(7)

根据式(4)和式(7)，可以得出结论。

(b)若B(x,ε)∩K不包含任一hε(x)+2级基本区间，则B(x,ε)必J((σ|hε(x)+1)*n)和J((τ|hε(x)+1)*1)相交，而这2个基本区间的间隔至少为t|J(σ|hε(x))|D，则∃y∈J((τ|hε(x)+1)*1)∩B(x,ε)∩K，使得：

ε/2gt;d(x,y)gt;t|J(σ|hε(x))|D

logε-log2tDgt;log|J(σ|hε(x))|

(8)

根据式(4)和式(8)可以类似地证明：

2 反 例

下面举出例子说明存在x∈K/G，使：

不成立。

令：

σ=10…010…010…010…，所以x∈KG。

g(σi)=g(τi)=yi

在本例中取后一种记法yi=g(τi)。于是J(σ|ki+1-1)∩J(τi|ki+1-1)≠∅，令εi=|J(σ|ki+1-2)|，有:

B(x,εi)⊃J(τi|ki+1-1)μ(B(x,ε))≥μ(J(τi|ki+1-1))

而：

故有:

从而结论不成立。

3 结 语

[1]Falconer K.Fractal Geometry-Mathematical Foundations and Applications[M].New York，John Wiley and Sons，1990.

[2]Moran P A R.Additive Functions of Intervals and Hausdorff Measure[J].Proc Camb Phil Soc，1946，(42)：15～23.

[3]Hutchinson J E.Fractals and Self-similarity[J].Indiana University Mathematics，1981,(30):714～747.

[4]肯尼思法尔科内著.分形几何中的技巧[M].曾文曲，王向阳，陆夷 译.沈阳:东北大学出版社，1996.

[5]Falconer K J.Wavelet Transforms and Order-two Densities of Fractals[J].J Statistical Physics,1992,67:781～793.

[6]Robert Cawley and R.Daniel Mouldin，Multifractal Decomposition of Moran Fractals[J].Advances in Mathematics，1992,92:196～236.

[7]陈二才，熊金成.关于自相似集的点态维数[J].科学通报，1998,43(20):2162～2166.

[编辑] 洪云飞

O174.1

A

1673-1409(2010)01-N017-04