一种基于模糊数学快速估价模型的改进

雷中英，谭肖笛

(长江大学城市建设学院，湖北 荆州 434023)

一种基于模糊数学快速估价模型的改进

雷中英，谭肖笛

(长江大学城市建设学院，湖北 荆州 434023)

工程估价是投资决策的一项重要内容。为了能达到快速精确的的预测目的，基于模糊数学的理论，采用指数平滑法，引入造价指数，对一己建立的模型进行了改进，使之在理论上更贴近实际造价。 实例证明，对该模型的改进是有效的。

模糊数学； 快速估价； 模型； 改进

基于模糊数学的工程造价估算方法是考虑到工程造价受到许多不确定性因素的影响，具有模糊性。文献[1]根据模糊数学原理，提出一种建筑工程快速估价模型，其通过确定特征向量、计算工程特征向量对比得到模糊隶属度及贴近度，从众多造价已知的典型工程中找出若干与拟建工程相似的工程，利用相似工程的造价作为原始资料，结合模糊数学的相关方法，对拟建工程进行造价估算[2]。该模型只考虑了拟建工程与典型工程的建筑结构与构造的相似性，并不能反映出因建造时间的差异所引起的价格费用的变化。为此，笔者采用指数平滑法，引入造价指数，对该模型进行改进。

1 快速估价模型

1.1建立典型工程的特征值矩阵

1)拟定若干个特征元素作为估价用的主要特征元素。用T表示工程特征集合,根据建筑工程对象的具体情况,选取m个能概括描述该工程的特征元素：

T={t1,t2，…,tm}

(1)

一般地说,上述模糊集合能够反映出某一建筑工程的主要特点。

2)从已建成的建筑工程中选取n个类似工程作为典型工程,设为A1,A2,…,An。

3)计算特征元素值。利用典型工程、拟建工程的特征元素基础数据和综合单价，计算建筑工程各特征元素值：

特征元素值=各分项工程占分部工程的百分比×综合单价×权重

(2)

4)设有n个典型工程组成对象集合，以m个特征元素作为建筑工程的主要特征元素，则n个典型工程m个特征元素组成特征值矩阵:

(3)

对典型工程Aj,对应特征向量：

对拟建工程B,对应特征向量：

1.2建立典型工程隶属度矩阵

隶属度是反映典型建筑工程特征值隶属于拟建建筑工程特征元素值的大小程度。隶属度计算采用如下公式：

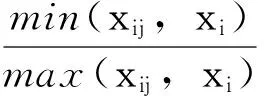
(4)

式中,rij为典型工程Aj的特征元素i对拟建工程的隶属度；xij为典型工程Aj特征元素i的特征值；xi为拟建工程特征元素i的特征值。

对典型工程特征值矩阵X通过式(4)转换,得到典型工程隶属度矩阵:

(5)

由式(5),可得到典型工程Aj对拟建工程的隶属度向量为：

1.3确定各典型工程与拟建工程的贴近度

各典型工程与预估工程的贴近度采用以下公式：

(6)

式中，uj为典型工程对拟建工程的贴近度；ri为拟建工程的特征元素i对自身的隶属度。

比较u1,u2,…,uj，取其中最大值max(uj)对应的典型工程计算拟建工程的造价。

PCR扩增仪DA7600型和高危型HPV核酸定量(16、18、31、33、45、52、56、58共8个型)检测试剂盒均由中山大学达安基因公司提供。Th1型细胞因子(IL-2、IFN-γ、TNF-ɑ)和Th2型细胞因子(IL-4、IL-6、IL-10)共6种均购自上海江莱生物科技有限公司。

1.4计算预估工程造价

(7)

2 对模型的改进

该模型只考虑了一个最为相似的工程，忽略了其余相似工程价格变化的影响，同时忽略了其他相似工程在时间价值上的影响，这在一定程度上会造成估算结果失真。笔者选取与拟建工程最相似的几个典型工程的造价作为原始资料,采用指数平滑法[4], 同时引入当年的造价指数，对其进行更正，从而得到拟建工程造价的预测值。设拟建工程的单方造价为E*,造价指数为L*，则：

(8)

3 案例分析

某地区综合教学楼工程建筑面积7418.9m2,6层, 钢筋混凝土框剪结构,桩基础，陶粒砖、混凝土墙，室外装饰主要为面砖，涂料墙面，室内装饰主要为乳胶漆。楼地面为地面砖、细石混凝土，要求用快速估价模型和改进后的模型分别对其进行估价(注：实际造价为 1751.8元/ m2)。

3.1拟定特征元素

T={层高，基础类型，门窗类型，内墙及装饰，外墙及装饰，楼地面装饰}，选取4个典型建筑工程A1,A2,A3,A4。典型工程和拟建工程的特征元素基础数据见表1。

表1 综合教学楼工程特征元素基础数据

3.2建立典型工程特征值矩阵

通过式(2)计算得特征值矩阵：

拟建工程特征向量 :

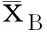
3.3建立典型工程隶属度矩阵

通过式(4)计算得出典型工程隶属度矩阵：

拟建工程对自身的隶属度向量为：

3.4确定典型工程与拟建工程的贴近度

u1=0.899u2=0.939u3=0.928u4=0.929u2gt;u4gt;u3gt;u1

选取贴进度最大的3个值，可知:

3.5计算拟建工程的造价

参考深圳市2009年11月20日发布的《深圳市建筑工程投标价格指数》，则有：

拟建工程的造价指数L*=1.32，其实际造价为E0=1751.8元/m2。

利用式(7)计算得：

利用式(8)计算得：

将两者进行误差分析，原模型的误差为:

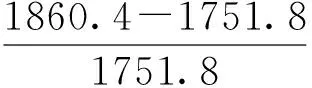
改进后模型的误差为:

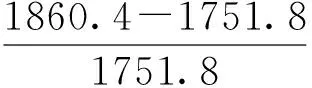
比较两者的结果可知，改进后模型的造价更贴近实际造价。

4 结 语

文献[1]中的模型只考虑了一个最为相似的工程，忽略了其余相似工程价格变化的影响，同时忽略了其他相似工程在时间价值上的影响，这在一定程度上会造成估算结果失真。笔者选取与拟建工程最相似的几个典型工程的造价作为原始资料,采用指数平滑法,同时引入当年的造价指数，对其进行更正，进一步缩小了价格的波动范围，使之与实际造价更接近。实例分析证明，对该模型的改进是有效和可行的。

[1]沈良峰. 建筑工程快速估价的一种模型及应用[J].工业工程与管理，2004，(6)：83～85.

[2] 马辉. 建设工程项目快速投资估算方法研究[D].天津：天津大学，2006.

[3] 张辉,朱大勇.模糊数学在工程快速估价中的应用[J].安徽水利科技，2004，(4)：17～18.

[4] 张传友.灰色系统理论在建筑工程快速估价中的应用[J].福建工程学院学报,2006，(2)：64～67.

[编辑] 李启栋

TU723.3

A

1673-1409(2010)01-N108-04