可变形储层注采过程中渗流场与应力场动态耦合分析

贾善坡，王 强

(长江大学城市建设学院，湖北 荆州 434023)

姚华彦

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

可变形储层注采过程中渗流场与应力场动态耦合分析

贾善坡，王 强

(长江大学城市建设学院，湖北 荆州 434023)

姚华彦

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

在油气开发过程中,油气的不断采出会造成地层压力的降低, 由此导致油藏的渗透率逐渐降低，从而使油井的产能降低。以多孔介质流-固耦合理论为基础，建立渗透系数、孔隙度等参数的动态演化方程，由此导出油气储层渗流-应力动态全耦合模型。对包含一个生产井和一个注入井的封闭区域进行耦合分析，在计算过程中对岩石孔隙度和渗透系数等参数进行更新，所获得的结论可为优化开采、后期开发调整、重复压裂、套管损坏预测等提供理论依据。

油气开采；渗流-应力耦合；孔隙压力；渗透性演化；有限元

地下流固耦合理论是渗流力学与固体力学交叉而生成的一个力学分支，是研究地质环境中流体(水、气、油)与岩体相互作用的一门科学[1,2]。随着石油工业的发展以及解决复杂石油工程问题的需要，石油工程中油藏渗流与应力耦合分析的研究也显得越来越重要, 储层上覆岩体重量由岩石骨架和孔隙流体共同承担，随着油气的不断开采, 必然造成储层孔隙压力的降低, 使得岩石骨架的有效应力增大，导致储层的压实。当油层压实时, 对油气生产将造成不利的影响，使得油藏的渗透率降低, 继而使油井的产能降低, 此外，油层的变形也影响油井和套管的变形与破坏。我国大多数油田均采用高压注水开采，在这种注采交变载荷作用下，油藏渗流与应力间存在很强的力学耦合作用，使得油藏应力场和渗流场的改变及其重新分布，导致油藏岩石物性参数的变化。因此，油藏渗流与应力耦合分析是石油工程中必须研究的重大课题，特别是为油气井定向钻井及井壁的稳定性分析、油气井水力压裂及岩石破裂机制研究、合理布置油气井网、预测油气开采动态和计算开采指标等提供理论基础和科学依据。笔者将岩石力学和渗流力学相结合，建立了流-固全耦合分析模型，该模型考虑了在油藏注采过程中的孔隙度和渗透性演化，真正实现了渗流场和应力场的完全耦合。

1 油藏流固耦合基本理论

(1)

增量形式的耦合方程为：

(2)

式中，[Ke]为单元刚度矩阵；[Kc]为固体单元与流体单元的耦合矩阵；[Ks]为单元渗流矩阵；{Δu}e为Δt时间段内的节点位移增量；{Δp}e为Δt时间段内的节点孔压增量；{ΔRF}e为Δt时间段内的节点载荷增量；{ΔRp}e为Δt时间段内的节点流量增量；θ为积分常数，取值范围为0.5～1。

2 油藏注采条件下孔隙度和渗透性的演化模型

图1 完全流固耦合系统相互作用的力学机理

完全流固耦合模型的相互作用机理如图1所示[3]，流-固之间的耦合是通过孔隙压力和有效应力显示相互作用的，而隐示的耦合作用是孔隙度的改变和渗透性的演变，孔隙度和渗透性的变化由有效应力的变化而引起，隐示耦合使得耦合系统呈非线性，导致多孔介质的孔隙度和渗透性呈各向异性。

对于油气储层多孔介质而言，在注采过程中，孔隙比的变化是由于岩石骨架的变形而引起的，可以表示为：

(3)

式中，Vp为孔隙体积;Vs为固相体积。假定岩石颗粒是不可压缩的，故岩石体积的变化为ΔV=ΔVp，根据体积应变的定义εv=εx+εy+εz可知：

(4)

式中，V0为初始体积;e0为初始孔隙度。

由式(4)可以导出孔隙度和体积应变之间的关系为：

(5)

式中，n0为初始孔隙度。

孔隙度与体积应变之间的相互关系如图2所示，从中可以看出，孔隙度越小，则变形对孔隙度的影响越明显。渗透系数与孔隙度之间的关系为：

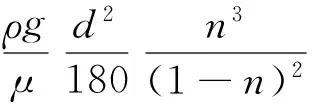
(6)

式中，μ为流体的动力粘度系数;d为固体颗粒的平均尺寸(直径)。

将式(5)代入式(6)可得到：

(7)

式中，k0为初始孔隙度。

渗透系数与体积应变之间的相互关系如图3所示，从中可以看出，孔隙度越小，则变形对渗透系数的影响越明显。

图2 孔隙度与体积应变之间的关系曲线 图3 渗透系数与体积应变之间的关系曲线

3 油气储层孔隙率与弹性力学参数之间的关系

多孔介质的体积模量和剪切模量取决于材料基质的属性、孔隙大小及分布和饱和状态等。目前用于材料组分及微结构估计多孔介质体积模量研究的主要理论方法有2种：①等效介质理论，包括著名的Voigt和Reuss的等效公式。②从多孔介质本构方程出发推导孔隙率和弹性力学参数之间的关系[5,6]。

设固体颗粒是不可压缩的，孔隙介质变形效应导致孔隙度和孔隙形状发生了改变，为了研究变形对孔隙弹性属性的影响，采用细观力学的方法进行描述。为了简化，不考虑加载过程中产生的各向异性。孔隙空间通过孔隙度n来描述，采用Hashin-Shtrikman上限方法来研究孔隙介质的弹性属性，孔隙介质的体积模量K和剪切模量G是孔隙度n的函数，可以表示为[7]：

(8)

式中，Ks和Gs分别为固相的体积模量和剪切模量。

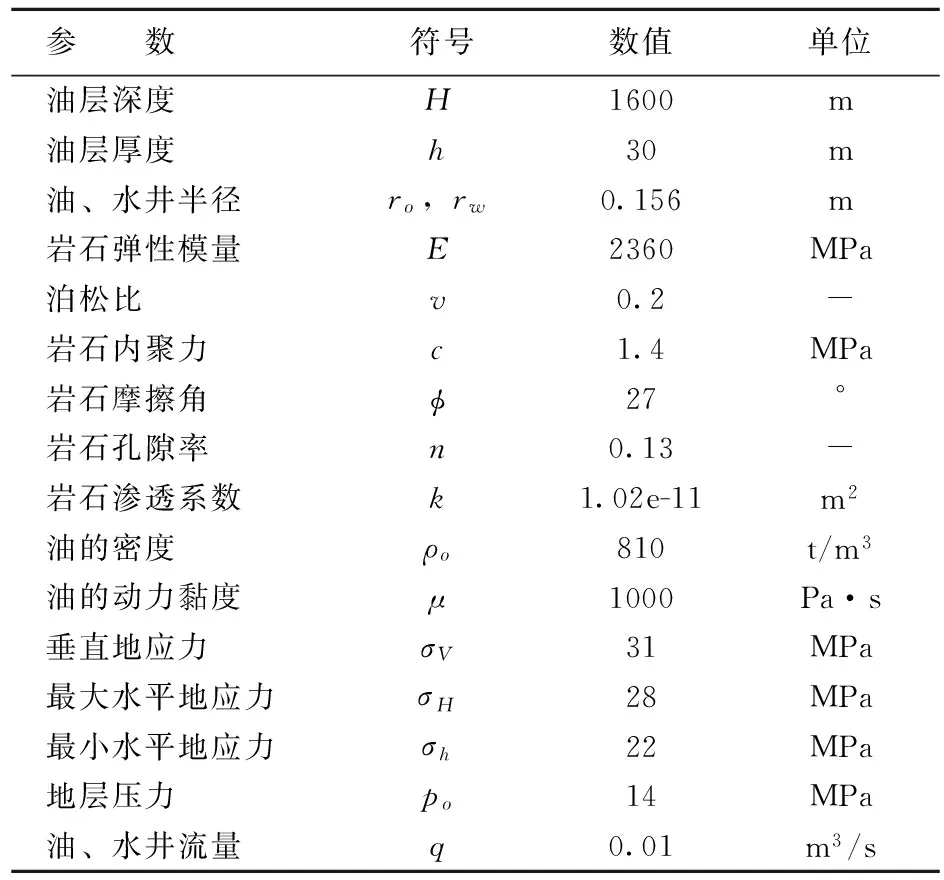
表1 某油田地层力学参数数据

在孔隙度为n0的条件下，可以通过实验室的试验确定K(n0)和G(n0)，代入式(8)即可求出Ks和Gs。另外，式(8)在石油工程、地球物理等方面有着广泛的应用前景，其对岩石的化学腐蚀及破坏扩容后性质的改变、渗流-应力的耦合等问题的研究有一定的指导作用。

4 算 例

下面用一个算例对文中提出的方法进行验证。该算例模拟的区域包括一个注水井和一个生产井，计算模型如图4所示，左下角为生产井，右上角为注水井，边界假定为不透水边界，模型x方向承受最小水平应力σh作用，模型y方向承受最大水平应力σH作用，计算模拟时间为500d，油藏参数如表1所示。

图4 计算网格图 图5 从生产井到注入井的孔压分布曲线

图5为储层注采过程中地层压力的变化趋势，从图中可以看出，注入井部位的孔隙压力是升高的，生产井部位的孔隙压力是降低的。

在注采过程中，渗透系数在耦合分析过程中是变化的，而且计算区域中各部位的变化幅度并不相同，变化的幅度与应力场有关，由于地应力的非均匀性，导致井眼附近的渗透系数分布呈各向异性，如图6所示。在注水井处，渗透系数增大，而在生产井处，渗透系数明显减小，但是随着时间的迁移，生产井部位的渗透系数略有升高。

图6 注采过程中地层渗透系数变化趋势

5 结 语

依据多孔介质流固耦合理论, 建立了渗流-应力全耦合分析的迭代计算模型，模型中考虑了储层孔隙度和渗透性的动态演化，导出了孔隙度、渗透系数等物性参数的动态模型，为流固耦合完全分析提供了有效的途径，并将该模型用于油水井注采过程的流固耦合模拟。实例计算结果表明，由于储层注采使得地层的孔隙压力和岩石骨架的有效应力发生了变化,使得油藏的孔隙度和渗透性等物性参数发生明显变化，并在油水井部位呈各向异性。文中的研究结论可为油田开发采取适当措施，达到最优开采目的提供可靠的依据，同时也为后期开发调整、重复压裂、套管损坏预测等提供理论依据。

[1]白矛,刘天泉.孔隙裂隙弹性理论及应用导论[M]. 北京：石油工业出版社，1999.

[2] 陈卫忠,吴国军,贾善坡.ABAQUS在隧道及地下工程中的应用[M]. 北京：中国水利水电出版社，2010.

[3] 贾善坡.Boom Clay泥岩渗流应力损伤耦合流变模型、参数反演与工程应用[D].武汉：中国科学院武汉岩土力学研究所，2009.

[4] 路保平,徐曾和.井眼周围可变性储层流-固耦合数学模型[J].石油学报,2006,27 (5):131～134.

[5]李春光，王水林,郑宏，等.多孔介质孔隙率与体积模量的关系[J].岩土力学,2007,28(2):293～296.

[6] 葛洪魁,韩德华,陈颙.砂岩孔隙弹性特性的试验研究[J]. 岩石力学与工程学报,2001,20(3):332～337.

[7]Bernaud D, Dormieux L,Maghous S.A constitutive and numerical model for mechanical compaction in sedimentary basins[J].Computers and Geotechnics,2006,33:316～329.

[编辑] 李启栋

TU443;TE31

A

1673-1409(2010)01-N104-04