纵、横波分离的数值模拟研究

何 艳

(西华师范大学数学与信息学院，四川 南充 637002)

纵、横波分离的数值模拟研究

何 艳

(西华师范大学数学与信息学院，四川 南充 637002)

从弹性波方程散度和旋度求取入手，通过引入等价方程，论证了纵波为无旋场、横波为无散场理论。利用有限差分模拟各向同性介质中的地震波场，并分别计算散度场和旋度场。结果表明，在满足差分范围内速度无剧烈变化的情况下，通过该方法能有效地分离出纵、横波场。另外，旋度运算的矢量性质造就了分离后的记录在震源两侧极性反向的特性，而这一特性与野外采集的横波数据在物理特性方面极其相似。

弹性波方程；纵波；横波；散度；旋度

通过弹性波方程数值模拟得到的是P波(纵波)和S波(横波)的混合波场。对于由P波震源激发记录中包含反射P波和转换S波的地震数据，可以通过散度和旋度的计算将P波和S波分离❶。弹性波纵横波场分离最初由Dankbaar[1]提出，Devaney等[2]利用极化波分解对弹性波VSP数据中的PS波场进行了分离；Dellinger等[3]在空间-频率域中利用散度和旋度因子对各向异性介质中的P、S波场进行了分离。笔者从弹性波方程散度和旋度求取入手，通过引入等价方程，论证了纵波为无旋场、横波为无散场理论，并利用有限差分模拟各向同性介质中的地震波场。

1 弹性波方程的散度与旋度

关于位移场U(u,v,w)的X方向二阶弹性波方程可以写为：

(1)

式中，u、v、w分别为x、y、z方向的位移；λ、μ为拉梅系数；ρ为密度。类似地，可以得出Y、Z方向的方程。

根据纵波速度Vp、横波速度Vs与拉梅系数λ、μ的关系：

从式(1)中消去λ、μ得:

(2)

引入纵波变量Up和横波变量Us：

Up={up,vp,wp}Us={us,vs,ws}

(3)

关于U(u,v,w)的弹性波方程可以写成关于Up(up,vp,wp)和Us(us,vs,ws)的等价方程组:

u=up+usv=vp+vsw=wp+ws

首先计算横波散度：

可见，横波散度为零，即横波为无散场。

再计算纵波旋度：

可见，纵波的旋度为零，即纵波为无旋场。

2 数值模拟

上述结论存在的前提是均匀介质，如果介质非均匀，纵波旋度和横波散度都将非零，因此，从单纯的数学意义上来说，非均匀介质中的弹性波场是不能进行波场分离的。但从另一方面考虑，如果应用有限差分来求导，数据应用范围只是差分范围内的数据点(数据点数与差分阶数有关)，在满足差分范围内速度无剧烈变化的情况下同样可应用上述理论来分离波场。下面仅以二维弹性波方程为例进行数值模拟。

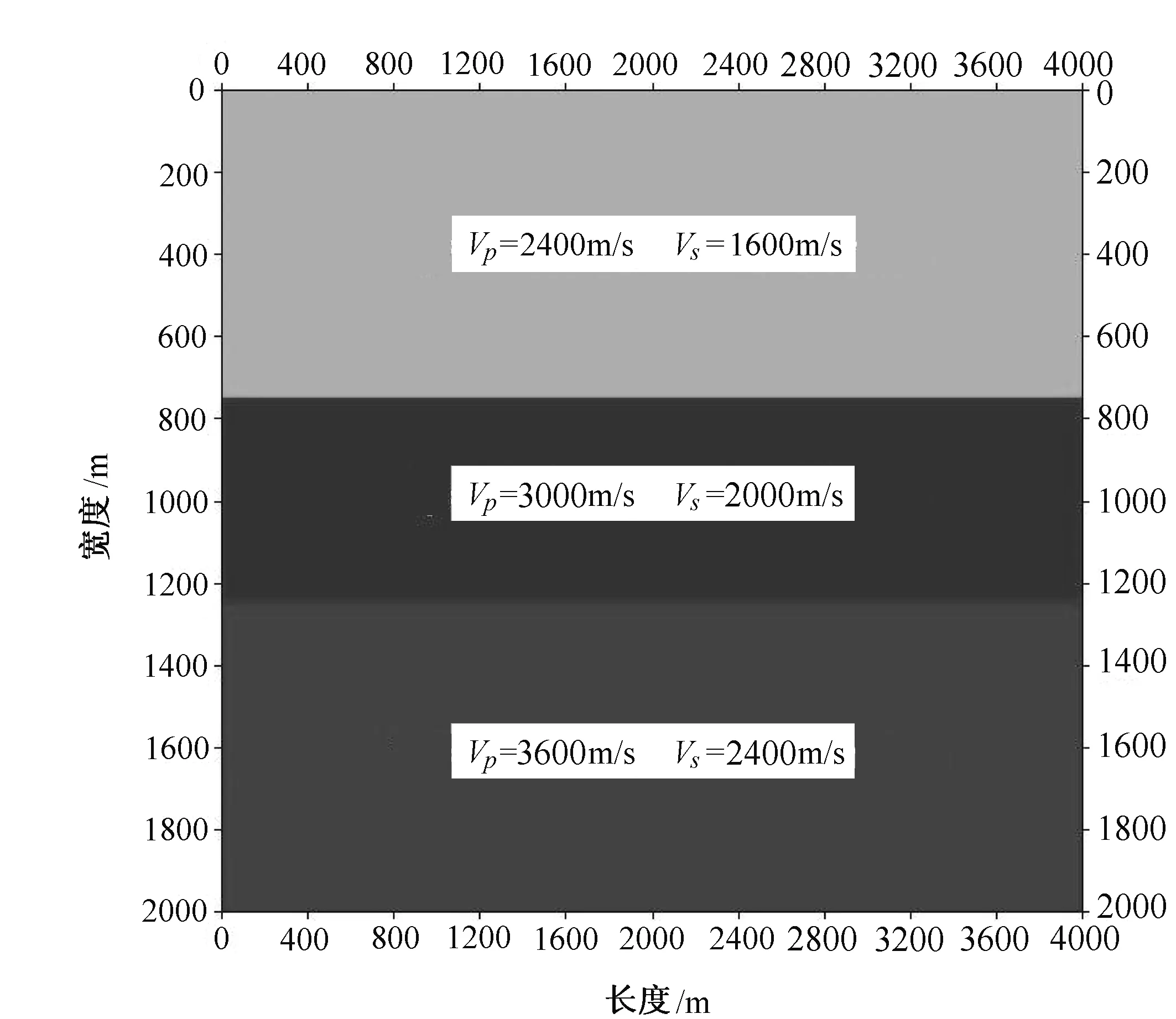
图1 速度模型

以水平层状介质为例，考察分离波场及地面记录效果。速度场大小4000×2000m2，速度值如图1所示，震源位于地表的水平位置中心点。模拟采用10×5m2的速度网格，方程求解同样采用时间2阶、空间8阶有限差分。图2展示了分离前后的瞬时波场，可以发现，波场分离后，纵波波场相对单一，即除直达P波外即为PP波(含极弱的SP转换波)，而横波波场除直达S波和PS转换波外，还包含SS波。

图3展示了地面接收到的X、Z分量及分离后的P、S波记录，分离后的P波记录为标量，而横波记录的矢量性质，造就了震源两侧记录极性反向的特性，而这一特性与野外采集的横波数据恰恰吻合，因此，采用求取旋度的方式分离弹性波场中的横波波场，为转换横波的模拟在物理特性方面提供了便利条件。

图2 水平层状弹性介质中瞬时波场分离

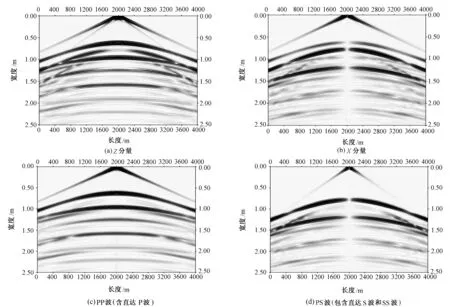
图3 水平层状弹性介质波场模拟及分离的地表记录

3 结 论

从弹性波场的散度和旋度的求取入手，利用引入的等价方程论证了纵波的无旋及横波的无散理论，通过理论推导及模型试算，得出以下结论：

1)在满足差分范围内速度无剧烈变化的情况下，通过分别求取波场的散度和旋度能有效地分离出纵、横波场。

2)由于散度运算为标量运算，因此分离出的纵波波场为单一的标量场。

3)旋度运算的矢量性质造就了分离后的记录在震源两侧极性反向的特性，而这一特性与野外采集的横波数据恰恰吻合。因此，采用求取旋度的方式分离弹性波场中的横波波场，为转换横波的模拟在物理特性方面提供了便利条件。

[1]Dankbaar J W M.Separation of P-waves and S-waves[J].Geophysical Prospecting, 1985, 33:970～986.

[2]Devaney A J, Oristaglio M L.A plane-wave decomposition for elastic wave fields applied to the separation of P-waves and S-waves in vector seismic data[J].Geophysics,1986,51:419～423.

[3]Dellinger J,Etnen J.Wave-field separation in two-dimension anisotropic media[J].Geophysics, 1990, 55: 914～919.

[编辑] 洪云飞

P631

A

1673-1409(2010)01-N051-04