美式期权定价的一个非线性偏微分方程

陈耀辉

(南京财经大学经济学院，江苏 南京 210046)

孙春燕

(南京财经大学应用数学学院，江苏 南京 210046)

美式期权定价的一个非线性偏微分方程

陈耀辉

(南京财经大学经济学院，江苏 南京 210046)

孙春燕

(南京财经大学应用数学学院，江苏 南京 210046)

在最优停时理论中，利用动态规划原则，得到了关于美式(看涨或看跌)期权定价的一个非线性Black-Scholes型偏微分方程，利用粘性解的概念证明了该偏微分方程的解的存在性和唯一性，由此得到了美式期权定价的一个新方法。

美式期权定价；动态规划原则；非线性Black-Scholes型偏微分方程；粘性解

与欧式期权定价存在解析表达式相反，美式期权定价是没有显式解的，美式期权的无套利定价是最优停时问题的解[1，2]。简单地说，最优停时问题的解可以通过2个主要的方法确定：一是基于拟变分不等式公式[3～5]，二是基于自由边界问题公式[6，7]。这2种方法都必须使用数值算法来确定美式期权价格，其优点和不足见文献[8]。

下面，笔者提出了关于美式期权定价问题的一个微分公式，在这个新的公式中，将要寻找一个函数v=v(t,x)满足v(T,x)=g(x)和Black-Scholes类的非线性偏微分方程：

(1)

式中，x≥0，t∈[0,T)；r，d，σ为给定的常数；并且非线性项q是如下的形式：

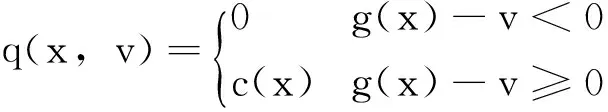
(2)

式中，“现金流”函数c(x)按下式定义：

(3)

1 美式期权定价理论

假设股息支付股票的价格动态X(s)=Xl,x(s)是由几何布朗运动(在等价鞅测度Q下)决定，即它按照下列随机微分方程发展变化：

dX(s)=(r-d)X(s)ds+σX(s)dW(s)s∈(t,T]

(4)

其中，d≥0是股票的确定股息；r≥0是无风险利率；σgt;0是波动度； {W(s)|s∈[0,T]}是一个标准布朗运动；T是期权合约的执行时间，具有初始条件X(t)=x。因此，一个美式期权的无套利定价是：

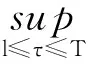
(5)

其中，上确界是对停时τ∈[t,T]而言；El,x表示在等价鞅测度Q条件X(t)=x下的期望。笔者将讨论支付函数g:R→R:

(6)

式中，Kgt;0是合约的执行价。

称式(5)所定义的V(t,x)是最优停时问题的值函数。∀ε≥0，若下列动态规划原则[9]成立：

(7)

则τε将是一个ε-最优停时，对任意停时t≤θ≤τε:

V(t,x)=El,x[e-r(θ-t)V(θ,X(θ))]

(8)

选择ε=0，则τ0是一个最优停时，且过程：

M(s)=e-r(s-t)V(s,Xl,x(s))t≤s≤τ0

(9)

是一个鞅。由式(8)可以推出下列关于最优停时问题的动态规划原则[10]：

对任意停时θ∈[t,T]，有:

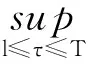
(10)

选择τ=T，对任意停时θ∈[t,T]有：

V(t,x)≥El,x[e-r(θ-l)V(θ,X(θ))]

(11)

注：若选择τ=t，则有V(t,x)≥g(x)(称为早期执行合约)。

式(5)定义的价值函数V(即美式期权定价)可通过上述2种方法得到[3,4，6,8,11]。为了以后讨论的方便，在此给出价值函数V的一个重要性质。

证明由文献[12]知V是连续的，V的上界和下界可以利用0≤g(x)≤K(对于看涨期权)和0≤g(x)≤x(对于看跌期权)导出。

2 粘性解的存在性与唯一性

下面讨论具有终值条件：

V(T,x)=g(x)x∈[0,∞)

(12)

的非线性Black-Scholes方程：

LBSV(t,x)-rV(t,x)=-q(x,v(t,x)) (t,x)∈QT

(13)

该终端定价问题的解构造了美式期权定价问题的一个新的公式。

2.1粘性解的相关概念

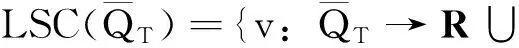
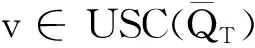
(14)

另外，在[0,∞)上，如果v|l=T≤g，则v是终值问题式(13)的一个粘性下解。

另外，在[0,∞)上，如果v|l=T≥g，则v是终值问题式(13)的一个粘性上解。

引理1假设xgt;0时，v是式(13)的一个下解(上解)，则当x≥0时，v也是式(13)的一个下解(上解)。

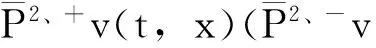
并且在(t,x)处，v-φ有一个最大值(最小值)[13]。所以有下面基于半射流的上下解的等价定义：

2.2存在性与唯一性

为证明粘性解唯一性的需要，下面直接引入半连续函数的最大值原则：

a≤C，如果(a,p,X)∈P2、+v(t,x)，|x-xφ|+|t-tφ|≤ρ，|v(t,x)|+|p|+|x|≤M

则∀Kgt;0，存在实数aφ,bφ∈R和2阶矩阵Xφ,Yφ使得：

并且aφ-bφ=∂lφ(tφ,xφ,yφ),对称的2阶矩阵A的范数定义为：

‖A‖=sup{|lt;Aξ,ξgt;||ξ∈R2,|ξ|≤1}

这里对看涨期权来说C1=0且C2=1，对看跌期权来说C1=K且C2=0。该解v与美式期权定价V相一致。

定理1的证明分2步进行，第1步(定理2)，证明美式期权定价式(5)是终值问题式(13)的一个粘性解，由此提供了存在性的结果。第2步(定理3)，证明一个关于上下解的比较原则，它暗示粘性解的唯一性。

2.2.1存在性

引理3式(6)定义的支付函数g是式(13)的一个下解。

证明只考虑看涨期权g(x)=(x-K)+的情形(看跌期权证法类似)。分下列5种情形来考虑：

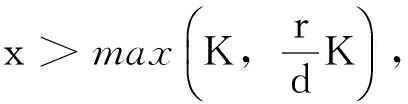
LBSg(x)-rg(x)+q*(x,g(x))=0

LBSg(x)-rg(x)+q*(x,g(x))=0

LBSg(x)-rg(x)+q*(x,g(x))=0

LBSg(x)-rg(x)+q*(x,g(x))=dx-rK≥0

定理2式(5)定义的价值函数V(t,x)是终值问题式(13)的一个粘性解。

证明通过对式(5)的检验，V显然满足终值条件(12)。由此和性质1，下面只须证明V既是非线性Black-Scholes方程式(13)的一个下解也是上解。

LBSφ(t,x)-rV(t,x)=LBSφ(t,x)-rφ(t,x)≤0

LBSφ(t,x)-rV(t,x)≥0

LBSφ(t,x)-rV(t,x)+q*(x,V(t,x))≥0

这就得出下解性质的证明，定理2证毕。

2.2.2唯一性

(15)

进一步，假设存在一个有限常数C使得：

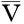
(16)

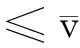
(17)

故终值问题式(13)至多存在一个粘性解v(t,x)，它是递增的且至多在x处是线性的(当x→∞ )。

(18)

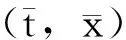
Φ(t,x,y)中惩罚函数Ψ(x,y)构造如下：

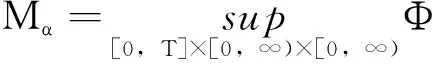
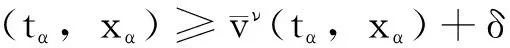
(19)

∀αgt;1和足够小的ε，利用Φ(T,0,0)≤Φ(tα,xα,yα)和(16)，则有：

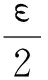
这就表示存在一个有限常数Cε(依赖于ε)使得xα,yα≤Cε。由此得到存在一个序列，仍记为(tα,xα,yα)，它收敛于(tε,xε,yε)∈[0,T]×[0,∞)×[0,∞)，当α→∞(对每个固定的ε)，由文献[7]得到最大值点(tα,xα,yα)满足：

考虑一种特殊的情形tε=T，注意到：

(20)

根据粘性上下解的定义有：

(21)

其中:

更进一步，在文献[7]的基础上使用式(20)便有：

根据H*和H*可能值的检验，可看出：

-C(yα)≤E4(α)≤max(0,C(xα)-C(yα))

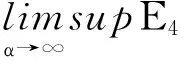
如果λ选择足够大，上述不等式总是成立，与式(18)矛盾，故定理3成立。

[1]Bensoussan A.On the theory of option pricing[J]. Acta Appl Math，1984，2(2):139～158.

[2]Karatzas I.On the pricing of American options[J]. Appl Math Optim，1988，17(1):37～60.

[3]Bensoussan A，Lions J L.Applications of variational inequalities in stochastic control[M]. Amsterdam: North-Holland Publishing Co, 1982.

[4]Bensoussan A, Lions J L.Impulse control and quasivariational inequalities[M].Montrouge: Gauthier-Villars, 1984.

[5]Jaillet P, Lamberton D， Lapeyre B.Variational inequalities and the pricing of American options[J].Acta Appl Math，1990，21(3):263～289.

[6]McKean Jr H P.Appendix: a free boundary problem for the heat equation arising from a problem in mathematical economics[J]. Indust Manage Rev，1965，(6):32～39.

[7]Crandall M G， Ishii H， Lions P L. User’s guide to viscosity solutions of second order partial differential equations[J]. Bull Amer Math Soc(N.S.) ，1992，27(1):1～67.

[8]Myneni R.The pricing of the American option[J]. Ann Appl Probab，1992，2(1):1～23.

[9]Shiryayev A N. Optimal stopping rules[M]. New York: Springer, 1978.

[10] Krylov N V. Controlled diffusion processes[M]. New York: Springer, 1980.

[11]Van Moerbeke P.On optimal stopping and free boundary problems[J]. Arch Rational Mech Anal，1975-1976，60(2):101～148.

[12] Karatzas I, Shreve S E. Methods of mathematical finance[M]. New York: Springer, 1998.

[13]Fleming W H, Soner H M.Controlled Markov processes and viscosity solutions[M]. New York: Springer, 1993.

[编辑] 洪云飞

O211.9

A

1673-1409(2010)01-N011-06