主内射模的一个注记

李炳君,谭淑芬,邓华

(湖南人文科技学院数学与应用数学系,湖南娄底 417001)

主内射模的一个注记

李炳君,谭淑芬,邓华

(湖南人文科技学院数学与应用数学系,湖南娄底 417001)

如果 R的任意主理想 I到M的 R-模同态都可以扩充为 R到M的同态,则称 R-模M为主内射模 (或者 P-内射模)。通过进一步研究 P-内射模的性质,得出 P-内射环的全矩阵环Mn(R)仍然是 P-内射环的充分必要条件。

P-内射模;P-内射环;全矩阵环

1 前言

内射模是模论和同调代数理论中重要的模类。它可以看作投射模的对偶,对确定环的同调性质和计算同调不变量也十分重要,因此具有深刻的研究背景。由于内射模的内部结构至今不被人们所掌握,因此对内射模及其性质的深入研究就自然成了模论里的重要研究课题之一。在对内射模的推广得到新的模类的研究过程中,人们通常可以更深刻地认识内射模的内在结构,并且还能对许多重要的环类从模的角度进行刻画。

在文 [1]中,Nichoson和 Yousif定义了主内射模 (以下简称 P-内射模):若 R的任意右主理想 I到M的模同态都可以扩充为 R到M的同态,则称右 R-模M称为右主内射模。如果右正则模 RR是 P-内射模,则称 R是右主内射环。在文[2]中,相同的作者又定义了极小内射模,给出了极小内射环一些很好的刻画,并推广了 Farkas关于群环RG的结果,同时他们还研究了极小内射环的结构。在文[3]中,Stanleys和 Yiqiang Zhou推广了主内射环的概念,定义了 AP-内射环、GAP-内射环和 QAP-内射环,并对它们的性质进行了研究。

本文进一步研究了 P-内射模的性质,得到了 Homs(R,E)为 P-内射左 R模的一个充分条件。若 R的任意 n个元素生成的右理想 I和模同态α:I→M都能扩张成模同态β:R→M,则称称 R-模 M是右 n-内射的。文 [3]证明了若 Mn(R)是右 P-内射的,则 R是右 n-内射的。以上得到的是全矩阵环Mn(R)是右 P-内射的一个必要条件,这引发了我们对Mn(R)是右 P-内射环的充分必要条件的思考。

我们称环 R为右 F-内射环,如果对 Rn的任意有限生成 R-子模 M,和右 R-同态 f:M →R,都可以扩张到 f′:Rn→R。其中 Rn={(r1,…,rn)T|r1,…,rn∈R}。我们证明了一个全矩阵环Mn(R)是右 P-内射环的充分必要条件是环 R是右 F-内射环。本文中所讨论的环都是指有单位元的结合环,模都是指酉模,其他未加说明的概念和术语请参见 [4]、[5]。

2 主要结果

我们有一个由内射 Abel群得到内射 R-模的方法:对任意的内射 Z-模 E和对任意的环 R,Homz(R,E)是内射R-模 (这里 R看作 Z—R双模)。而且我们有更一般的结果,把 Z换成任一交换环 S,R改成 S-代数 (R为左 S模,R是环,且满足:s(rr1)=s(r)r1=r(sr1),∀ r,r1∈R,s∈ S)。

引理 2.1[4]设 E为内射 S-模,S为交换环,R为 S-代数,则 Homs(R,E)为内射左 R模。

对于 P-内射模,我们有如下结论:

定理 2.2 设 E为 P-内射 S-模,S为交换环,R为 S-代数 ,则 Homs(R,E)为 P-内射左 R模。

证明:R的任一左主理想 Ra令 i∈Hom(Ra,R)为嵌入同态,只需证明:任意的 f∈HomR(Ra,Homs(R,E))可以拓广到 f′∈HomR(R,Homs(R,E))。因为 E是 S—S双模,R是右 S模,且 R-模同态 f,i也是 S-模同态,我们作交换图 1:

定义φ∈Homs(Homs(R,S),E),使

由于 E是内射的 S-模,必有 g∈Homs(R,E)使得 gi=φf。定义 f′∈HomR(R,Homs(R,E))使

图1 交换图

首先证明 f′∈HomR(R,Homs(R,E)):任取 r,r1,r2∈R,则

由 r的任意性得 f′(r2r1)=r2f′(r1),从而

f′∈HomR(R,Homs(R,E)).

再证 f′i=f,任取 x∈ I,则 f′i(x),f(x) ∈Homs(R,E).由于

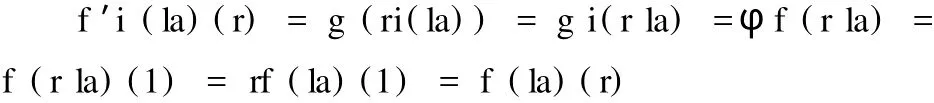
故

从而完成了我们的证明。

定理 2.3 对 ∀ n≥1,若 anR是 P-内射右 R-模,则anR⊕R.

证明:定义 R-同态

而 anR是 P-内射的,故存在 anr1,使

故 f(an) =anr1an=an.令 anr1=e,则

又 anR=eR,因此,anR是 RR的直和项。

称 R-模M是右 n-内射的,若 R的任意 n个元素生成的右理想 I和模同态α:I→Μ都能扩张成模同态β:R→Μ 。若 R是一个环,Mn(R)表示 R的 n阶全矩阵环 Mn(R)是右 P-内射环的一个必要条件,这引发了我们对其充要条件的思考。为此,我们要引入一个新的定义:

定义 2.4 环 R称为右 F-内射环,如果对 Rn的任意有限生成 R-子模M,和右 R-同态 f:M →R都可以扩张成 f′:Rn→R,其中 Rn={(r1,…,rn)T|r1,…,rn∈R}。我们有以下定理:

定理 2.5 对任环 R,下列两条等价:

(1)环 R是右 F-内射环,

(2)Mn(R)是右 P-内射环。

证明:(1)⇒ (2) 设 ∀A∈Mn(R),则 A Mn(R)为Mn(R)的任一右理想。又设

φ:A Mn(R)→Mn(R)

为一右 Mn(R)-同态,令

A= (α1,α2,…,αn)

其中αi表示矩阵 A的第 i列,令

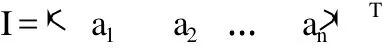
其中 aj(j=1,2,…,n)表示A在φ下的像φ(A)的第j行。若η∈Rn且Aη=0, 则ajη=0,故r Rn(A)⊆r Rn(aj)又 A Rn= ∑ni=1αiR是有限生成 R-子模。

定义:

由上面的讨论容易证明 fj是定义良好的 R-同态。

由 (1),fj可以扩充到 gj:(Rn)R→RR。因此,对任意η∈Rn

其中 e1,e2,…,en表示 Rn的标准基向量。

因此

令

则f(A)=D·A.

D = (dij)= (gj(ej))∈Mn(R)(2)⇒(1)设Rn中任意 m个元α1,α2,…αm,令

f:M→R

是任一 R-同态。由线性代数的知识,我们这里不妨假设 m=n,又设

则对任意的ξ∈Rn,f(Aξ)=η ξ.

由[1,Proposition 1],Mn(R)B⊆Mn(R)A,故存在 C

∈Mn(R),使得 B=CA,其中

从而η =c1A, 故?j∈1,2,…,n, f(αj)=ciαj.即f可以表示成Rn中某一个元素的转置c1的左乘,令

c1i表示行向量 c1的第 i个元素,易见 g:Rn→R是一个 R-态射,且 g是 f的扩张,从而环 R是右 F-内射环。

[1]NICHOLSON W K,YOUSIFM F.Principally injective rings[J].Algebra,1995,174(1):77-93.

[2]NICHOLSON W W K,YOUSIFM F.Mininjective rings[J].Algebra,1997,187(2):548-578.

[3]STANLEY S P,ZHOU Yiqiang.Generalizations of principally injective rings[J].Algebra,1998,206(2):706-721.

[4]佟文廷.同调代数引论 [M].北京:北京高等教育出版社,1998:125-129.

[5]F.W.Anderson,K.R.Fuller.Rings and Categoriesof Modules[M].New York:Springer-Verlag,1974:10-26.

(责任编校:光明)

A Note on Principally I njectiveModules

LI B ing-jun,TAN Shu-fen,DENG Hua

(Department ofMaths and ApplicationMaths,Hunan Institute of Humanities,Science and Technology,Loudi,417001,China)

An R-moduleM is said to be principally injective(P-injective)if every rightR-homomorphism from anyprincipal ideal Iof R intoM can be extended to R.In this note,we study the propertiesof P-injectivemodules and get a condition underwhich matrix ringMn(R)of a P-injective ring R is again a P-injective ring.

P-injective module;P-injective ring;matrix ring

O153.3

A

1673-0712(2010)02-0003-02

2010-01-16.

湖南省教育厅科学研究项目(09C542);湖南人文科技学院引进人才科研启动项目.

李炳君 (1981-),男,湖南株洲人,湖南人文科技学院数学与应用数学系讲师,博士,研究方向:同调代数。

[收稿日期 ]2010-02-20.

[作者简介 ]高玉泉 (1962-),男,湖南涟源人,湖南人文科技学院教育科学系教授,研究方向:宏观经济学、实践教学与人才培养。