基于模糊时间序列模型的股票市场预测

蔺玉佩，杨一文

(西北工业大学 管理学院，西安 710129)

0 引言

股票价格序列预测不仅对投资者而言有巨大的市场利益，同时对学术界研究市场运行规律无疑也具有重要的理论价值。因此研究采用何种方法对股票价格进行较准确的预测就成为是国内外学者都非常关注的课题。时间序列预测方法是常用的股票价格预测方法。一般的时间序列预测方法，如ARIMA等，都是以时间序列的精确值为基础并且认为时间序列的未来值与当前值、过去值以及白噪声之间存在着确定、明确的函数关系。但是，证券市场系统非常复杂，市场的行为特征是不明确的，精确的记录往往会丢失部分有用的信息，许多变量之间的关系也难以用确定的函数关系来描述。因此，本文将模糊时间序列模型用于股票指数价格的预测，将观测值表示为具有模糊特征的语言变量并且建立了多前件的模糊关系，最后通过去模糊化得到精确值。结果表明此法更能全面反映系统的特征并且有利于复杂环境中提高预测精度。

1 模糊时间序列与模糊逻辑关系

本文应用模糊时间序列模型对上证综指和深证成指进行预测，首先对模糊时间序列的定义作一简要叙述。

令U为给定论域，将论域划分为n个子区间，则U={u1,u2，…,un}。一个定义在论域U中的模糊集合A表示如下：

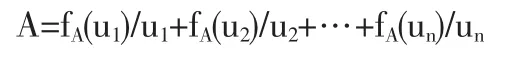
其中，fA(·)是 ui对模糊集合 A 的隶属函数，fA(ui)是 ui对模糊集合 A 的隶属度，fA(ui)∈[0,1]，i=1,2,…,n。

定义1 令R中一子集Y(t)(t=…,0,1,2,…)为给定论域，fi(t)(i=1,2,…)为定义在其上的模糊集合，由 f1(t)，f2(t)(组成的集合F(t)称作定义在Y(t)(t=…,0,1,2,…)上的模糊时间序列。

定义 2 如果 F(t)仅仅由 F(t-1)引起，即 F(t-1)→F(t)，这个关系可表示为F(t)=F(t-1)°R(t,t-1)，称F(t)作的一阶模型，R(t,t-1)为F(t-1)与F(t)之间的模糊关系。

定义2中，F(t-1)为模糊关系的前件，F(t)为后件，此关系式是具有单个前件的一阶模糊关系式。

定义3 F(t)为给定论域上的模糊时间序列，如果F(t)同时由F(t-1),F(t-2),…,F(t-n)引起，则n阶模糊逻辑关系可表示为 F(t-n)、…、F(t-2)、F(t-1)→F(t)，其中 F(t-n)、…、F(t-2)、F(t-1)为n阶模糊逻辑关系的当前状态。

定义4 假设R中一子集Y(t)(t=…,0,1,2,…)为给定论域，F1(t),F2(t),…,Fn(t)是各自给定论域上的n个模糊时间序列，如果 F(t)同时由 F1(t),F2(t-1),F3(t-1),…,Fn(t-1)引起，具有 n个前件的一阶模糊关系可表示为Fn(t-1),…,F2(t-1),F1(t-1)→F(t)。

综合以上定义，具有n个前件的n阶模糊逻辑关系式可定义如下：

定义5 F1(t),F2(t),…,Fn(t)和F(t)为各自给定论域上的n+1个模糊时间序列，则具有n个前件的n阶模糊逻辑关系式可表示为：(F1(t-n),F2(t-n),…,Fn(t-n))、…、(F1(t-2),F2(t-2),…,Fn(t-2))、(F1(t-1),F2(t-1),…,Fn(t-1))→F(t)。

2 模糊时间序列预测模型

本文建立的模糊时间序列模型主要包括以下步骤：模糊化、建立模糊关系、预测并去模糊化。

步骤1 模糊化

定义论域 U。 论域 U=[Dmin-σ，Dmax+σ]，其中 Dmin和 Dmax分别为训练样本数据中的最小值和最大值，σ为训练样本标准差。采用模糊C-均值聚类算法将数据聚类，并根据聚类结果论域划分为多个子区间，首先计算聚类数k，则

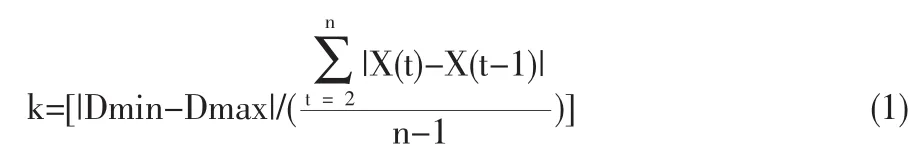
其中，n为训练样本个数，Dmin和Dmax分别为训练样本序列中的最大值和最小值，X(t)和X(t-1)分别为t时刻和t-1时刻的训练样本的观测值。[]为四舍五入取整运算。其次通过模糊C-均值聚类算法将数据分为k类，相应地得到k个聚类中心ji(i=1,2,…,k)。将相邻两个聚类中心的中点做为论域子区间的边界点，定义边界点为di(i=1,2,…,k-1)。划出k个子区间：(Dmin,d1)、(d1,d2)、(d2,d3)、…、(dk-1,Dmax)，分别用 u1、u2、…、uk表示。可以看出，各子区间长度各异，这是因为样本数据在其论域上的分布不是均匀的，而是有其复杂的内部结构，用聚类结果来指导子区间的划分显然比等分论域能更好地反映数据结构，有利于提高预测精度。

最后定义子区间对应的模糊集合，并将数据模糊化。定义模糊集合Ai为：

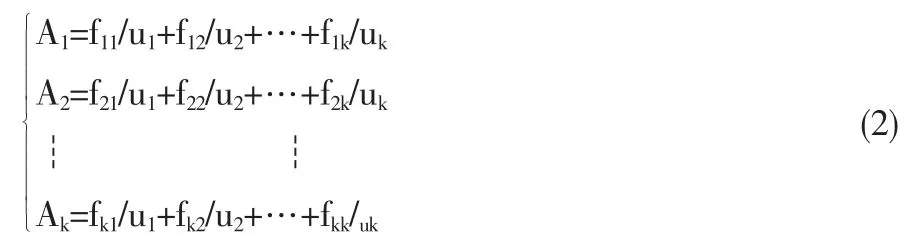
其中，fij表示uj对模糊集合Ai的隶属度(i=1,2,…,k;j=1,2,…,k)。数据的模糊化规则为：如果某样本数据属于ui，且ui对Ai的隶属度在其所有隶属度中是最大值，则可将该数据值模糊化为Ai。将所有样本数据模糊化，得到对应的模糊时间序列。将股票每日收益率、5日移动均线变化值、成交量和DHL四个时间序列分别定义为{R(t)}、{M(t)}、{V(t)}和{D(t)}（t=1,2,…,n），其中n为训练样本数。根据式(1)得出聚类数分别为k1,k2,k3和k4，在各自的论域上将上述4个时间序列模糊化后得到的模糊时间序列分别为 A(t,i)（i=1,2,…,k1），B(t,j)（j=1,2,…,k2），C(t,p)（p=1,2,…,k3）和D(t,q)（q=1,2,…,k4；t=1,2,…,n）。

步骤2 建立模糊关系

选用n天的样本数据作为建模的训练数据，设当天为t，前三天分别为t-3，t-2和t-1，t=1,2,…,n。利用上述模糊时间序列建立具有四前件、三阶模糊关系的模糊时间序列预测模型：

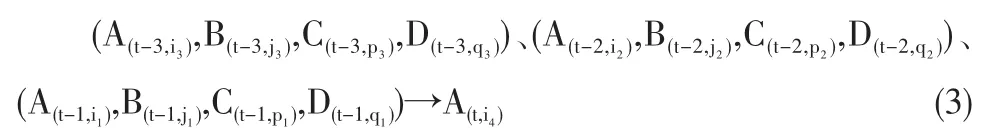
其中 i1,i2,i3,i4=1,2,…,k1；j1,j2,j3=1,2,…,k2；p1,p2,p3=1,2,…,k3；q1,q2,q3=1,2,…,k4。则按时间顺序可以依次建立共计n-3个模糊关系，形成训练数据模糊关系表，如表1所示。

步骤3 预测并去模糊化

(1)预测

预测未来T时刻的模糊收益率A(T,i4)，其模糊逻辑关系式为：

表1 训练数据模糊关系

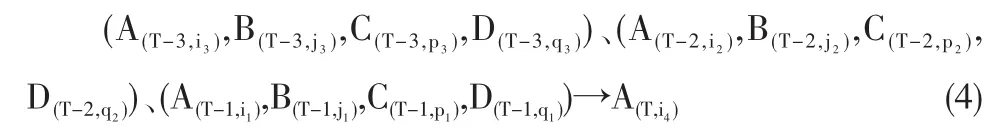
将上式左边的前件依次与表1中列出的n-3个关系式的前件逐个进行对比。具体地，本文提出的对比原则是：计算前件相同位置上第二下标的差值的绝对值，例如，模糊集合A(T-3,i3)中 i3=m3（1≤m3≤k1），A(t-3,i3)中 i3=n3（1≤n3≤k1），则差值绝对值为|m3-n3|，将12对模糊集合第二下标的差值绝对值求和，如果和小于等于某一设定值（如20），则认为关系匹配成功。这样做的优点是整体度量两个模糊关系前件的差异，设定的值越小，差异度量越精确，但匹配成功的次数将随之降低，反之亦然。如果一次预测关系匹配成功的个数为N，则这N个训练数据模糊关系式的后件构成了本次预测结果集合A(·,·)，该集合中模糊集合出现的次数不一定相同，有些可能多次出现，有些则可能仅出现一次。设各可能出现结果值的频数为 fi（i=1,2,…,k1），预测结果集合如表 2所示，集合中的每一个模糊集合对应一个聚类中心。

(2)去模糊化

采用重心法去模糊化。根据表2结果去模糊化得到预测值

3 应用实例

3.1 数据说明

选取上证综合指数和深证成份指数每日收益率、收盘价、最高价、最低价和成交量为样本，区间分别为2005-12-14至2009-4-15和2005-12-26至2009-4-15①数据来源于清华金融研究数据库(http://211.157.28.243/terminal/system/gotoLogin.action)。。收益率采用对数收益率，DHL由最高价、最低价和收盘价计算得到。由于成交量数值比较大，将其单位改为万手。最后得到上证综指有效数据共800天，深证成指共794天。

3.2 预测步骤

依照前文的建模步骤，使用上证指数的数据来说明预测过程。

步骤1 模糊化

取前750个交易日数据作为训练样本，后50个交易日数据用于预测。以上证指数收益率的模糊化过程为例。

表2 一次模糊预测所有可能的结果

首先定义论域U。收益率训练样本中最大值和最小值分别为 0.0903 和-0.0926，σ=0.0258。 得到 U=[-0.1184,0.1161]。由于市场实施10%的涨跌幅限制，在[-0.1,0.1]范围以外没有值，所以我们定义收益率论域U=[-0.1,0.1]。

其次划分子区间。根据式(1)可得分类数k1=10，使用matlab模糊逻辑工具箱函数中的模糊C-均值聚类函数fcm将训练数据进行分类，得到10个聚类中心分别为：-0.0789,-0.0483,-0.03,-0.0181,-0.0067,0.0015,0.0089,0.0167,0.0267,0.0446，以相邻两个聚类中心中点作为子区间的分界点，将论域划分成10个子区间分别为u1=[-0.1,-0.0636),u2=[-0.0636,-0.0392),u3=[-0.0392,-0.024),u4=[-0.024,-0.0124),u5=[-0.024,-0.0026),u6=[-0.0026,0.0052),u7=[0.0052,0.0128),u8=[0.0128,0.0217),u9=[0.0217,0.0356),u10=[0.0356,0.1]。

再根据式(2)定义模糊集合为：

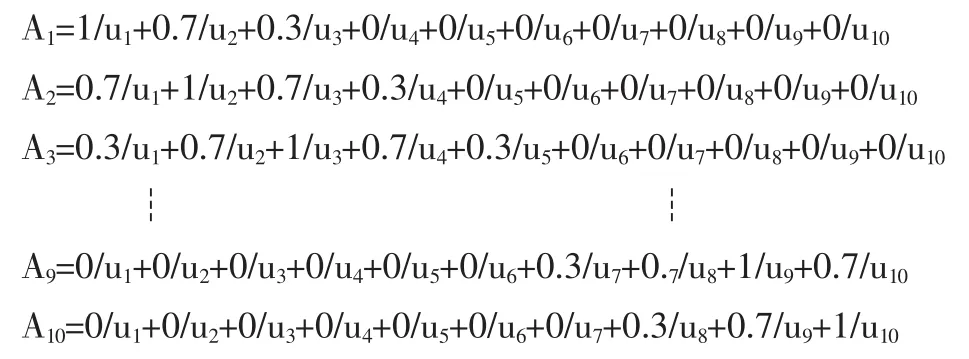
最后将数据模糊化。例如，2006-11-17的收益率为0.0155，它落在区间u8内，u8对于A8的隶属度在所有区间中最大，所以将0.0155模糊化为A8。将收益序列中所有数据模糊化后可得对数收益率的模糊时间序列。同样方法将其它三个序列的数据在各自论域上模糊化为模糊时间序列。

步骤2 建立模糊关系

利用750日的训练数据可构造747（=750-3）个模糊关系如表3所示，然后将预测T日的模糊关系式(5)中的前件与这747个模糊关系的前件进行比对，选出匹配成功的模糊关系。需要指出的是，为了书写简洁，又不致产生歧义，后文中省略了模糊时间序列中模糊集合的第一个（时序）下标。

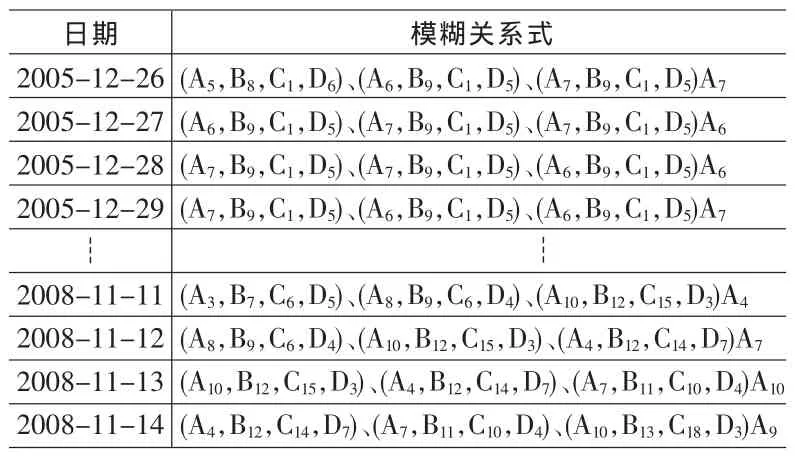
表3 上证指数训练数据模糊关系

步骤3 预测并去模糊化

(1)预测

以2009-2-4这一天为例说明预测过程。当日收益率为Ar。用前3天历史数据并根据式(5)可建立模糊逻辑关系式为：

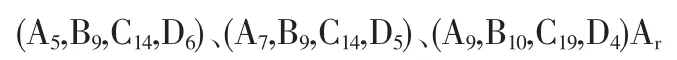
将其前件中的模糊集合与表3中各关系式前件中对应的模糊集合根据对比原则进行一一对比，最后匹配成功的关系式个数为58个，这58个模糊关系式的后件构成了预测结果集合如表4所示。

表4 上证指数2009-2-4模糊预测结果

(2)去模糊化

根据公式(4)可以得出2009-2-4日的收益率预测结果为0.00142239。当天的实际收益率为0.023。

4 预测结果分析

对上证指数和深证指数从2009-2-4至2009-4-15的50天价格的预测结果如图1、图2和表5所示。为客观评价本文提出的模糊时间序列模型的预测效果，我们特意将其与模糊时间序列中的标志模型进行对比，结果如表5所示。

由表5（第2、4列）可以看出，对于同样两市指数的50日预测，Chen的模型[4]的平均预测误差接近或高于2.5% ，而本文建立的模型的平均预测误差都明显低于2%，预测结果的改进还是很明显的。同时也说明本文在论域划分以及模型变量的选择方面所作的努力还是有一定成效的，同时也表明，对于处理复杂问题的模糊时间序列而言，在论域划分和模型变量选择应予以高度重视。

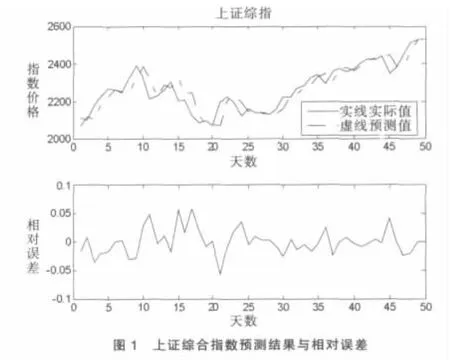
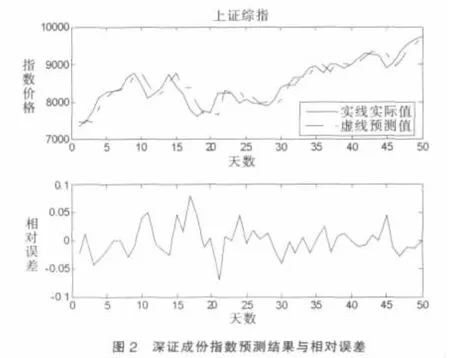
价格指数数值的预测固然重要，但是退一步，其未来的变化趋势即涨跌无疑也是非常重要的信息。应用本文建立的模糊时间序列模型分别对上证指数、深证指数未来涨跌趋势进行预测，预测区间：2009-2-4至2009-2-24。预测的过程同上，只是省了去模糊化这一步骤，直接在论域上找出预测得到的模糊集合（后件）所对应的子区间ui(i=1,2,…,k1)，进而判断指数变动趋势。同样地，我们也将其与Chen的模型进行了对比，结果如表5（第3、5列）所示。Chen的模型对两市指数的趋势预测正确率均低于60%，而本文模型的预测正确率分别接近或高于70%。

5 结论

本文将时间序列分析与模糊规则结合起来所产生的模糊时间序列模型具有两者的优点，是时间序列分析方法的拓展，将其应用于股票价格的预测是一种有益的尝试。

模糊时间序列模型的预测精度主要取决于两点：论域的子区间划分和模糊关系的建立。前者要求合理划分论域，反映真实的数据分布结构，并以此为基础选择适当的去模糊化方法；后者则要求不仅对数据的拟合精度高，而且还要求模型具有较好的推广能力，为达到这一目的，必须选择适当的模型变量，即前件变量，同时还要建立有效的模糊规则。因此本文选择模糊聚类方法实现对论域的子区间划分，力求客观地反映样本数据的结构分布，并为划分论域提供一个比较客观的方法。相应地，采用重心法区模糊化，实现对收益的精确预测。影响价格的因素很多，但模型中又不可能引入过多的变量，否则不仅导致运算量过大，而且使模糊关系过于复杂，使模型的推广能力下降。基于上述考虑，本文选择历史收益率、5日移动平均线、成交量以及多空双方强弱对比4个变量作为模型的变量，建立了多前件的模糊时间序列模型，并特别设计了能反映多空双方力量对比的指标DHL以及模糊规则的确定原则。预测结果表明，本文建立的模糊时间序列模型较典型的模糊时间序列模型具有较高的预测精度。

表5 上证、深证指数预测误差

由于所面临问题的复杂性，模糊时间序列模型的运用是问题导向的。即论域的划分、模糊关系的建立必须根据具体问题设计合理的方法，这些方面仍有许多工作要做。例如模糊关系前件比对过程中，本文选择的20这一数值仅仅是经过累试后得到的，工作量比较大；另外，论域的划分与模糊规则的建立目前还是独立的两部分内容，如果将二者联合起来综合考虑，对提高模型精度无疑具有重要意义。

[1]Song,Q.,Chissom,B.S.Fuzzy Time Series and Its Models[J].Fuzzy Sets and Systems,1993,（54）.

[2]Song,Q.,Chissom,B.S.Forecasting Enrollments with Fuzzy Time series-Part I[J].Fuzzy Sets and Systems,1993,（54）.

[3]吴铭锋，蒋勋.基于模糊时间序列的预测模型-以上证指数为例[J].价值工程，2008，(11).

[4]何云峰，杨燕.基于模糊时间序列-股票走势的建模与应用[J].微计算机信息，2006,(33).

[5]张智星，孙春在.神经-模糊和软计算[M].西安：西安交通大学出版社，2000.