一个具有随机扰动项的动态学习模型的构建

周 敏，闫 磊

（中国矿业大学 管理学院，江苏 徐州 221116）

0 前言

由于在系统的演化发展过程中存在学习决策行为的复杂性和动态性，普通的博弈论的纳什均衡不能很好的解决这些问题。但是在符合学习模型的各种基本假设的条件下，我们可以构造一个具有随机扰动项的动态学习模型，它可以把决策行为进行概率化来解决演化过程的复杂性和动态性特征。当系统的演化结果出现稳定解时，我们可以得到具有动态性和复杂性的学习模型的的稳态决策概率分布，这种非确定性纳什均衡解可以看做普通博弈论中的纳什均衡解的扩展。

1 动态学习模型的构建

由于企业的任何决策都是根据以前的决策行为和决策效果决定的，所以的企业的新的决策会随着以前决策行为的结果做出调整，并且总是朝着更好的收益的方向转移。所以说企业的连续决策是具有学习能力的，并且的动态复杂的。我们可以用一个带有漂移的随机分方程来表示这个决策过程。假设企业在原来的基础上根据前一个决策的效果做出新的决策，这个新的决策行为由于受到噪音的影响会发生随机游走产生某种变异。在任一时刻t，系统的状态由t时刻决策的概率分布表示。这样，如果决策状态稳定，决策行为经过演化而得出的结果是一个在稳态下的概率分布。

企业的生产经营行为就是不断的做出决策的行为。在构建的模型中，假设存在m个企业，他们独立的进行连续决策，同时又受到竞争对手以及自己的决策行为和结果的影响。企业的决策行为用ωj(t)∈[c,d]表示，其中t代表决策时间，j代表决策企业。由于随机扰动的的存在，企业的决策行为以某种概率分布的形式来表示。设Gj(ω,t)为表示企业j决策行为的概率分布函数，则其密度函数为：

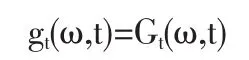
设m-1维向量ωm-1(t)为与决策行为j对应的其它m-1个企业的决策，Gm-1(ωm-1,t)为相应的为m-1个企业的决策行动的概率分布。由于在学习模型中决策行为的学习能力，企业j的收益是由其自身的决策行为和其它的m-1个企业共同决定的。我们用L(s)表示去在t时刻的收益，那么：

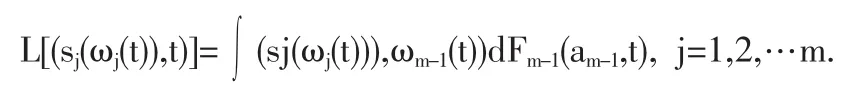
由于任何企业都是以收益最大化为目的的，企业在决策过程中总是调整决策行为可以给自己带来更高收益的决策方向靠拢。同时在决策过程中企业会受到各种噪音的干扰总会出现某些失误，这可以用随机扰动项来表示。

我们将上述的两个过程用如下方程表达出来：

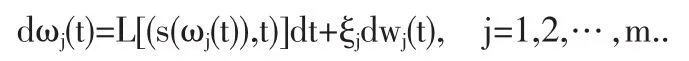
等式右边的第一项为新决策行为对旧的决策行为的调整量。第二项为可能导致决策行为失误的噪声干扰，概率为ξj,wj(t)，为标准维纳过程，wj(t)服从均值为0方差为dt的正态分布。因此：

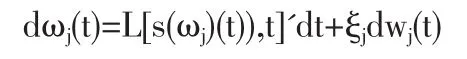
考察到时间间隔，上式可化为：

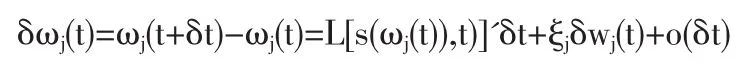
其中 0(δt)为 δt的高阶无穷小。

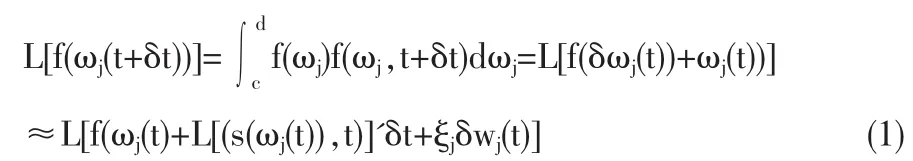
引入任意函数f(ωj)，考察该函数在δt时间间隔后的期望值：我们令 x=ξjδwj(t)的密度函数为 φ(x)，由于 E(x)≈0,E(x2)=ξj2δt，则：

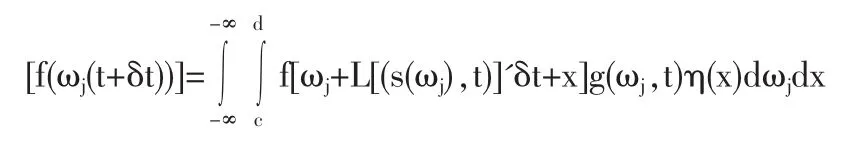
上式描述了具有动态学习行为的企业连续决策行为的系统演化过程。我们可以从中得出下面的结论：

首先，右边第一项-L[(sj(ωj)，t)]'gj(ωj，t)表明，企业的决策行为总是向着可以带来更高收益的方向调整，并且预期收益和现在收益的差距越大调整的速度越快;决策调整速度与企业在t时刻采取行动ωj的概率密度成正比。

我们对上面的式子进一步研究。

2 结论

根据上面的模型构建和演化分析，我们得出如下的结论：

（1）(4)式是 Gi(ω，t)演化到稳态时的均衡条件。 从该条件可以看出，采取决策行为ωj的概率不但受到与其他m-1个企业的决策行为相对应的收益的影响，并且表现出递增的态势。

（2）当参数 ξi趋于无穷大时，趋于零。 由于决策行为的的选取是完全随机的不受期望收益的影响，这表明在演化过程中，企业决策行为会受到太大的随机扰动的影响而呈现出随机性特征。

（3）当 ξj趋于零时，从(4)可知，由于受到的干扰较小，采取特定行动的概率中对行动的期望收益的依赖才会不断增加。由于受到随机因素的干扰较小，学习能力才能很快的增强。

（4）在现实的企业决策过程中，决策的扰动既不是ξj趋于无穷大，也不是ξj趋于零，而是具有一定程度噪声的决策行为的学习过程。当整个演化达到稳态时，得出的均衡解是具有某种概率密度的稳态值，是非确定的，它可以看做确定解纳什均衡的扩展值。同时在模型中可以看出降低决策行为的扰动是提高决策能力的有效方法。因此，企业在决策过程中应该通过不断学习，来降低决策行为的的失误和“噪音”的的扰动。

[1]陆瑾.产业组织演化研究[D].复旦大学,2005.

[2]吴彤.自组织方法论研究[M].清华大学出版社,2001.

[3]盛昭瀚,蒋德鹏.演化经济学[M].上海三联书店,2002.

[4]黄登仕,经济系统的密度周期性和复杂性[M].北京大学出版社,2003.

[5]Kwasnicka H,Kwasnieki W，long-term diffusion factors of technological development:an evolutionary model and case study[J].Technologieal Foereasting and Social Change,1996，52.

[6]Potts J,The New Evolutionary Microeconomics:Complexity,Competence,and Adaptive Behavior[M].Cheltenham,Edward Elgar，2000.

[7]Silverberg G,Dosi G,Orsenigo L,Innovation,Diversity and Diffusion:a self-organization Model[J],EconomicJounral,1988，98.

[8]程红莉.学习型企业及其组织学习机制研究[D].华中师范大学,2003.

[9]陈国权,马萌.组织学习过程模型研究[J].管理科学学报,2000,3(3).