产业结构变化对我国能源消费的动态冲击分析

马立平，陈首丽

(1.首都经贸大学 统计学院，北京 100023；2.北京石油化工学院，北京 102600)

0 引言

过去20年中国产业结构发生了很大的变化，1980～1993年，第一产业的比重由31.1%下降到19.9%，第三产业的比重由21.4%上升到32.7%，第二产业的份额在经过较长一段时间的徘徊之后开始呈上升趋势。1995年起，第二产业的发展速度很快，虽然总体上工业化过程中的产业结构变化不利于节能，但其也并不意味着总体GDP能耗必然上升，能源消费不仅取决于产业增加值比重结构及其变化，还取决于产业的单耗变化。为深入分析能源消费总量受产业结构影响的冲击作用，本文采用向量自回归（VAR）模型，以能源消费与各产业产值构成的经济系统为对象，分析产业结构对我国能源消费的动态冲击。

1 模型及分析指标

向量自回归（VAR）模型是一种非结构化的多方程模型，采用多方程联立的模型形式，

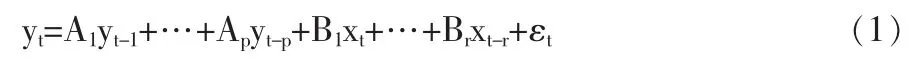
其中，yt是M维内生变量向量，xt是D为外生变量向量，A1,…,Ap和B1,…,Br是待估计的参数矩阵，内生变量和外生变量分别有P和R阶滞后期，εt是随机扰动项。模型中的每一个方程均是内生变量对模型的全部内生变量的滞后项进行回归，从而分析研究对象系统内全部内生变量之间的动态关系。

VAR模型中随机扰动项发生变化时，不仅当前的内生变量会改变，而且其还会通过当前的内生变量影响到其它的内生变量改变，最终又反馈到自身。利用VAR模型进行脉冲响应分析可以用来衡量来自随机扰动项的一个标准差冲击对内生变量当前和未来取值的影响。

我们可以将VAR模型表示成为一个向量移动平均（MA）模型：

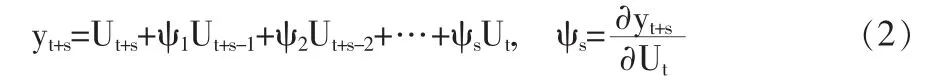
其中，系数矩阵ψs称作脉冲响应函数，ψs中第i行第j列元素看作是滞后s期的函数（s=1,2,3,… ），表示在其它误差项在任何时期都不变的条件下，当第j个变量yjt对应的误差项μjt在t期受到一个单位的冲击 （即一个单位的变化）后，对第i个内生变量yit在t+s期造成的影响，即VAR模型中变量i对由变量j的s期脉冲响应。

在进行脉冲响应分析的同时，VAR模型还可将系统内生变量的估计预测均方误差分解成系统中各变量冲击的结果，即方差分解分析，从而了解各分量对模型每一内生变量的相对重要性，为此定义Rij(s)为第j个分量对第i个分量的方差贡献率：

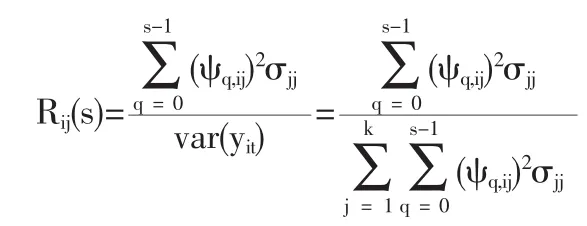
其中ψq,ij是脉冲响应函数，σjj是白噪声序列第j个分量的标准差，yit是自回归向量的第i个分量。如果Rij(s)较大，则意味着第j个分量对第i个分量的影响大，反之则说明影响小。

2 产业结构变化对能源消费总量的冲击分析

2.1 数据来源及说明

（1）本文计算所涉及的变量和数据资料包括第一产业、工业、建筑业及第三产业增加值、能源消费总量，根据数据的可获得性选取 《中国统计年鉴》、《中国能源统计年鉴》中1978～2006年的数据进行分析，其中能源消费总量用EC来表示，各产业增加值分别用G1、GG、GJ、G3来表示。

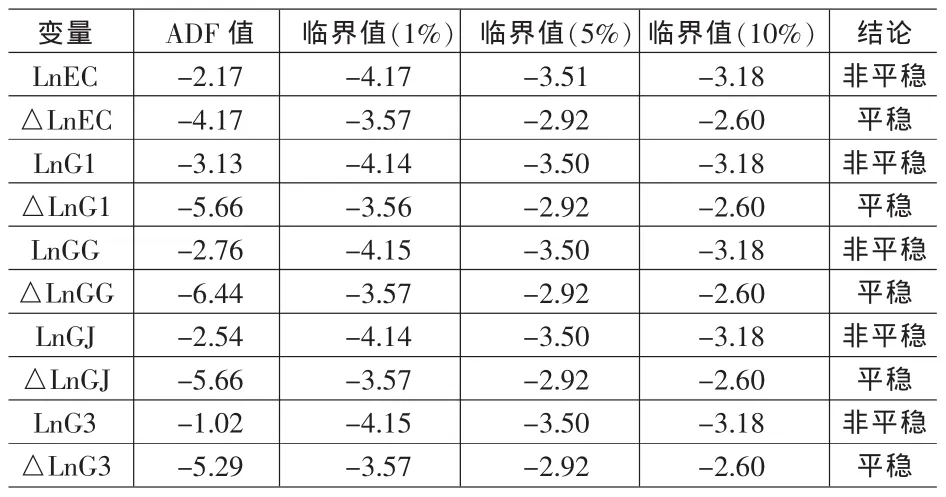
表1 变量平稳性检验结果

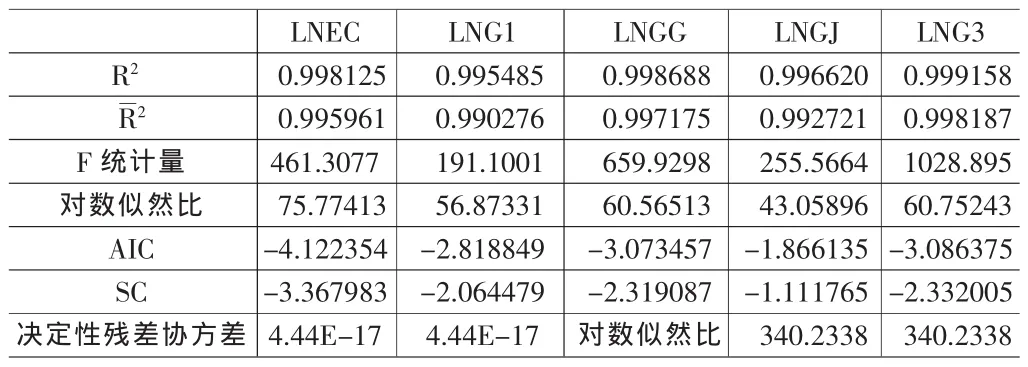
表2 VAR模型回归结果

（2）在进行各项分析之前，考虑到价格因素对时间序列的影响，建立模型前对各产业增加值数据用零售物价指数P进行了调整。

（3）为了避免数据的剧烈波动、时序数列趋势线性化和数据异方差现象对模型估计带来不利的影响，同时考虑到由于数据的自然对数变化不改变函数原来的协整关系，因而本文在分析之前首先对数据进行了自然对数处理，上述变量经对数处理后分别以 LnEC、LnG1、LnGG、LnGJ、LnG3 表示。

2.2 变量平稳性与协整关系检验

采用ADF检验法，根据AIC和SC准则选取滞后阶数，对各变量进行了平稳性检验，检验结果见表1。

表1检验结果表明，所有变量原序列都不是平稳序列，而其一阶差分序列在1%显著性水平下都不拒绝变量有一个单位根的原假设，即这些变量序列均为一阶单整序列，说明各产业增加值与能源消费之间可能存在着长期稳定的协整关系，为确认协整关系的存在，进一步地采用了Johansen极大似然估计法对变量进行协整检验，检验结果显示，在5%水平上至少存在两个协整方程，也就是说变量之间存在长期均衡关系，可以直接建立VAR模型。

2.3 VAR模型的建立

根据AIC和SC最小准则，选择了滞后三期，建立的VAR模型结果表2所示。

从估计结果看，决定性残差协方差仅有4.44E-17，AIC值和SC值也非常小，所以建立VAR（3）模型比较好，可以进行后面的脉冲响应分析以及方差分解分析。

2.4 脉冲响应分析

利用VAR模型计算的脉冲响应函数值，即能源消费总量对各产业增加值一个标准差冲击的响应绘制成图1。

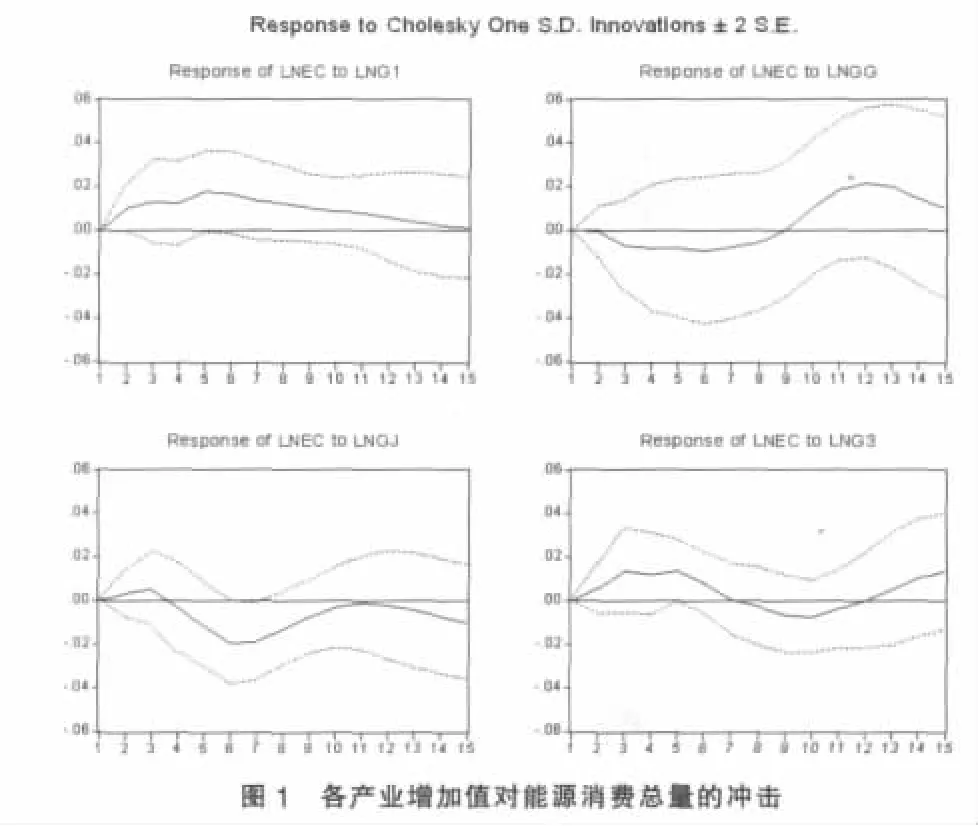
图1中，横轴表示冲击作用的滞后期数，纵轴表示能源消费总量LnEC的数值，实线表示脉冲响应函数曲线，代表了能源消费总量对相应的各产业增加值冲击的反应，虚线表示正负两倍标准差偏离带。从各产业增加值冲击引起能源消费的响应函数曲线来看，各产业对能源消费总量的冲击作用是不相同的，短期与长期的作用效果也有所差别：

（1）能源消费对第一产业冲击的响应比较迅速，在冲击过后的第五年已经达到0.02，此后这种作用有所减小但始终为正向的；而在长期，其影响回复到0附近。这表明短期内，我国农业水平的发展会增加总体能源消耗量，但由于第一产业本身并不过多依赖各类能源，因此从长期来看，农业对能源消费的冲击作用是逐渐减小的。

（2）工业对能源消费的冲击作用主要在于其长期，短期内由于行业结构、产品结构的调整会降低其能源的单耗水平，但其对能源消费总量的作用持续且起到正向的、较大影响。

（3）建筑业对能源消费总量的冲击具有波动性，仅在最初4年呈现正向冲击，此后其负向作用更为突出，这表明可以通过适当扩大建筑业的比重来调节能源的消费总量。

（4）第三产业的冲击作用在起初的七年里都是正向的，即来自第三产业的一个波动将会导致能源消费总量的增加，且这种作用在第三年到第六年达到峰值；进入到影响的第八年后，第三产业的冲击作用为负，即会减少能源消耗；在第12年，第三产业的冲击作用转为正向且略有增大。

从各产业的长期作用进行分析，我们需要在合理控制工业规模的同时，适当调节第三产业与工业间的比例关系，使能源消耗总量得到有效控制。同时，我们仍需特别注意，在调整产业结构的过程中要从长期着手，不可只顾当前的效果。

3 方差分解分析

脉冲响应函数描述的是VAR模型中一个内生变量的冲击给其他内生变量所带来的影响。而方差分解则是从另一个角度描述了系统的动态变化，其主要思想是，把系统中每个变量的波动，即预测均方误差，按其成因进行分解，然后计算出VAR模型中的变量产生影响的每个随机扰动的相对重要性的信息，即变量冲击的贡献占总贡献的比例。

表3是对LnEC的方差分解结果，表中包括7列，第一列是预测期，第二列S.E.中数据为变量LnEC的各期预测标准误差，后七列均是百分数，分别代表LnEC、LnG1、LnGG、LnGJ、LnG3为因变量的方程随机扰动项对各期预测误差的贡献度，每行结果相加是100。

从LnEC方差分解的结果中可以得出如下的结论：

（1）来自LnGG随机扰动项的影响占LnEC预测误差从0.008%上升到10.259%，在除了LnEC本身以外的所有其他变量当中对能源消费总量增长的影响是最大的。

（2）来自LnGl随机扰动项的影响占LnEC预测误差从4.327%上升到17.005%，后减小至8.721%，说明农业的发展对能源消费总量增长也有着重要的影响。

（3）LnGJ随机扰动项的影响占LnEC预测误差从0.458%增加至13.122%，后又降低至6.933%。

（4）LnG3随机扰动项的影响占LnEC预测误差从1.179%快速上升至8.141%，后降低到4.856%又略有上升至5.403%。 说明与 LnGl、LnGG 相比，LnGJ、LnG3的贡献较小，且波动性比较大。

[1]李子奈.高等计量经济学[M].北京：高等教育出版社，2002.

[2]候羽.我国经济发展中的能源消费研究[D].首都经济贸易大学硕士生论文，2009.