体积函数的导函数等于全面积函数的几何体

刘国祥

（赤峰学院 数学学院，内蒙古 赤峰 024000）

体积函数的导函数等于全面积函数的几何体

刘国祥

（赤峰学院 数学学院，内蒙古 赤峰 024000）

应用微分方程的方法，证明了存在圆柱、圆锥、正棱锥，使得其体积函数的导函数等于全面积函数.关键词：圆柱；圆锥；正棱锥；微分方程；齐次方程

1 引言

V'(x)=πx2=S(x).这就是说明半径为x，(x>0)的球的体积函数的导函数等于全面积函数.文[1]证明了存在正三棱锥和正四棱锥，使得其体积函数的导函数等于全面积函数.文[2]证明了存在正n三棱锥，使得其体积函数的导函数等于全面积函数.下面证明存在圆柱、圆锥、正棱锥，使得其体积函数的导函数等于全面积函数.

2 圆柱

定理1 存在圆柱体，使得其体积函数的导函数等于全面积函数.

证明 对于圆柱体，设底面半径为x，(x>0)，高为h(x)，则

体积 V(x)=πx2h(x)

全面积 S(x)=2 πx2+2 πx h(x)

则 V'(x)=2 πx h(x)+πx2h'(x)

设V'(x)=S(x)

就有 2 πx h(x)+πx2h'(x)=2 πx2+2 πx h(x)

因而h'(x)=2

因此h(x)=2 x+c，其中c是使得h(x)>0的常数.

则存在圆柱体，使得其体积函数的导函数等于全面积函数.

3 圆锥

定理2 存在圆锥体，使得其体积函数的导函数等于全面积函数.

证明 对于圆锥体，设底面半径为x，(x>0)，高为h(x)，母线长为l(x).

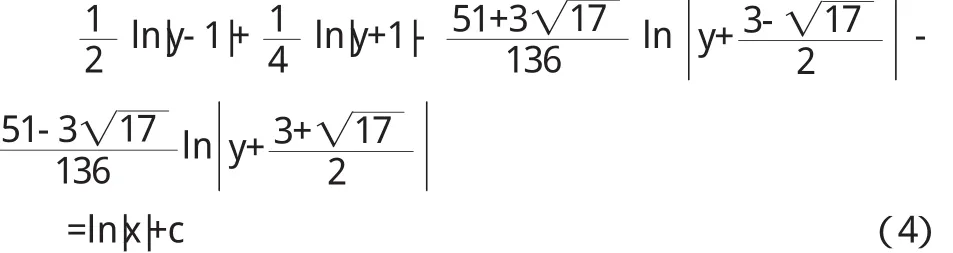
其实，由（1），根据微分方程的有关定理，就说明了解的存在性.当然，以下的证明不难，但是几乎综合了各种积分的计算.

4 棱锥

定理3 存在棱锥体，使得其体积函数的导函数等于全面积函数.

证明 设棱锥的底面边长A B=x,O为底面中心，C是A B的中点.棱锥的高记为O P=h(x)，（图略）把或者（1 0），就得到h(x)关于x的隐函数.其中c2是使得h(x)>0的任意实数.这就证明了定理.

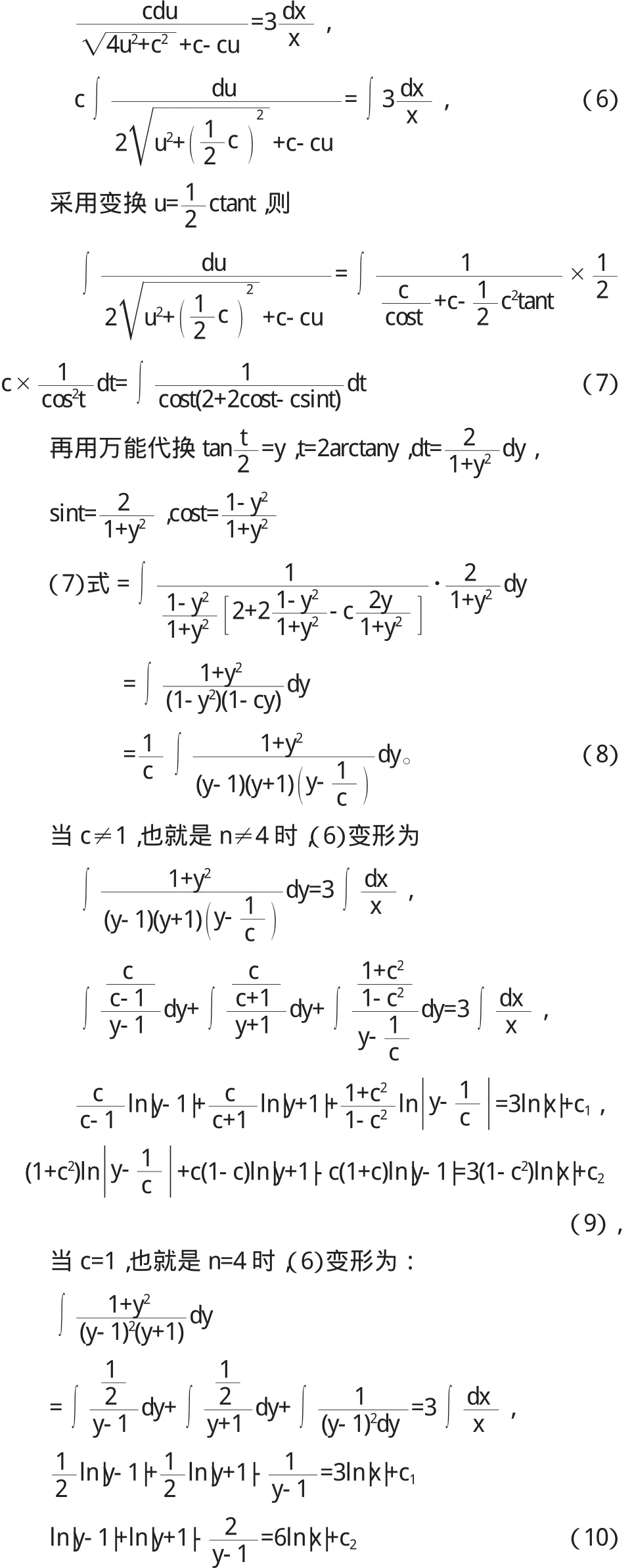
〔1〕张敬坤，李金嵘.一个猜想的解决.数学通讯，2008（19）.

〔2〕薛志成.正n棱柱体积函数的导函数与表面积函数.数学通讯，2009（4）.

O 1 7 4

A

1673-260X（2010）10-0003-02