概率论与数理统计教学方法改革与实践

杨立夫

（陕西理工学院 数学系，陕西，汉中 723000）

概率论与数理统计教学方法改革与实践

杨立夫

（陕西理工学院 数学系，陕西，汉中 723000）

概率论与数理统计是高等学校各专业的一门重要专业基础课.本文结合多年的教学实践，讨论了在教学中如何让学生更好地理解概率统计的概念、方法，同时将数学建模的思想融入到教学过程中，并介绍如何利用Matlab来解决数理统计问题，培养学生利用概率思想分析、解决随机问题的能力.

直观性描述；数理统计；数学建模；Poisson分布

1 前言

概率论与数量统计是研究随机现象统计规律性的一门学科.随机性，特别是随机过程及其数学方法已经广泛而迅速地渗透到计算机科学、生物、医学、工业工程、金融以及自然科学与高新技术等各领域.概率论与数量统计课程已成为理工科各专业一门必修的专业基础课.在多年的教学实践中，深感目前的教学侧重于抽象的理论介绍及繁琐的计算，强调理论的系统性而忽略了概率统计的思想方法及其应用，从而造成了学生在后继专业课程中不会用的尴尬局面.

2 从直观描述到理性思考，使学生更好地理解概率论与数量统计的基本概念和方法

在概率论与数理统计中，许多概念的直观性描述非常容易理解，如频率、独立性、条件概率、均值等，但相应的抽象定义就不那么容易理解了.当学生从直观上感性地理解了这些概念后，如何经过理性思考将它们抽象为严格的数学概念，这个过程不但可以使学生深刻地理解基本概念和基本公式，而且还可以和其它数学类课程一脉相承，在学习过程中逐步培养学生发现问题、分析问题、解决问题的能力以及归纳和类比的能力，为以后灵活地应用概率统计知识理解和解决随机问题打下坚实基础.

例如：（1）从频率→概率的统计定义→概率的公理化定义：由试验观察得到的频率稳定性立即可以得到概率的统计定义，这也为以后数理统计的一些基本思想的理解打下基础，然后通过对频率性质的分析，结合高等数学中极限的相关性质，利用公理化思想抽象就可以得到概率的公理化定义；

（2）从平均值→离散型随机变量的数学期望→连续型随机变量的数学期望：在测量某一工件的长度时，由于随机误差，我们通常取多次测量的平均值作为工件的长度，即x軃=1+2+L m=n，x軃仍为随机变量，而工件的长度是一确定值，如何尽可能地求出其精确值呢？很自然就会想到测量次数越多就会越精确，也即n→∞，此时就趋近于xk出现的概率Pk，从而若用表示其长度就精确了，结合前面概率的定义及事物的复杂性，很自然通过归纳就可得到离散型随机变量X的数学期望.再通过类比，由离散与连续的关系可得，当X为连续性随机变量时，Pk可用f(x)d x代替（其中f(x)为连续性随机变量X的概率密度），此时连续性随机变量X的数学期望可不严格地表示为d x，结合定积分定义立即得到连续型随机变量的数学期望E等等.

通过这些一个个从直观→抽象，从已知→未知的具体过程的展示，一方面可以使学生深刻地理解概念，同时又培养了抽象思维能力和数学素质，为以后灵活地应用概率统计知识分析和解决随机问题以及创新思维打下了坚实基础.

3 注重实践，培养学生的动手能力和创新意识

概率论与数理统计在实际生活和科学研究中有着广泛的应用.注重概率统计的应用，通过解决生产实际中的一些现实问题，不但能激发学生的学习兴趣，还能培养他们自主学习能力和动手能力.这对培养高素质的工程应用型人才是很重要的一个环节.

在教学过程中，我举了一个“摸彩票”模型，在给出了摸彩规则和中奖规则后，让学生回答三个问题：（1）中奖概率与摸彩次序有没有关系？（2）假设发行了2 0 0万张彩票，中一、二等奖的概率各是多少？如果发行1 0 0 0万张彩票中奖的概率又是多少？（3）如果你打算摸彩中奖，在什么条件下中奖概率会大一些？学生很快给出了几种答案，最后和学生一道边分析边讲解，在已知条件下给出了问题解答，让学生明白真正中奖的概率是很小的，要科学看待“摸彩”这一现象.紧接着，又给了两个问题：

(1)保险公司在什么条件下才能盈利？

(2)利用闲暇时间观察2 1路公交车各时段乘车人数，根据观察数据，为该线路设计一个便于操作的公交车调度方案，包括发车时刻表；一共需要多少辆车；这个方案以怎样的程度照顾到了乘客和公交公司双方的利益.

要求学生任选一题统计调查写出书面报告.学生们的兴趣很高，通过查资料、观察完成了作业，取得了较好的效果.通过统计调查，学生可真正深入实际，应用统计方法观察、了解社会，解决一些简单的实际问题.一方面加强并扩展了所学的知识，另一方面培养了学生的动手能力和创新意识.遗憾的是，由于课程内容和学时的限制，这一活动受到很大限制.

4 融数学建模思想于教学之中，提高学生的应用能力

在教学过程中发现很多学生对概念和公式记的很熟，但对一些分布如正态分布、P o i s s o n分布等是如何得到的感到困惑，因此一遇到实际问题就茫然不知所措，不知道该如何应用所学知识来解决.针对这种情况，在教学中将数学建模的思想融入到教学过程之中，通过解决一些实际问题，培养学生的综合应用能力和创新能力.如P o i s s o n分布在保险理赔中的应用.

例1 某保险公司为对该公司的某一保单组合的经营风险做出评估，需要了解该保单组合在一给定的时间区间内的索赔次数的分布.假定所观察的这段时间为(0,t]，将这段时间中到来的索赔次数记为P(t)，请分析索赔发生的统计规律.

解 通过分析，可作如下假设：

（1）在互不相交的各时段内，索赔的发生是相互独立的；

（2）在相同长度的时间段内，索赔发生的统计规律是相同的；

（3）在每一小段时间(t,t+△t)内索赔发生的概率为λ△t+o(△t)

若计Pk(t)为时间段(0,t]内的索赔次数，则有

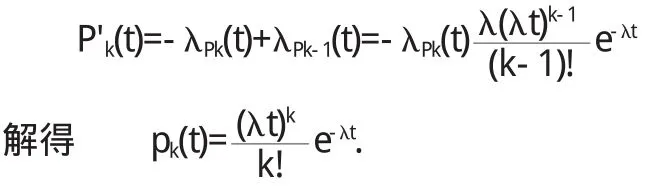
若令t=1就得到在单位时间段(0,t]内的索赔次数为pk(t)即为 P o i s s o n分布.

通过这个问题的解决，一方面让学生了解常见的分布在我们现实生活中生活大量存在的，为日后利用常见分布如正态分布、P o i s s o n分布、指数分布等解决问题树立了一种理念，另一方面，本问题的解决综合应用了微积分、常微分方程、概率统计等知识，对培养学生的综合应用能力也是一种锻炼.

5 Matlab在教学中的应用

随着计算机的广泛使用，将人们从大量繁复的计算中解脱出来，在教学中，通过使用M a t l a b的数据处理功能，将数理统计中大量的数据处理交由计算机处理，学生将主要精力放在理解概率统计的概念、思想和方法上.M a t l a b在教学中的应用主要有两种形式：

（1）模拟试验：如抛掷硬币试验，正态分布模拟试验等；

（2）数据处理：如参数估计、假设检验、方差分析、回归分析等等.

例2（正态分布模拟试验）>>p=r a n d n(3 0 0 0 0,1);

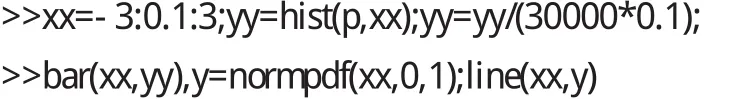
例3（概率计算）已知二维随机变(x,y)的联合概率密度为

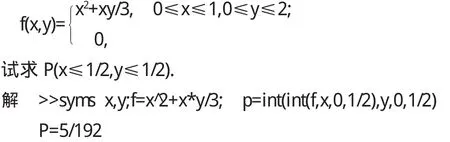
例4[1,4]（假设检验问题）某车间用一台包装机包装葡萄糖，包得的袋装糖重是一个随机变量，它服从正态分布.当机器正常时，其均值为0.5公斤，标准差是0.0 1 5公斤.某日开工后为检验包装机是否正常，随机抽取它所包装的9袋糖，称 得 净 重 为 （ 公 斤）：0.4 9 7，0.5 0 6,0.5 1 8，0.5 2 4，0.4 9 8,0.5 1 1，0.5 2 0，0.5 1 5，0.5 1 2.问机器是否正常工作？

解 用M a t l a b解决如下：

当然，这样做与课程的最后考核方式也紧密相关，必须改变传统单一的考核方式.考核结果有两部分组成：一是闭卷考试，主要考察学生对基本概念、基本思想方法的理解和掌握程度，二是开放性考核，给学生一个实际问题，通过简单的数学建模并借助计算机处理大量数据得到问题的解.

实践证明,通过以概率思想为主线,加强数学建模在教学过程中的渗透,并适当介绍数学软件的应用,可以使原本抽象、枯燥难懂的数学理论变得有滋有味,激发学生的求知欲望,提高学生对该课程的学习兴趣，从而提高课堂教学质量.

〔1〕盛骤,谢式前，潘承毅.概率论与数理统计[M].北京：高等教育出版社,2006：213-215.

〔2〕刘海峰,等.从数学建模角度思考《概率论与数理统计》的教改途径[J].科技创新导报,2009(6):140.

〔3〕萧树铁.随机数学[M].北京：高等教育出版社,2000：86-87.

〔4〕张德丰.Matlab概率论与数理统计分析[M].北京：机械工业出版社,2010:161-166.

G 6 4 2

A

1673-260X（2010）10-0206-02