哲学美的升华——谈解析几何中的哲学观点

陈华喜

（蚌埠学院 数理系，安徽 蚌埠 2 3 3 0 3 0）

哲学美的升华
——谈解析几何中的哲学观点

陈华喜

（蚌埠学院 数理系，安徽 蚌埠 2 3 3 0 3 0）

解析几何与哲学有着许多的内在联系，解析几何定律中蕴含着哲学，同时哲学又指导着解析几何的发展.把哲学思想寓于解析几何教学之中，运用哲学原理指导解析几何学习，能够使学生更好地掌握解析几何知识，增强学生的辩证思维，提高学习效率，取得好的教学效果.

解析几何；哲学；观点

哲学是研究自然界、人类社会和思维发展一般规律的科学，是一种理论化、系统化的世界观；而数学是研究现实世界空间形式和数量关系的具体科学.哲学为数学提供方法论指导，是数学教师指导工作和生活的重要工具，同时又是数学教学的重要目的之一.数学遵循哲学规律而产生、变化、发展,解析几何作为数学的分支，是一门变量学科，其中也蕴涵着丰富的哲学思想.恩格斯说：“有了变数，辩证法进入了数学”.因此，在解析几何教学中进行哲学思想的渗透有十分重大的意义.

1 解析几何中的唯物论观点

1.1 普遍联系的观点

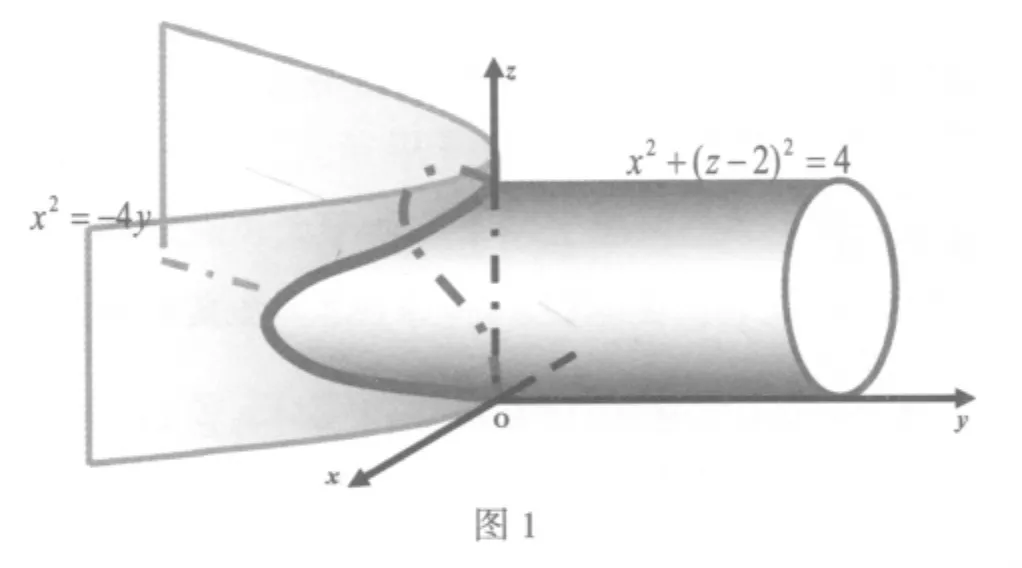
普遍联系是物质世界存在的真实形态.联系作为唯物辩证法的基本范畴，是指世界上一切事物都处在普遍联系之中，事物之间以及事物内部的各要素之间相互依赖，相互影响，相互制约，相互作用.解析几何中的内容也不是孤立存在的，它们之间存在着千丝万缕的联系.在解析几何中，向量以及向量的数量积和向量积的表示方法就有代数表示和几何表示，这两种表示方法之间存在着内在的联系；另外，直线和平面方程的各种表示形式以及点线面的相互关系的判定条件都有几何和代数两种形式，这都体现了联系的观点.再如，点的运动可以产生曲线，曲线与曲线的相交可得点，曲线的运动可以产生曲面，曲面与曲面相交可得曲线，我们也往往利用这一普遍联系方法来获得空间曲线，如空间曲线可以看作射影柱面x2+(z-2)2=4与x2=-4 y的交线（如图1）.

1.2 运动、变化、发展的观点

事物是不断变化、发展的，在事物发展过程中，内部矛盾是事物发展的根本动力，外部矛盾是事物发展的外在动力.数学也是不断发展的，在数学发展过程中，内部矛盾和外部矛盾共同起作用.例如，在解析几何中，椭球面=1可以看作是旋转椭球面经过坐标的拉伸变换而得，并且可以看成是由一个椭圆的变化（大小位置都改变）而产生的，这个椭圆在变化中保持所在平面与x o y平面平行，且两轴的端点分别在两个椭圆上滑动。另外，双曲面、椭圆抛物面也可由相应的旋转曲面经过坐标的拉伸变换得到，并且也可由相应曲线的运动、变化而得到.这种运动、变化、发展正突现了解析几何的本质所在.

2 解析几何中的辩证法观点

2.1 对立统一观点

对立统一规律是唯物辩证法的实质和核心，它揭示了事物发展的源泉和动力在于事物内部的矛盾性，矛盾对立面的统一和斗争推动事物的发展.每一种数学理论中都含有互相矛盾的双方，它们既对立又统一，构成这种理论存在和发展的前提.解析几何中到处充满着矛盾，充满着各种对立面的转化.例如，直线可以看成半径为无穷大的圆，半径为无穷大的圆也可以看成直线.就是说在这种意义下，直线和圆可以互相转化.又如，平面可以看成半径为无穷大的球，半径为无穷大的球也可以看成平面，在这种意义下，两者是统一的，可以互相转化、替代.再如，解析几何中的“数”与“形”是一对矛盾，它们的对立体现在“数量”与“图形”是两个不同的概念.它们的联系是，每个图形及其几何特征有着相应的函数表达式，每个函数及其某些特征有着相应的几何意义.正是“数”与“形”的对立统一构成了解析几何这门学科存在的基础.

2.2 主要矛盾与次要矛盾在解析几何教学中的应用

唯物辩证法认为，在复杂事物之中，存在着许多矛盾，主要矛盾在事物发展过程中处于支配地位，起决定作用.主要矛盾和次要矛盾相互联系、相互影响.

解析几何中，在学习直线和平面的相关位置时，只要注意到直线的方向向量和平面的法向量这一主要矛盾，便可以轻松地解决直线与直线、直线与平面、平面与平面位置关系判定条件以及两异面直线公垂线方程、点到直线或平面的距离等问题.如直线l:和平面π:A x+B y+C z+D=0，判定其位置关系只要根据直线l的方向向量v軆={X,Y,Z}和平面 π 的法向量n軋={A,B,C}的位置关系来判定即可：①相交的充要条件：A X+B Y+C Z≠0，②平行的充要条件：A X+B Y+C Z=0,A x0+B y0+C z0+D=0，③直线在平面上的充要条件：A X+B Y+C Z=0,A x0+B y0+C z0+D≠0.当然，在学习解析几何其它内容时，我们也应当注意处理好主要矛盾与次要矛盾这一关系，这样不仅有助于我们理解、学习，更有助于加深我们的记忆.

2.3 量变、质变的观点

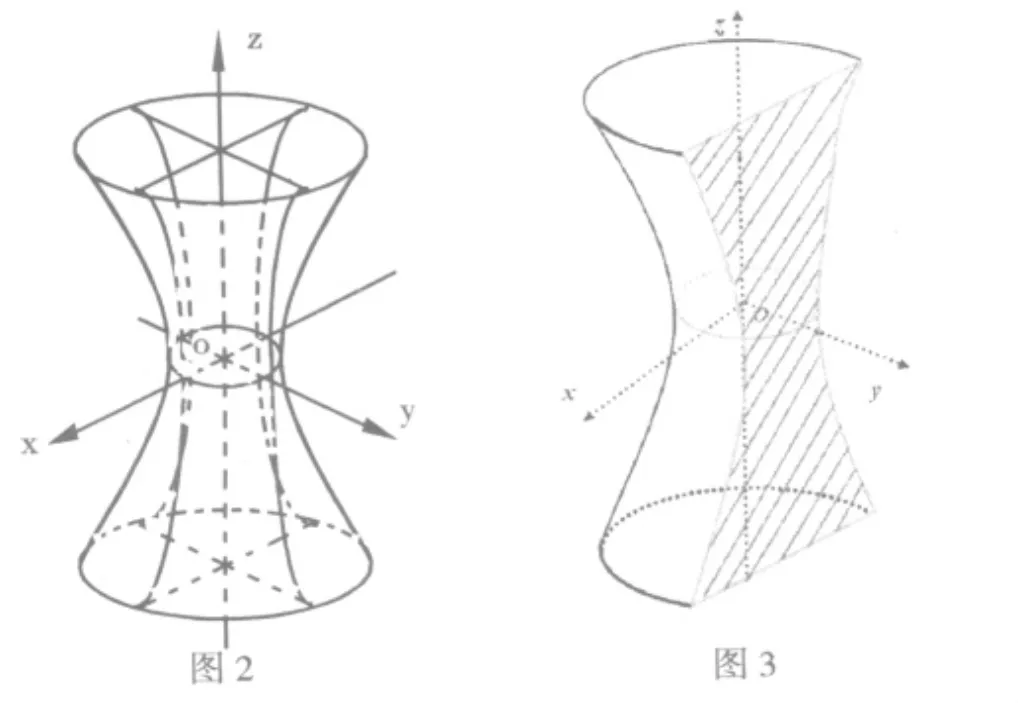
事物的发展变化都表现为由量变到质变，再由质变引起新的量变的反复过程.数学理论的变化和发展符合量变质变规律.数学中每种概念的存在都有着特定的量的界限，如果量变超出了这个界限，就会发生质变，形成另一种概念，这种新概念又存在着自己特有的新的量变.在解析几何中，从二维向量到三维向量，甚至更多维向量，由于维数的增加，这个量变引起了质变，使平面图形变成了空间图形，甚至更为抽象的“体”.比如，方程x+y=1在二维平面上表示直线，而在三维向量空间中则表示平面；而方程x2+y2=1在二维向量空间（平面）上表示中心在坐标原点，半径为1的圆，而在三维向量空间中则表示中心在z轴上，半径为1的圆柱.又如，在空间直角坐标系下，方程表示单叶双曲面（图2），用平面y=h截曲面，得，当|h|

图4

图5

3 解析几何中的认识论观点

3.1 实践的观点

实践是人们能动地探索和改造现实世界的一切活动，实践是认识的基础，也是认识发展的动力.解析几何知识的形成过程有着丰富的物质背景，这些物质背景都反映了人的认识来源于实践，是客观现象作用于人的大脑的结果.它与实践的依赖关系体现在运用解析几何知识解决生产实践中的实际问题.比如，运用旋转曲面的知识，可以制做生活中的很多种使用物品，如现实生活中的救生圈、花瓶、卫星接收器等等；又如，根据单叶双曲面的直纹性可知发电厂冷却塔等建筑物的构建原理；再如，使两个抛物线互相垂直且开口方向相反，让一条抛物线不动，另一条抛物线在其上滑动，就可以得到马鞍面，根据这个理论，人们就可以做出马鞍模型.这种理论与实践的结合，有利于我们深刻、广泛地从实际事物的量的关系和空间形式来正确地认识世界和能动地改造世界.当然用数学得出的结果是否正确要经过实践的检验，实践是检验真理的唯一标准.

3.2 相对性与绝对性

事物是相对的，又是绝对的，解析几何中的许多研究对象也是如此.例如，前面谈到的方程x+y=1在平面上表示直线，在空间则表示平面；而方程x2+y2=1在平面上表示圆，在空间却表示圆柱.又如，方程f(x,y,z)=0在空间表示点的集合（绝对的），一旦x,y,z满足特定关系，将表示一具体几何图形（相对的），比如方程表示马鞍面，等等.在学习过程中，如果认识不到相对性和绝对性，就容易产生思想上的混乱.

总之，解析几何内部处处蕴含着哲学思想，这就要求教师应具备足够的哲学知识，并能用哲学的观点去分析几何的发展、从事几何教学，这才能变抽象枯燥为具体生动，才能将教学内容安排得精细周密使自己的语言丰富而充满哲理，达到理想的教学效果.

〔1〕吕林根.许子道.解析几何(第四版)[M].北京:高等教学出版社,2006.

〔2〕戴美凤.数学思想方法在解析几何教学中的应用[J].宁波大学学报,2001（3）.

〔3〕叶敦平.马克思主义原理[M].北京:高等教育出版社,1999.

O 1 8 2.2

A

1673-260X（2010）10-0005-02