数字摄影测量在桁架结构承载变形监测中的应用研究

牛 鹏

（延安大学 西安创新学院，陕西 西安 7 1 0 1 0 0）

数字摄影测量在桁架结构承载变形监测中的应用研究

牛 鹏

（延安大学 西安创新学院，陕西 西安 7 1 0 1 0 0）

在建筑行业中大量使用桁架结构，然而由于其结构复杂，理论分析和数值模拟均无法准确估计其承载受力变形情况，为此，本文提出一种基于数字摄影测量的桁架结构变形监测方法.该方法通过跟踪粘贴在桁架表面的人工标志点，计算关键监测点在不同时刻的位移信息，来了解桁架在承载过程中的整体变形情况，从而为桁架力学性能分析提供定量参考.对该方法涉及的关键技术如标志点识别，三维重建，变形点跟踪等进行了详细的研究.为了提高摄影测量解算的精度及效率，提出了基于最小二乘法的捆绑调整算法.实验结果表明，该方法精度基本可以满足桁架结构变形监测的精度需求，为桁架变形监测提供一条可行的途径.

桁架结构；变形监测；数字摄影测量

桁架结构广泛应用于建筑行业，因而对其安全性能的评估至关重要.桁架结构的安全性主要取决于其力学性能.然而，由于试验分析过程中，桁架结构实验尺寸大、变形大、应力分布十分复杂的特点，传统的位移传感器和电阻应变片等无法满足大变形测量的需要[1].随着弹塑性单元和非线性数值解法的发展,以及近年来计算机硬件水平的飞速提高,有限元分析模型逐渐成为主流.然而，由于桁架结构的受力状态十分复杂，对其进行精确的理论分析尚有很大的难度.

本文提出了一种非接触式三维光学桁架结构变形观测的新方法.该方法采用数字摄影测量技术，通过跟踪粘贴在桁架结构表面的众多人工标志点，计算标志点三维坐标在不同时刻的位移信息，来分析桁架结构的整体变形情况.为了验证该方法的有效性，分别进行了精度验证实验以及桁架结构变形观测实验，并将测量结果与全站仪进行了对比分析.

1 测量原理

物方点经过相机镜头摄影后成像到像平面上，理想的投影成像模型是几何光学中的小孔成像模型，其本质就是射影几何中的中心透视投影过程.相机实际成像时，由于各种因素的干扰，主点的像平面坐标不严格为零，存在一微小值(x 0，y 0)，使得像点在像平面上相对其理论位置存在一定的微小偏差，记为(Δx′，Δy′).实际像点的共线方程可以写成[2]：

对同一个物方点P来说，在内外方位参数已知的情况下，只要知道P点在2个以上图像上的二维坐标（x,y），根据公式1列出3个以上的方程构成方程组，就可求解出其在空间中的三维坐标（X，Y，Z）.

2 桁架结构变形测量过程

桁架结构变形测量的流程如图1所示，首先在关键监测点粘贴人工标志点，围绕桁架结构拍摄照片，保证每个人工标志点至少在5张照片上出现；其次，识别照片中的人工标志点，并根据公式（1）重建人工标志点的三维坐标，用捆绑调整算法进行平差；最后将各个时刻重建的关键监测点的三维坐标通过三点坐标对齐法将坐标系归一，从而计算桁架结构在受力过程中各个时刻的变形量.

2.1 标志点识别及三维重建

标志点包括编码标志点及非编码标志点两种类型.非编码标志点通常采用黑白相间的颜色，主要考虑标志点自身颜色和背景颜色有尽量大的反差编码标志点具有唯一的编号，这样就可以对这些标志点实现自动的检测与识别.为了简化图像处理难度和提高测量的自动化程度，本文采用圆形非编码标志点及环形人工编码标志点，如图2所示.

图2 人工标志点

圆形标志点经过透视成像后成为椭圆，为了对椭圆进行识别和中心定位，就需要进行图像处理，一般处理步骤包括：边缘检测、亚像素边缘提取与椭圆中心拟合[3].首先使用C a n n y算子进行边缘检测[4]；在结果中搜索可能的椭圆边界，同时排除不可能的边缘；对确认为椭圆边界的图像点使用梯度均值法进行亚像素修正，然后使用最小二乘法拟合得到椭圆中心和长短轴、旋转角等信息.

人工标志点识别完成后，即可根据共面方程[3]确定两幅图像之间的位置关系.并以此确定世界坐标系，一般情况下将第一幅图像的坐标系作为世界坐标系.然后依据共线方程[2]确定任意一幅图像相对于世界坐标系的绝对方位.由于编码点在每张照片上都显示其唯一的I D,通过I D可以对其进行匹配.对于非编码点基于核线约束条件进行匹配[3].由于核线约束是一维约束，而且像点存在误差，所以仅考虑两幅图片时，很容易产生歧义性，利用多幅图片之间相互进行极线匹配就可以大大降低匹配的出错率.匹配成功后依据公式（1）列方程即可求解每一个人工标志点的三维坐标.

2.2 基于最小二乘法及自由网平差的捆绑调整算法

将像点坐标记为L,L=(l1,l2,……ln)T，未知量（物体点坐标、相机参数）记为X,X=(X1,X2,…Xu)T.依据共线方程知：真实像点坐标L軌与真实未知量X軒之间的关系可以用函数φ表达为：

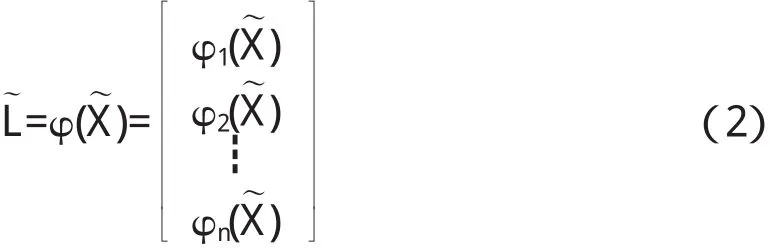
由于像点坐标及未知量的真实值均不可知，于是真实像点坐标L軌可以用观察值L与一个偏差v之和来表示，未知量真实值X軒用估计值X赞代表，于是，公式（2）可以展开为：

假设未知量的初值为 X0，那么X赞=X0+x赞.如果x赞足够小，那么公式（3）可以用泰勒公式展开为：

2.3 坐标对齐及变形量计算

各个时刻重建的监测点三维坐标处于自由坐标系中，为了进行变形量计算，需要将各个时刻的坐标进行归一，本文采用三点法进行坐标系的归一化.坐标归一化以后，即可依据公式（6）计算出各个时刻的三维变形量.

其中，(ΔX,ΔY,ΔZ)为变形向量，(Xi,Yi,Zi)为某一监测点在第i时刻的三维坐标，(X1,Y1,Z1)为该监测点在变形前的三维坐标.

3 试验结果及分析

3.1 精度分析

以某实际桁架为实验对象，如图3所示，在关键部位粘贴人工标志点，然后用本文方法进行变形监测.首先设置6个关键观测点1-6，及三组距离：1-2、3-4、5-6.在静止状态下重复测量6次，实验结果如表1所示.依据3S i g m a准则知，本文方法的精度可以达到0.8 m m/m.由此可知本文方法完全满足桁架测量的精度需求.

图3

表1 三组距离值重复测量6次

3.2 桁架变形测量

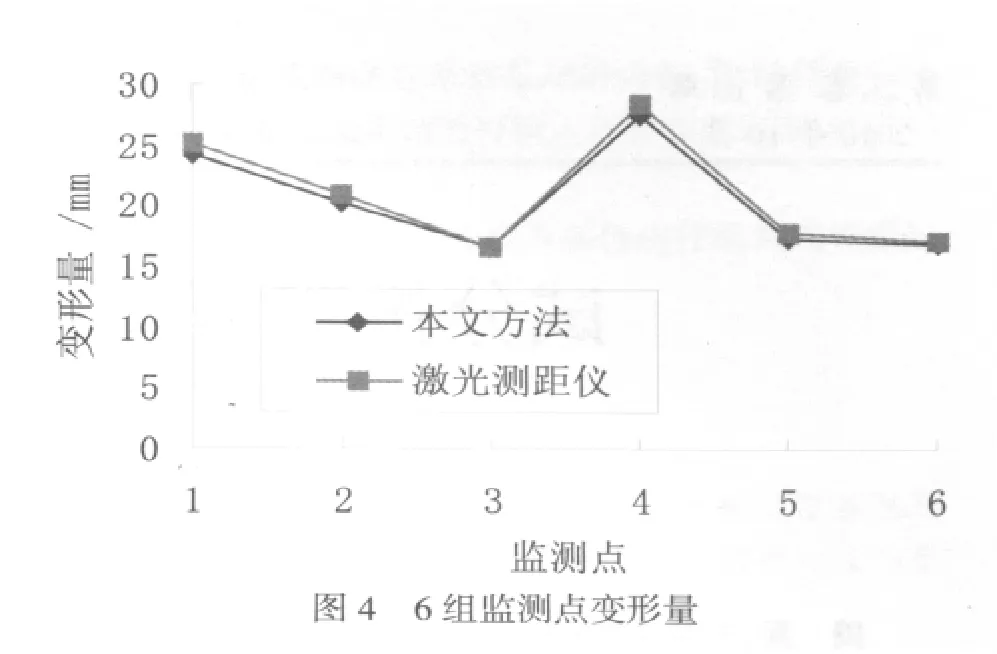
为了监测桁架结构变形量，对桁架结构施加载荷，当变形趋于稳定时，围绕桁架结构进行拍摄照片，重建出三维坐标后，依据固定不动的参考点进行坐标对齐，最后计算变形量.当施加一次载荷后，6个观测点的变形量如图4所示.监测的结果同时与激光测距仪测量的结果进行对比，其中全站仪的精度为1.0 m m+1.0 p p m.由图可以看出本文方法与激光测量方法测得的变形趋势较一致.从而进一步验证本文方法的有效性.

4 结论

桁架结构的力学性能决定桁架结构的安全性，为了精确地获取桁架结构的力学性能，本文提出了基于数字摄影测量的桁架结构变形监测方法.详细讨论了标志点识别及三维重建等关键技术.为了提高系统精度，提出了基于最小二乘法的捆绑调整算法.最后将本文方法应用于某实际桁架承载变形测量过程，实际结果表明，本文方法可以满足桁架结构变形监测的精度需求.除此之外，本文方法还具有非接触、测点多的优点.

〔1〕于承新,全景,李福柱，等.近景摄影观测钢结构挠度变形的实验研究[J].山东建筑工程学院学报,2000,26(2):31-42.

〔2〕冯文灏.近景摄影测量[M].武汉大学出版社,2002.125-130.

〔3〕邾继贵,叶声华.基于近景数字摄影的坐标精密测量关键技术研究[J].计量学报,2005,26(3):207-211.

〔4〕J.Canny.A computationalapproach to edge detection.IEEE Transactions on Pattern Analysis and machine Intelligence.PAMI-8(Vol.6):679-698(1986).

T U 3 7 5.5

A

1673-260X（2010）10-0105-03