高速双体船斜浪中运动响应及连接桥波浪载荷预报

耿彦超，顾学康，汪雪良

（中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

高速双体船作为一种新型高性能船舶，与单体船相比，它具有甲板面积大，操纵性和稳定性好等优点，它不仅可以作为货船、客船和渡轮，而且可以用于海洋开发和海洋钻探等。目前高速双体船应用范围越来越广，越来越受到各国军方、执法和旅游等部门的关注，但是国际上对高速双体船总体和结构性能的研究还很不充分，各国船级社在结构设计计算方面的规定也很不一致，导致现阶段的高速双体船设计水平和需求不相适应，双体船在海上运营的安全性无法得到保障。为寻求更为可靠的结构设计方法，船级社等船舶科研机构已把注意力集中到高速双体船的运动响应、波浪载荷预报和结构响应等研究方面，以适应未来航运市场对高性能双体船的需求。

目前船舶运动和载荷的传统预报方法是基于细长体假设的切片法，切片法具有计算快捷、对船型适用性好等诸多优点因而在船舶工程界得到了普遍的应用。但由于切片理论是基于高频低速假定的，在计算流场解时，分别求解船舶诸横剖面柱体振荡流场，不能考虑切片间的流体干扰作用，高航速下切片法对船舶运动响应的预报理论结果与试验结果比较出入较大，这就限制了切片法在高速双体船运动和载荷预报上的进一步应用。准确预报高速双体船的运动及载荷响应对双体船设计单位和设计者非常重要，近几年发展起来的二维半理论用比切片理论更为准确的方法来处理有航速问题，二维半理论即高速细长体理论最早由Chapman（1975）[1]提出，而后由很多学者将其扩展到船舶耐波性及载荷领域等的预报，二维半理论保留了其定解问题在自由面条件中流体动力计算最为重要的航速效应，且定解问题满足二维控制方程，仅需在各个船体横剖面上求解拉普拉斯方程，计算效率大大高于三维有航速方法，这些优点使其特别适合于高速双体船运动和载荷响应预报。但是目前，国内外学者对二维半理论的研究工作主要集中于单体或多体船舶的运动特性，对高速船舶的波浪载荷尤其是双体船舶连接桥结构在斜浪中承受的波浪载荷研究较少。尽管一些学者开展了高速船舶的运动和波浪载荷的水池模型试验，但理论预报计算结果与模型试验的比较也很不充分。

本文通过二维时域格林函数法求解三维频域速度势定解条件，建立了双体船在规则波中的运动及连接桥结构载荷响应方程；然后应用二维半理论和程序进行计算，并把计算结果同模型试验结果、二维双体船计算程序和SESAM等程序计算结果进行比较分析，初步验证了二维半理论和程序在预报高速双体船运动及波浪载荷性能中的适用性。

2 二维半理论及其数值求解

2.1 坐标系的建立

为了描述波浪和双体船运动，需要引入三个右手坐标系如图1所示及下面表述[2-3]：

（1）空间固定坐标系O-XYZ：原点O位于未扰动的静水面上，OX轴与入射波浪传播方向相反，OZ轴竖直向上，用这个空间固定坐标系来表示入射波最为方便。

（2）随船平动坐标系o-xyz：原点o位于未扰动的静水面上，ox轴与船舶航行方向一致，oz轴竖直向上，通过船舶的重心，oxy平面与静水面重合。

（3）固连船体坐标系G-xbybzb：原点G为船舶重心，Gxb轴平行于船体基线指向船艏，Gzb轴垂直于船体水线面，用这一坐标系表述船体表面。

设船舶在规则波中以恒速U沿x方向前进，t=0时刻点o与O重合，入射波浪沿-X方向传播，浪向角为β（顶浪时β＝180°）。当船舶无摇荡运动时，点o与G位于同一铅垂线上。船舶重心至水线面的距离为oG，以G点位于水线面上方时为正。则坐标转换关系为：

2.2 定解条件的建立、求解和非定常扰动流场的水动力计算

当根据上述坐标系系统建立速度势定解条件后，求解该定解问题一般需采用三维有航速频域格林函数的面元法，但是此法计算费时，而计入航速效应的二维半理论更适合于高速船舶在波浪中运动的水动力问题，应用二维半理论计算时首先采用细长体理论假定，不计定常扰动势的影响，然后将三维Laplace方程简化为各切片平面上的二维Laplace方程，最后可以计算非定常流场的水动力性能，包括辐射水动力计算、绕射水动力计算、Froude-Kriloff力计算和静水恢复力计算等[4]，详细推导过程及说明见文献[5]。

3 高速双体船规则波中稳态运动响应

3.1 运动微分方程的建立和求解

依据达朗贝尔原理，建立船舶在规则波中的五自由度（缺纵荡）运动微分方程（以重心G为矩心）有如下的形式，详细推导过程见文献[3]与文献[4]：

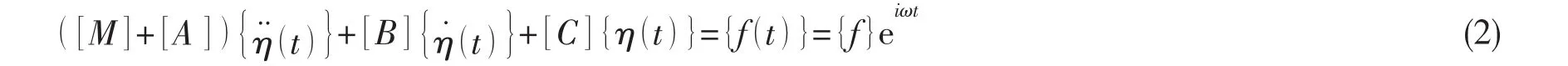
式中，［M］为船舶的质量矩阵，｛f｝=｛fC｝+i｛ fS｝为波浪干扰力的复数振幅。

设 ｛η（t）｝=｛η ｝ eiωt，｛η ｝=｛ηC｝+i｛ ηS｝为运动位移的复振幅。

解此方程组，可得到船舶运动的稳态解

3.2 WP60双体船算例分析

WP60双体船总长60.0m，型宽18m，吃水1.96m，由两个具有穿浪艏部线型的片体、连接桥和艏部中间体构成，在中国船舶科学研究中心耐波性水池中进行过在规则波和不规则波中的运动和波浪载荷模型试验，试验中采用的航速26Kn，相当于Froude数0.592。

以下对该高速双体船利用基于二维半理论编写的计算机程序进行顶浪（180°）和艏斜浪（135°）航向下的运动预报结果（以“2.5d”表示）和模型试验（以“experiment”表示）、SESAM[6]程序预报（“以“sesam”表示”）和二维双体船理论[7]预报（“以“2d”表示”）结果进行比较分析，以验证本文方法对高速双体船运动响应预报的适用性。

图2-7为顶浪（180°）情况下WP60穿浪双体船垂向运动计算结果与模型试验传递函数的比较，加速度计算点的位置与模型试验测点一一对应。可以看出，与模型试验值相比，在传递函数峰点附近本文方法和SESAM计算都给出了偏大的响应预报值，显然，在峰点附近，流体的粘性阻尼不可忽略；而二维双体船理论预报值（2d）预报结果较好，但是其预报的垂荡和纵摇运动响应曲线逐渐出现两个或两个以上的峰值，这可能就是由双体船片体之间的自由液面所导致的“伪共振”现象[7]；在其它位置，本文方法给出了较好的预报结果。对于纵摇运动，随着波长的增加，理论预报计算结果与模型试验结果的变化趋势基本一致，但量值上有一定的差别。对于垂向运动加速度，本文方法预报结果与模型试验结果在变化趋势和量值上都比较一致，艉部预报结果略大。

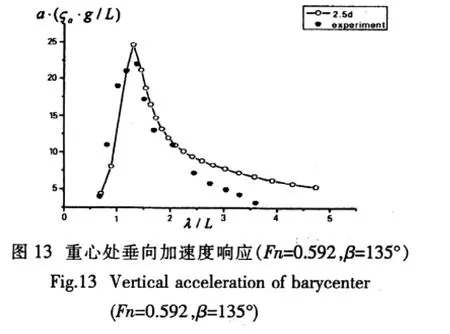
图8-14为艏斜浪（135°）状态下，WP60穿浪双体船垂荡、纵摇、横摇和垂向加速度运动计算结果与模型试验传递函数的比较。可以看出，与模型试验结果相比，在波长较短时，垂荡和纵摇运动理论计算结果之间差别不大，与模型试验结果也比较接近；在传递函数峰点附近，理论计算结果一般偏大；随着波长的进一步增加，理论计算结果之间的差别变得明显，本文方法与模型试验结果相比，垂荡偏大纵摇偏小。对于横摇运动，通过不断调整粘性阻尼，SESAM可以预报出和模型试验值十分一致的结果，而本文计算值偏小。对于垂向加速度响应，本文方法计算的加速度与模型试验结果基本一致。

4 高速双体船连接桥结构规则波中波浪载荷数值计算

4.1 双体船连接桥结构

随着双体船的大型化，结构重量控制和连接桥结构的变形、强度、稳定性和疲劳设计之间的矛盾日益突出。双体船由于片体间连接桥结构的存在，在船体结构设计中除了需要进行与单体船类似的横剖面纵向构件的强度校核外，还需特别关注连接桥结构的横向强度问题。连接桥结构横向构件相对比较薄弱，并且由于与片体的连接部分存在几何和结构的突变，容易引起应力集中。因此，连接桥结构的强度、刚度、稳定性和疲劳问题是双体船船体结构设计的关键技术，而该结构在波浪中受到的波浪载荷的预报和设计载荷的确定是保证船体结构设计成功的前提条件。在双体船在波浪中运动二维半理论和数值求解的基础上，根据刚体动力学平衡原理，可求解双体船横剖面和连接桥纵向剖面上的波浪诱导载荷[3]，本文只给出连接桥纵向剖面的波浪诱导载荷。

4.2 WP60双体船连接桥波浪载荷计算

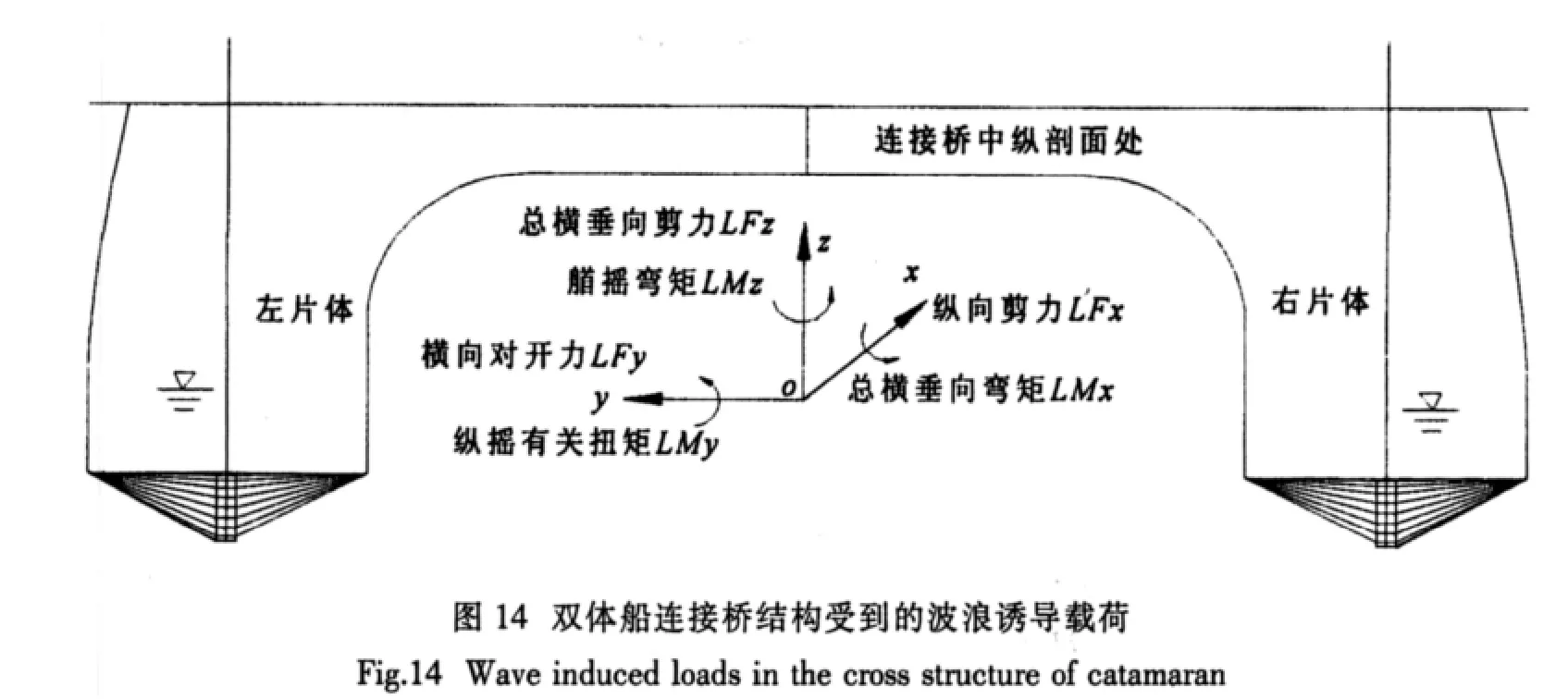
利用双体船船型、结构和重量分布的左右对称性，将双体船沿中纵剖面切开，研究连接桥结构纵向剖面上的波浪诱导载荷，如图14所示，约定纵向剖面载荷的指向与坐标轴同向时为正，由文献[8]可知连接桥中纵剖面的载荷包括：总横垂向弯矩（由两片体相对横摇引起）LMX、纵摇有关扭矩（片体不同步纵摇引起）LMY、艏摇弯矩（由两个片体不同步艏摇引起）LMZ、横向对开力（由两个片体不同步横荡引起）LFY、总横垂向剪力（由两片体不同步垂荡引起）LFZ和纵向剪力（由两个片体不同步纵荡引起）LFX。

根据片体受到的惯性力和流体力相平衡，应用达朗贝尔原理，可以得到连接桥中纵剖面波浪诱导载荷各分量(缺少纵向剪切力)，详细推导过程见文献[5]：

其中：FI2…FI6为片体受到的入射波干扰力（矩），FR2…FR6为片体受到的辐射波浪力（矩），FD2…FD6为片体受到的绕射波浪力（矩），Fsz，Mso，Msy为片体受到的静水恢复力（矩），Fiy，Fiz，Mix，Miy，Miz为片体受到的惯性力（矩）。

以下给出了WP60高速穿浪双体船在不同航速下连接桥结构上的波浪载荷传递函数及与模型试验结果的对比。图中的横坐标为波长船长比（λ/）L ，纵坐标为无因次化的连接桥波浪载荷，包括双体船连接桥中纵剖面上的总横垂向弯矩LMX、纵摇有关扭矩LMY、艏摇弯矩LMZ、横向对开力LFY和总横垂向剪力LFZ。同样，垂向和横向剪力用因子ρgBLppζa进行无因次化，力矩用因子ρgBL2ppζa进行无因次化。

实船航速 26Kn，33Kn 和 40Kn（Fn=0.592、Fn=0.75 和 Fn=0.9），航向 150°（艏斜浪）情况下，WP60穿浪双体船连接桥结构波浪载荷的传递函数如图14-19。由图中可以看到，双体船连接桥载荷在Fn=0.75时相对较大。对双体船来说，航速效应和片体间的水动力干扰对连接桥结构的波浪载荷均会产生影响。

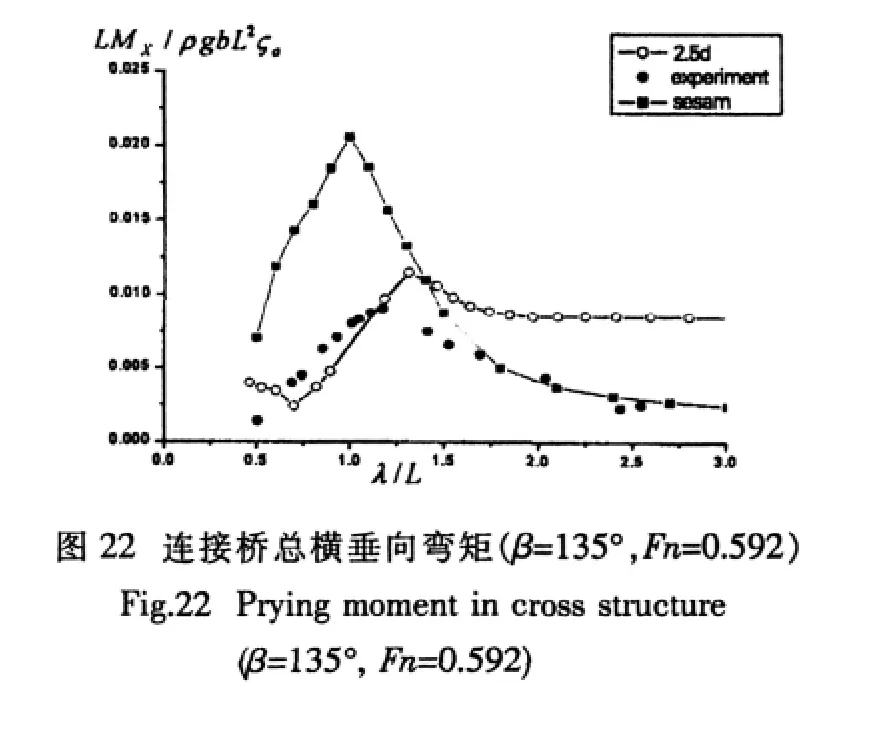
图20-22为航速26Kn，航向135°（艏斜浪）时WP60双体船理论预报值与模型试验值的对比。从图20可以看出连接桥横向对开力理论预报值与模型试验值较符合；从图21可以看出本文二维半理论预报连接桥总横垂向剪力结果小于模型试验值；从图22可看出二维半理论程序与SESAM都给出了偏大的预报结果，但二维半理论计算结果较SESAM计算结果更接近试验值。

5 结 论

通过理论计算与模型试验的对比分析，本文主要得出以下结论：

（1）二维半理论可较为准确地预报高速双体船在顶浪和斜浪中的运动响应。同时对比模型试验结果发现，本文发展的二维半理论程序在峰值处给出了偏大的预报结果，表明了流体的粘性阻尼对准确预报运动响应的重要性。

（2）由于二维半理论相对二维切片理论计及了自由面的航速效应，所以在计算时消除了由于双体船片体之间的自由液面所导致的“伪共振”现象。

（3）双体船舶连接桥横向构件结构相对比较薄弱，需特别关注连接桥结构的横向强度问题。应用本文发展的二维半理论程序可初步预报双体船连接桥结构波浪载荷，但仍需开展进一步的研究工作。

[1]Chapman R B.Numerical solution for hydrodynamic forces on a surce-piercing plate oscillating in yaw and sway[C]//Proc.lst Int.Conf.Numer.Ship Hydrodyn.David W.Talor Ship R&D Cente,Betheda,Maryland,1975:333-350.

[2]刘应中,缪国平.船舶在波浪上的运动理论[M].上海:上海交通大学出版社,1986.

[3]戴仰山,沈进威,宋竞正.船舶波浪载荷[M].北京:国防工业出版社,2007.

[4]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.

[5]马 山.高速船舶运动与波浪载荷计算的二维半理论研究[D].哈尔滨:哈尔滨工程大学,2005.

[6]DNV,SESAM wasim user manual[K].September,15,2006.

[7]汪雪良.波浪中多体船舶响应的二维理论研究[D].无锡:中国船舶科学研究中心,2006.

[8]毛筱菲.双体船连接桥波浪载荷的试验研究[J].船海工程,2003(6):10-12.