孤立点集及其导集的性质

罗群，张占亮

（肇庆学院数学与信息科学学院，广东肇庆526061）

孤立点集及其导集的性质

罗群，张占亮

（肇庆学院数学与信息科学学院，广东肇庆526061）

归纳出孤立点集及其导集的6个性质；还通过几个实例讨论了孤立点集之导集的可数性问题.

孤立点；导集；Cantor集；可数集；不可数集

在实变函数论中，涉及到孤立点集的结论并不多见.我们知道有限集的导集是空集，实数轴上的有理数集Q虽然是可数集，但其导集Q′＝(－∞,＋∞).那么对于可数的孤立点集而言，其导集的情况如何，孤立点集及其导集具有哪些性质，这些问题有待探究.本文中，笔者主要从可数集、不可数集等方面对孤立点集及其导集的性质进行讨论.

1 基本定义

为了叙述方便，先给出一些基本定义.

定义1若集合A与正整数集Z＋对等，则称A是可数集.有限集与可数集统称为至多可数集.

定义2设E⊂Rn，x∈Rn，若存在δ＞0，使E∩N(x,δ)＝{x}，则称点x是集合E的孤立点.其中Rn表示n维欧氏空间，N(x,δ)表示以点x为心，δ为半径的邻域.如果集合E的每个点都是孤立点，则称E是孤立点集合或孤立集合.

显然集合E的孤立点一定属于E，且是E的边界点.

定义3设E⊂Rn，x∈Rn，若对任意δ＞0，N(x,δ)都含有E的无穷多个点（或N(x,δ)至少含有E的1个异于x的点），则称点x是集合E的聚点.集合E的聚点的全体称为E的导集，记为E′.

显然，集合E的聚点可以属于E，也可以不属于E.

定义4如果集合E的闭包E(E＝E∪E′)没有内点，则称E是疏朗集.

2 孤立点集及其导集的性质

利用孤立点等的定义及相关参考文献[1]17－42,96－150[2]8－28可得到孤立点集及其导集的如下几个性质.

性质1设E⊂Rn，则E－E′是E的孤立点集.

证设x∈E－E′，则点x∈E，但x不是E的聚点.由定义3，存在δ＞0，使N(x,δ)只含E的有限个点.若N(x,δ)只含E的1个点，则E∩N(x,δ)＝{x}，即点x是E的孤立点；若N(x,δ)含有E的2个以上(有限个)点，记这有限个点中异于x的点分别为x1，x2，…，xk，k≥1，取

δ*＝min{d(x,xi)∶i＝1,2,…,k}＞0,

其中d(x,xi)表示点x与点xi的距离（下文皆同），则E∩N(x,δ*)＝{x}，从而点x是集合E的孤立点.结论成立.

性质2设B为集合A的孤立点的全体，则A＝B∪（A′∩A）.

注2性质6反之不真.例如：Cantor集是疏朗集，但Cantor集是完备集不是孤立点集.

3 孤立点集的导集的可数性问题

由于有限集合的导集是空集，所以有限的孤立点集的导集当然也是空集.对于可数的孤立点集，其导集的情况通过几个例子进行说明.

例1设E＝{1,2,3,…}，则显然E是可数的孤立点集，且E′＝∅，此孤立点集是闭集.

上述3个例子说明孤立点集的导集可以是至多可数集；此外，孤立集合的导集还可以是不可数的无穷集.为验证这一结论，下面先介绍Cantor集[1]33－34[2]13－14.

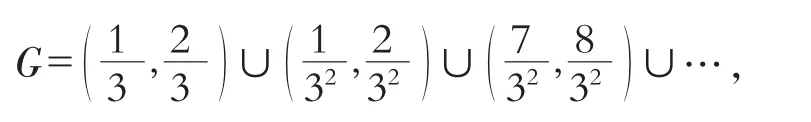
而称P＝[0,1]－G为Cantor集.

Cantor集P是完备的疏朗集且Cantor集P具有连续基数c，当然Cantor集P是不可数的.

例4[2]27设S是Cantor集P在构造过程中去掉的开区间的中点构成的集合，由文献[1]20习题2知S是可数的.下面验证S′＝P，从而.又由于S∩S′＝∅，由性质5知S是孤立点集.

事实上,对任意x∈S′，若x∈[0,1]－P＝G，由G的构造，存在x的某个开邻域N(x)落在G的某一构成区间内，所以(N(x)－{x})∩S＝∅，这与x∈S′矛盾，所以x∈P，从而S′⊂P.反之，设x∈P，∀δ＞0，取正整数n使1/3n＜δ/2，由Cantor集P的构造，第n次去掉的2n－1个开区间中必有1个含于N(x，δ)内.记该开区间的中点为x0，则x0∈S，且x0≠x，于是x0∈(N(x，δ)－{x})∩S.即(N(x，δ)－{x})∩S≠∅，从而x∈S′，P⊂S′.于是S′＝P.

通过如上4个例子可以得知，可数孤立点集的导集可以是空集、非空有限集、可数集和不可数集.

∶

[1]江泽坚,吴智泉,纪有清.实变函数论[M].3版.北京:高等教育出版社,2007.

[2]郑维行,王声望.实变函数与泛函分析概要:第1册[M].北京:人民教育出版社,1980.

(School of Mathematics andInformationSciences,Zhaoqing University,Zhaoqing,Guangdong 526061,China)

The Properties of Isolated Set and Its Derived Set LUOQun,ZHANG Zhanliang

In this paper,six properties of isolated set and its derived set are summed up.And by some examples,the countability of derivedsetof isolatedsetis discussed

isolatedpoint;derivedset;Cantorset;countable set;non-countable set

O174.1

A

1009－8445（2010）05－0005－03

（责任编辑：陈静）

2010－04－13

罗群(1963－)，女，重庆巴县人，肇庆学院数学与信息科学学院教授，博士.