闭区间有限覆盖的算法

江世宏

（武汉工程大学理学院，湖北 武汉 430205）

0 引 言

许多实际问题可抽象成为闭区间（或闭区域）的有限覆盖问题．如，对发生在海洋某区域的海难进行搜救，参与搜救的各种设备（如舰船、飞机、卫星）所能探测范围有限且不同，如何有效地利用这些设备，对疑拟区域进行搜救，是一个利用多种设备的探测区域去覆盖疑拟区域的问题．又如，有m个居民小区，需配置n台信号发射设备覆盖它（m＞n），如何经济地购买与配置n台发射设备，是一个多区域的覆盖问题．有限覆盖定理［1－2］是一个著名的数学定理，它给出了这样一个结论：若开区间集S覆盖闭区间［a，b］，则S中存在有限个开区间也覆盖［a，b］．该定理的证明多为存在性的，并非构造性的，即没有给出覆盖［a，b］的开区间挑选方法．

本文根据贪心法［3－4］，讨论了两种求闭区间有限覆盖的算法，并用计算机对所提出的算法进行了摸拟测试．

1 多个闭区间的覆盖问题

1．1 问题的提出

用i来表示x轴上坐标为［i，i＋1］的闭区间，对于任意给定的m个互异正整数，就有m个这样的闭区间．现在要求画若干条线段覆盖住这些闭区间．其条件是：线段的数目为n，每条线段可以任意长，但要求所画线段的长度之和最小．

1．2 求解分析

将m个互异正整数按升序排序，并存入m维的一维数组p中，讨论如下：

（1）当n≥m时：可用m条长度为1的线段覆盖所有闭区间，线段总长的最小值为m．

（2）当n＝1时：显然，用一条长度为p（m）－p（1）＋1的线段可以覆盖住所有闭区间．

（3）当n＝2时：欲用2条线段覆盖住所有的闭区间，等价于将n＝1时的覆盖线段分为两部分，分别覆盖住左边和右边的闭区间，即在m个闭区间中的某两个不相邻区间之间断开（如图1所示）．

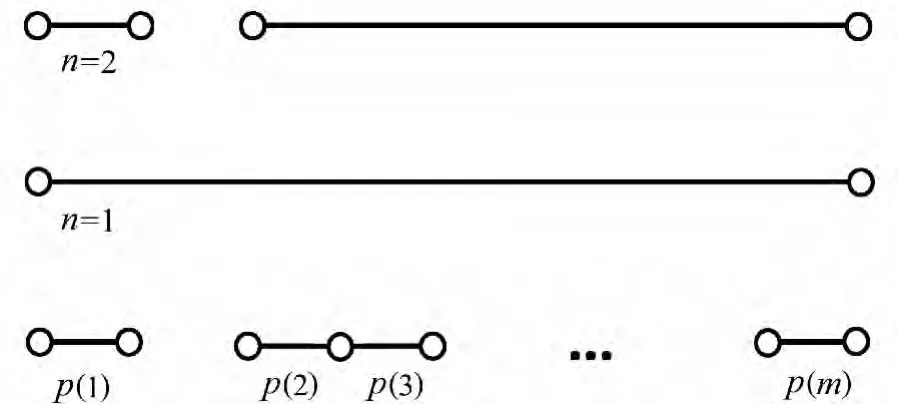
图1 多区间的覆盖方法Fig．1 Method of covering intervals

如果在p（1）与p（2）之间断开，线段的长度将会减少p（2）－p（1）－1．要获得最小的线段总长，需找到间隔距离最大的两个区间，在它们之间断开即寻找d（i）＝p（i＋1）－p（i）－1（1≤i≤m－1）中的最大者．

（4）当n＝3时：应在n＝2时的某种覆盖方案下，将某条线段断成两截，为了得到当前情况下的最小总长，同样应该在间隔最大的两个区间之间断开．如果原方案是n＝2时总长最小的方案，那么这一操作可以得到n＝3时总长最小的方案．

类似地，当n＝k（k＞1）时，只要在n＝k－1时总长最小的覆盖方案下，找到被同一条线段覆盖的间隔最大的两个区间，从间隔处断开，就可以得到n＝k时的最佳覆盖方案．

据上述分析，多区间覆盖问题是一个多阶段决策问题，它满足最优化原理，可运用贪心法来求解．

1．3 算法

步骤一：输入m个互异正整数，作升序排序，存入一维数组p；输入覆盖线段数n．

步骤二：计算两个相邻区间的间隔距离、间隔区间的左右端点，并存入二维数组gap中，即gap（1，i）＝p（i＋1）－p（i）－1，gap（2，i）＝p（i）＋1，gap（3，i）＝p（i＋1）（i＝1，2，…，m－1）．

步骤三：对gap中各列，按第一行作降序排序．

步骤四：如果n≥m，用从p（i）到p（i）＋1的线段覆盖区间（i＝1，2，…，m），输出总长length＝m，线段数num＝m；

步骤五：如果n＝1，用从p（1）到p（m）＋1的线段覆盖区间，输出总长length＝p（m）－p（1）＋1，线段数num＝1；

步骤六：如果2≤n＜m，做以下操作

（1）用从p（1）到p（m）＋1的线段覆盖区间，置总长length＝p（m）－p（1）＋1，线段数num＝1；

（2）当num＜n时，反复做以下操作

①从覆盖线段中，挖去gap（2，num）至gap（3，num）这一段；

②更新线段总长length＝length－gap（1，num）；

③更新线段数num＝num＋1．

（3）输出总长length和线段数num；

在MATLAB下，编写该算法的摸拟检测程序，其程序运行结果如图2所示．

图2 多区间覆盖方法演示程序Fig．2 Program of covering intervals

2 闭区间的有限覆盖问题

2．1 问题的提出

设有闭区间［a，b］和开区间集S＝｛（a1，b1），（a2，b2），…，（an，bn）｝，判断S是否能覆盖［a，b］，如果能覆盖，给出［a，b］的一个有限覆盖，但要求使覆盖的开区间个数最少．

2．2 求解分析

用二维数组I存放开区间集（不妨认为已对I中的第一列作了升序排序），即

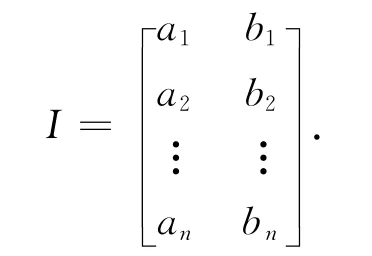
欲覆盖闭区间［a，b］，其关键是如何从开区间集I中挑选出某开区间（ai，bi），覆盖左端点a．为了能用最少的开区间覆盖［a，b］，开区间（ai，bi）应满足条件：ai＜a，bi－a＝di＞0且di最大（这就是贪心策略）．

具体的挑选过程为：在开区间Ii＝（ai，bi）（i＝1，2，…，n）中，做第一轮挑选．对所有的ai＜a，计算di＝bi－a，存在着dr＝max｛di｝，选出开区间Ir＝（ar，br），它具有以下3种情况之一（如图3所示）．情况1：dr≤0，Ir未覆盖a；情况2：dr＞b－a，Ir覆盖a，且覆盖［a，b］；情况3：0＜dr≤b－a，Ir覆盖a，未覆盖［a，b］．

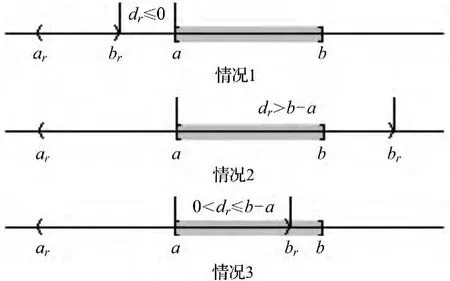
图3 首选开区间的3种可能情况Fig．3 Three cases of first opened interval

对于情况1，可以断言，在开区间集I中，无法挑选出有限个开区间，实现对［a，b］的覆盖；对于情况2，可以断言，开区间Ir＝（ar，br）已实现对［a，b］的覆盖；对于情况3，取a＝br，缩小［a，b］，再从开区间Ii＝（ai，bi）（i＝r＋1，r＋2，…，n）中，做新一轮的挑选．

2．3 算法

步骤一：输入［a，b］，I．

步骤二：获取I中开区间个数n，对I中第1列作升序排序．

步骤三：置所选开区间个数m＝0，取j＝1（即从I中第j＝1个开区间开始进行挑选）．

步骤四：当j≤n时，反复做以下操作：

（1）d＝0（所选开区间对a的覆盖距离赋初值），r＝0（所选开区间序号赋初值）．

（2）对于i＝j，j＋1，…，n，反复做以下操作

如果I（i，1）＜a且I（i，2）－a＞d，则d＝I（i，2）－a，r＝i

（3）如果r＞0，则m＝m＋1，S（m，1）＝I（r，1），S（m，2）＝I（r，2）

（4）如果d＝0，则标识变量flag＝0，退出挑选操作．

（5）如果d＞b－a，则标识变量flag＝1，退出挑选操作．

（6）如果0＜d≤b－a，则a＝I（r，2），j＝r＋1，返回第4步．

步骤五：如果flag＝0，输出“不能覆盖”信息；否则，输出“可以覆盖”信息，并输出S中所存储的m个开区间．

在MATLAB下，编写该算法的模拟检测程序，其程序运行结果如图4所示．

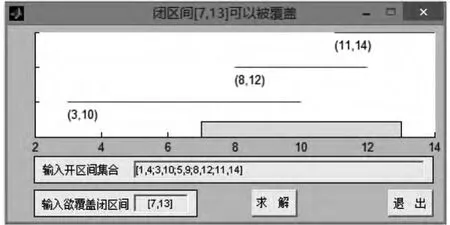
图4 闭区间覆盖方法演示程序Fig．4 Program of covering closed interval

3 结 语

闭区间有限覆盖问题，在经济、管理、军事、计算机和数学领域里，具有十分广泛的应用，对该问题的研究，有待进一步深化．例如，还可以讨论，在要求所有覆盖闭区间的开区间总长最小的条件下，算法的设计问题．

致谢

感谢国家科技部和武汉工程大学对本项目的资助！

［1］郭改慧，李兵方．有限覆盖定理的应用［J］．牡丹江大学学报，2013，22（10）：103－104．

［2］关金玉，徐永春，祁建芳．用完全覆盖证明实数系中若干定理［J］．河北北方学院学报：自然科学版，2006，22（3）：6－7．GUAN Jin－yu，XU Yong－chun，QI Jian－fang．To prove several theorems in real number field by using full covering theorem［J］．Journal of Hebei North University：Natural Science Edition，2006，22（3）：6－7．（in Chinese）

［3］常友渠，肖贵元，曾敏．贪心算法的探讨与研究［J］．重庆电力高等专科学校学报，2008，13（3）：41－42，47．CHANG You－qu，XIAO Gui－yuan，ZENG Min．Exploration of greedy algorithm ［J］．Journal of Chongqing Electric Power College，2008，13（3）：41－42，47．（in Chinese）

［4］崔鹏，刘红静．测试集问题的综合覆盖贪心算法的深入近似［J］．软件学报，2006，17（7）：1494－1500．CUI Peng，LIU Hong－jing．Deep approximation of set cover greedy algorithm for test set［J］．Journal of Software，2006，17（7）：1494－1500．（in Chinese）