实变函数中集合外测度三种定义的等价性

胡永模，周其生

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)



实变函数中集合外测度三种定义的等价性

胡永模，周其生

(安庆师范学院 数学与计算科学学院，安徽 安庆 246133)

摘要：本文列出了实变函数中集合外测度的三个常见的定义，并对其之间的等价性给出了证明。通过这三种定义证明了外测度的一些基本性质，从而更好地揭示外测度这一概念的内涵。

关键词：外测度；开区间；开集；可测集

实变函数论中核心的内容之一是建立在测度理论上的勒贝格积分理论，而测度理论的核心是建立一般集合外测度。因而集合外测度概念是实变函数中的一个基本概念。目前实变函数论的各种教材中定义的集合外测度概念都是用开区间的长度(面积，体积)来定义的，即

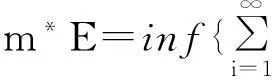
Ii为有限区间，i=1,2,…}

(1)

在本文中我们分别通过开集以及可测集的测度来给出一般集合勒贝格外测度的另外两种定义形式并对其等价性给出证明。

1外测度另外两种定义

定义1设E⊂Rn，则称

m*E=inf{m(O)|O为开集，且O⊃E}

(2)

为E的外测度。

定义2设E⊂Rn，则称

m*E=inf{m(A)|A为可测集，且A⊃E}

(3)

为E的外测度。

2三种定义间的等价性的证明

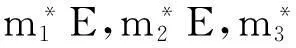
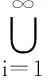
inf{m(O)|O为开集且O⊃E}≤

即

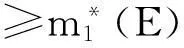
即

证明(2)式与(3)式的等价性事实上，由于开集一定为可测集，所以，

{O|O为开集且O⊃E}⊂{A|A为可测集且A⊃E}

所以，{m(O)|O为开集且O⊃E}⊂{m(A)|A为可测集且A⊃E}，所以，inf{m(O)|O为开集且O⊃E}≥inf{m(A)|A为可测集且A⊃E}

即

在绿色西江建设方面，深化“政、企、军”船舶防污染应急合作共建工作。完善西江水上突发事件队伍共建机制，深化西江水上突发事件应急资源共享机制，提升西江溢油应急响应速度。

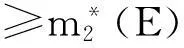
所以

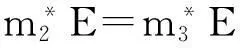
3应用实例

用以上等价定义来证明下列三条基本性质：

1)m*E≥0，当E为空集时，m*E=0；

2)单调性，设A⊂B，则m*A≤m*B；

3.1用(1)式来证明这三条性质

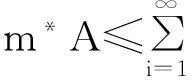
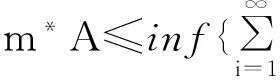
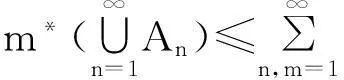
3.2用(2)式证明这三条性质

①基本性质1 显然成立；

②基本性质2的证明：设A⊂B，O为一覆盖B的开集，则O一定覆盖A，因而m*A≤m(O)，所以

m*A≤inf{m(O)|O为开集且O⊃B}≤m*B

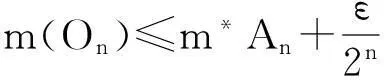
3.3用(3)式来证明这三条性质

①基本性质1 显然成立；

②基本性质2的证明：设A⊂B，E为可测集，且E覆盖B，则E一定覆盖A，因而m*A≤mE，即

m*A≤inf(mE)=m*B

所以m*A≤m*B

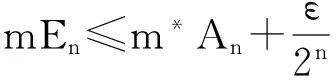
4几点评注

可测函数的上述三种定义，尽管等价但各有优点和缺陷。

(1)传统外测度定义是从区间的长度(面积，体积)的角度描述的。该定义比较自然，且简捷明快，容易跟数学分析中区间的长度(平面与空间区域的面积与体积)作比较，使学生懂得外测度实际上是长度(面积，体积)的推广，故易于理解和接受。但这一定义不易刻画后续章节中可测集的结构，可能易将点集的可测性与函数的可测性相混淆。

(2)另外两种定义是从不同的逼近角度，利用集合的开集与可测集的逼近定理来刻画集合的外测度。 该定义容易刻画后续章节中可测集的结构,这使得我们把握住了可测集的结构和实质。但这两个定义比较抽象，不容易跟数学分析中区间的长度(平面与空间区域的面积与体积)作比较，故学生理解起来困难。

参考文献:

[1] 程其襄, 张奠宙, 魏国强, 等. 实变函数与泛函分析基础[M].第2版.北京: 高等教育出版社, 2003.

[2] 江泽坚, 吴志泉.实变函数论[M].北京: 高等教育出版社, 1994.

[3] 吴炯圻, 周戈. 实变与泛函——基本原理与思想方法[M]. 厦门：厦门大学出版社, 2004.

[4] 夏道行, 吴卓人, 严绍宗, 等. 实变函数与泛函分析(上册)[M]. 北京：人民教育出版社, 1987.

[5] W.Rudin. Real and complex analysis[M]. New York: McGraw-Hill, 1966.

Equivalence of Three Definitions about Exterior Measure in Real Variable Function

HU Yong-mo, ZHOU Qi-sheng

(Department of mathematics and computational science, Anqing Teachers College, Anqing 246133,China)

Abstract:In this paper, we set out three ordinary definitions of exterior measure and prove their mutual equivalence. In addition,we prove some exterior measure's basic properties by using the three definitions.So the concept essence of exterior measure can be better showed.

Key words:exterior measure,open interval,open set,measurable set

文章编号：1007-4260(2015)03-0107-03

中图分类号：O174.1

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2015.03.028

作者简介：胡永模，男，安徽无为人，硕士，安庆师范学院数学与计算科学学院讲师，研究方向为算子理论与算子代数。

基金项目：安庆师范学院校级青年科研项目(KJ201106)，安徽省质量工程项目(2012gxko75)省级精品资源共享课程《实变函数》。

收稿日期：2014-07-16

网络出版时间：2015-8-25 15:40网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.028.html