自然气象条件下某型吸波涂料静态吸波能力变化模型建立

逄剑峰，李淑华

（海军航空工程学院青岛分院，山东青岛，266041）

自然气象条件下某型吸波涂料静态吸波能力变化模型建立

逄剑峰，李淑华

（海军航空工程学院青岛分院，山东青岛，266041）

研究了自然气象条件下单层碳纤维吸波涂料的静态吸波性能随时间变化的规律。通过人工加速老化试验模拟自然气象分周期作用于吸波材料试样，然后测量其电磁参数与反射率，并对实验数据进行处理，结合由电磁参数计算反射率模型的理论推导，最终建立了试样的反射率随时间变化模型，并依此预测此涂料的使用寿命，为确定其在隐身飞行器上的使用与维护时限提供依据。

碳纤维；RAM；模型

现代意义上的隐身技术起源于二战中雷达侦察与对抗，发展于上世纪六、七十年代的美苏冷战阶段，在八十年代后期走向成熟。隐身飞机首次参加实战是在海湾战争期间，它的出现极大程度地改变了空军作战模式，是二战以来人类最伟大的军事技术创新之一。

隐身技术的方法很多，其中，在飞行器外表面涂覆吸波涂料的方法被现役的隐身飞行器所广泛采用。由于吸波涂料是直接暴露于自然气象环境当中的，大气中的阳光、氧气、温度变化、降水、盐雾等等都会对吸波涂料产生不同程度的影响，这些影响一方面是物理特性上的，比如说涂层开裂、变形、变色、局部脱落等；另一方面是电磁特性上的，即改变材料的电磁参数（主要是复介电常数和复磁导率）。两者都会对涂料的吸波性能造成影响：变差的表面会增强电磁波的散射，局部脱落处更是会丧失吸波能力；变化的电磁参数会改变设计之初的吸波方案，而合理的电磁参数配置是吸波材料良好吸波性能的保证。吸波涂料表面变差对吸波性能的影响不是本文要研究的，本文是在保证吸波材料表面无过大程度变化的情况下，研究电磁参数的变化对于吸波涂料吸波性能的影响。

因为不同的吸波涂料使用不同的雷达波吸收剂，或有着不同层数以及不同吸波剂和黏结剂混合比例，所以可以说每一种吸波涂料都是独一无二的，在自然气象条件下吸波能力的变化规律都不会完全一样。这里我们以单层碳纤维吸波涂料为例建立吸波材料吸波性能随时间变化的模型。

1 碳纤维吸波材料

碳纤维、碳黑和石墨都属于碳系吸波材料，都是非磁性吸收剂，故它们的复数相对磁导率实部为1，虚部为零，即μ′=1，μ″=0。碳纤维是由有机纤维或低分子烃类气体原料加热至1500℃所形成的纤维状碳材料，其碳含量为90％以上，它是不完全的石墨结晶沿纤维轴向排列的物质，各平行层原子堆积不规则，缺乏三维有序，呈乱层结构。碳纤维层面主要是以碳原子共价键相结合，而层与层之间是以范德华力相连接，因此碳纤维是各项异性材料。碳纤维具有低密度、高强度、高模量、耐高温、低电阻、低膨胀等优良特性［1］。

碳纤维的吸波机理为导电损耗，在制成吸波涂层后，RAM内部存在相互联系的导电载流子，在电场作用下，这些导电载流子将作定向漂移，在RAM内形成传导电流，这部分电流将以热的形式消耗掉。

碳系吸波涂料的优点是密度小，价格便宜，做成的涂料控制在半导体量级时可以得到较好的吸波性能；缺点是低含量时电损耗角正切值较小，高含量时虽然损耗会增大，但加工会比较困难，力学性能也会受到影响。此外，碳系涂料的表面含有羟基、羰基等活性基团，可以同高分子材料发生反应，这也是碳系吸波材料发生老化的一个重要原因。

本实验所用的吸波材料测试样板由上海某公司制作提供。该测试样板由吸波材料喷涂在表面光滑的铝板上制得，雷达吸收剂为一种短切碳纤维（平均长度为3mm），黏结剂为氟硅树脂；样板中碳纤维的体积分数为30％，涂层厚度为2mm。

除了测试样板外，还要有一段加工于波导内的吸波材料试样用来测试吸波材料的电磁参数，此试样采用和样板完全一样的材料。

2 单层碳纤维吸波材料反射率计算模型

根据电磁波传输理论，电磁波在波阻抗不同的两种介质中传输必然会存在着反射。当电磁波垂直入射时，吸波材料与空气形成的界面的反射率为［2］：

式（2）中η是吸波材料的归一化特性阻抗：

式（1）、（2）中k是电磁波在材料中的传播常数，可表示为：

式（3）、（4）中，ε为材料的相对复介电参数，ε=ε′-jε″（ε′、ε″分别为吸波材料相对复介电参数的实部与虚部）；μ为材料的相对复磁导率，μ=μ′-jμ″（μ′、μ″分别为吸波材料相对复磁导率的实部与虚部）；σ为材料的电导率；d为涂料层的厚度；f为电磁波频率；ω=2πf为角频率；c为光速。

实际上，许多介质参数的测量并不单独去测量电导率，因为它已经体现在ε″中［3］，故式（3）和式（4）可以简化成：

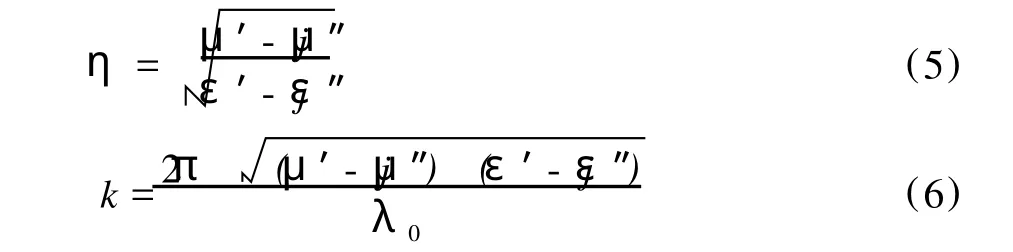
则

当把吸波材料的复电磁参数带入（7）式时就可以计算出输入阻抗，再将输入阻抗带入（1）式就得到该吸波涂料的反射率：

用分贝单位表示功率反射率为：

对于本实验所用的测试样板来说，因为所用雷达波吸收剂为导电损耗型的碳纤维，它的μ′=1，μ″=0，且黏结剂的磁损耗小到可以忽略，所以将二者代入反射率计算公式（9），得：

上式是关于频率f、涂层厚度d、材料复相对介电常数ε的函数，而ε又随f的变化而变化。为了研究的方便，选定X波段的某个固定频率，10.5GHz，作为研究对象。对于已经做好的样板，样板厚度d也是一个固定值。若能找到材料的相对介电常数ε随时间变化的规律，就可以求得本RAM样板的反射率随时间变化的规律。

3 相关实验

相关实验分为三项内容，一是吸波材料测试样板的反射率测量实验，二是吸波材料波导试样的电磁参数测量实验，三是人工加速老化试验。实验分成若干个周期进行，每个周期的前半部分实验样品要放入老化实验箱中进行人工加速老化，在后半部分取出实验样品测试其电磁参数和反射率，完成后进入下一个实验周期。实验期间，需要将测试样板与波导试样一起放置在老化实验箱中，合理设置实验条件，在每个实验周期模拟正常条件下一个月的自然气象条件（限于实验条件，主要是日照、降雨两项），然后测量样板的反射率与波导试样的电磁参数，最后将12个实验周期（模拟一年的自然环境）的数据汇总。

实验当中，波导试样的制作要求是：采用与吸波涂料测试样板完全一致的材料，制作厚度也为2mm，且保证在老化试验时与测试样板经受同样的人工加速老化环境，这样由波导试样测得的涂料电磁参数及其变化规律就同测试样板上的吸波涂层电磁参数及其变化规律完全一致。

吸波样板的反射率采用弓形法测量，波导试样的电磁参数由传输/反射法测量得到，人工加速老化试验在氙灯耐候试验箱内进行。

4 实验数据分析与曲线拟合

表1是实验测得的碳纤维波导试样在不同的实验周期测试得到的相对复介电参数（相对磁导率近似为μ=1-0i，未给出）、反射率数值以及用测得的电磁参数计算所得样板反射率的值。

表1 RAM样板在不同实验周期的相对复介电参数、计算以及实测反射率Table 1 The relative per mittivity data and reflectivity data of RAM sample computed and measured in every period

因为几条参数曲线的走势都接近线性，故实验数据采用MAT LAB软件进行线性回归处理，并对回归效果进行检验。这里采用的是F检验法，只给出检验结果，具体内容不再详述，请参考文献［4］。

（1）相对介电参数实部回归方程。

图1 相对介电参数实部数据、拟合曲线与误差图Fig.1 The curve fitting of real part of relative permittivity

图1为实验在不同周期测得的RAM相对介电参数的实部和经MATLAB处理后得到的回归方程，以及两者之间的差异值。

线性回归得到的方程为y1=12.3-0.108t，其中t为实验周期，y1表示相对介电参数的实部。对线性回归效果进行检验，有：

F=189.92＞F0.001（1，11）=19.69

所以，将相对介电参数的实部回归成函数y1=12.3-0.108t效果显著，所得方程有效。

（2）相对介电参数虚部回归方程。

图2 相对介电参数虚部、拟合曲线与误差图Fig.2 The curve fitting of imaginary part of relative permitivity

图2为实验在不同周期测得的RAM复相对介电参数的虚部和经MATLAB处理后得到的回归方程，以及两者之间的差异值。

线性回归得到的方程为y2=3.22-0.105t；其中t为实验周期，y2表示相对介电参数的虚部。对线性回归效果进行检验，有：

F=570.87＞F0.001（1，11）=19.69

所以，将相对介电参数的虚部拟合成函数y2=3.22-0.105t效果显著，所得方程有效。

（3）计算所得反射率回归方程。

图3 计算反射率数据、拟合曲线图及误差图Fig.3 The curve fitting of computed reflectivity

图3为实验在不同周期测得的RAM电磁参数经（10）式计算所得反射率和经MATLAB处理后得到的回归方程，以及两者之间的差异值。

线性回归得到的方程为R1=-14.4+0.412t；其中t为实验周期，R1表示计算所得反射率数值。对线性回归效果进行检验，有：

F=124.27＞F0.001（1，11）=19.69

所以，将由测量得到的相对介电参数计算反射率回归成函数R1=-14.4+0.412t效果显著，所得方程有效。

（4）实测反射率回归方程。

图4 实测反射率数据、拟合曲线图及误差图Fig.4 The curve fitting ofmeasured reflectivity

图4为实验在不同周期实测的RAM反射率和经MATLAB处理后得到的回归方程，以及两者之间的差异值。

线性回归得到的方程为R2=-13.6+0.292t；其中t为实验周期，R2表示实测所得反射率数值。对线性回归效果进行检验，有：

F=249.94＞F0.001（1，11）=19.69

所以，将实测反射率回归成函数R2=-13.6+0.292t效果显著，所得方程有效。

比较计算所得反射率回归出来的函数R1=-14.4+0.412t和实测反射率所回归出来的函数R2=-13.6+0.292t，在t=0到t=12的范围内，两者最大相差0.8dB，相差百分比为（0.8/13.6）×100％=5.88％，较为理想，可以视为计算所得反射率与实测反射率相近，证明可以用电磁参数随时间变化的规律来表示反射率随时间变化的规律，即可用回归的电磁参数方程代入反射率模型（10）得到反射率随时间变化的模型。

本实验样板最终的反射率随时间变化的模型为：

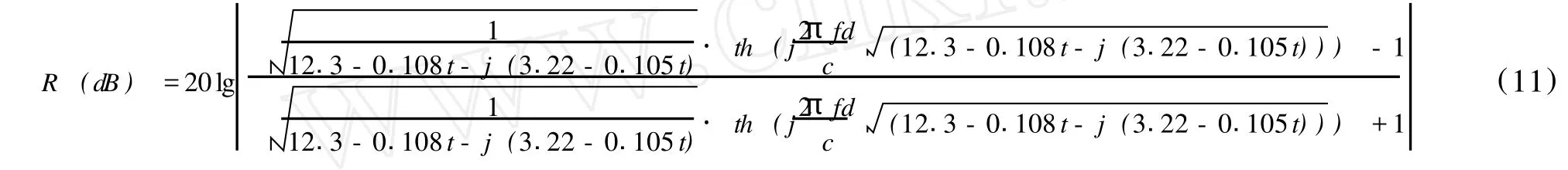
其中，t为时间，c为光速，d为涂料层的厚度，f为实验中测试时使用的电磁波频率。为了扩大模型的适用范围，实际应用时，f应选择为所要对抗雷达工作频率的中心频率。

依此模型计算，当t=10.25时，即实验样品在自然环境下放置10.25个月后，在10.5GHz频率下吸波涂料的吸收率将降到-10dB左右，此时可以认为吸波材料在此频率下的吸波性能已经下降到不能容忍的地步，需要进行修复。

5 结论

（1）可以通过观察吸波材料复电磁参数随时间变化规律来推导吸波材料的反射率随时间变化规律。进而建立在某频率下涂层吸波性能随时间变化的模型。

（2）可将人工加速老化试验引入吸波材料在自然气象条件下性能变化的研究。

（3）模型计算结果与实测结果两者经过相互印证表明能够较好地符合，证明了本实验过程的可行性。

［1］王钧，刘东，王翔，杨小利.碳纤维在功能复合材料中的应用［J］.国外建材科技，2002，23（2）：6-8.

［2］胡传析.隐身涂层技术［M］.北京：化学工业出版社，204-206.

［3］中国人民解放军总装备部.GJB 5239-2004射频吸波材料吸波性能测试方法［S］.北京：总装备部军标出版发行部，2004，9.

［4］沙定国.误差分析与测量不确定度评定［M］.北京：中国计量出版社，176-178.

Model-building of the Change of Static Electromagnetic Wave Absorbing Performance of Some RAM in the Natural Environment

PANG Jian-feng，LI Shu-hua
（Qingdao Branch Naval Aeronautical Engineering Institute，Qingdao 266041，Shandong，China）

The static electromagnetic wave absorbing performance of the RAM which consists of single coat of carbon fiber in the natural environmentwas studied.Artificial aging exper imentwas performed on test board，then the electromagnetic parameters and reflectivity of it were measured，combing with the derivation of the model in which the reflectivity can be calculated with electromagnetic parameters，to build the model of reflectivity changing over time.It is used to forecast the natural life of the RAM coats used on the surface of stealth aircrafts.

carbon fiber；RAM；model

E919

2009-10-12