线性规划法在水资源系统规划优化配置中的应用

康永辉，王宝红

（广西水利电力勘测设计研究院，广西 南宁 530023）

1 线性规划简介

线性规划是运筹学中应用最为广泛的一个分支，也是运筹学最基本的部分。线性规划是研究在现有人力、物力等资源条件下，合理调配和有效使用资源，以达到最优目标（产量最高、利润最大、成本最小、资源消耗最少等）的一种数学方法。目前已广泛应用于生产管理、资源分配、运输问题、生产计划问题、环境保护、军事等众多领域。线性规划的数学理论成熟、建模简单，有通用算法和计算机软件进行计算。一般首先根据研究问题的性质确定决策变量；根据问题的目标，列出与决策变量有关的目标函数；根据问题的限制条件，列出与决策变量有关的约束条件来建立数学模型。线性规划的求解有图解法和单纯形法，在实际应用中一般采用单纯形法进行求解。

2 线性规划模型及求解

线性规划模型一般由3个要素组成：①变量，或称决策变量，是问题中要确定的未知量，它用以表明规划中的用数量表示的方案、措施，可由决策者决定和控制；②目标函数，它是决策变量的函数，按优化目标分别在这个函数前加上 max或min；③约束条件，指决策变量取值时受到的各种资源条件的限制，通常表达为含决策变量的等式或不等式。

线性规划模型可以表示为：

（1）求和形式：

（2）矩阵形式：

（3）集合形式：

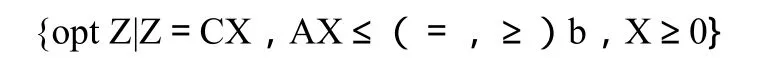
其中：“s.t”（subject to的缩写）表示约束于；“opt”表示最优的意思，一般是max或min。

求解一般线性规划问题有图解法和单纯形法。图解法是求解线性规划的一种直观方法，可用于解决含有两个决策变量的线性规划问题，其目的是判别线性规划问题的求解结局和存在最有解的条件下，把问题的最有解找出来。图解法的步骤可概括为：在平面上建立直角坐标系，两个坐标轴对应于两个决策变量；图示约束条件，找出可行域；图示目标函数和寻找最优解。

根据线性规划解的基本定理，线性规划问题的可行域为凸集或无界域（如果可行域不为空集）；凸集有有限个顶点，每个基可行解对应于一个顶点；若线性规划模型有最优解，必定在某个顶点上取得。对于决策变量数n、约束方程数m比较小的情况，可以采取枚举法，通过比较有限个基可行解的目标函数值来确定最优解与最优值。但对于 n、m比较大的情况，完全枚举法的计算量较大，这就需要采用更有效的方法——单纯形法（simplex method）来求解线性规划模型。

单纯形法的求解思路是：对于给定的 LP模型，从某个基可行解（可行域的一个顶点）开始，按照一定的规则转换到另一个基可行解（顶点），使新顶点的目标函数值优于原目标函数值，经过有限次迭代直至目标函数达到最优。需要解决3个关键问题：初始基可行解（顶点）的确定；基可行解的转换规则；最优行判断准则。单纯形法的计算步骤主要包括：①将 LP模型转换为标准型；②求初始基可行解，列出初始单纯形表；③求得初始基可行解后进入迭代过程，在每一次迭代过程中还包括根据最优性条件确定最优解或换入变量和根据可行性条件确定换出变量两步。确定新的基可行解后继续进行迭代，经过有限次迭代后就可以找到最优解。

3 用线性规划模型优化配置水资源

某供水工程年供水能力为6 500万m3，主要用于工业、农业以及生活用水，有关需水量、水价、供水成本、供水要求见表 1。由于向不同部门供水的水价以及供水成本不一样，因此利润也不样，在满足供水要求的情况，就需确定最优配水方案，才能使供水效益最大。

3.1 决策变量的确立

主要向工业、农业、生活三部门供水，因而可确定工业、农业、生活用水量为决策变量，分别为X1、X2、X3。

表1 需水量、水价、供水成本、供水要求表

3.2 目标函数的建立

根据有关部门的用水量要求，以及水价和成本来确定最优分配方案，使供水效益最大，即Max Z＝（2.8－1.5）X1＋（0.6－0.25）X2＋（2.0－0.6）X3。

3.3 约束方程

（1）三部门的总用水量小于供水工程总供水量，即：

X1＋X2＋X3≤6 500

（2）三部门的最大用水量限制

X1≤3 000，X2≤5 000，X3≤1 000。

（3）三部门的最小用水量限制

X1≥0，X2≥3 000，X3≥0。

3.4 求解

由于该模型含有3个决策变量，不便于用图解法来求解，可采用单纯形法来求解，按照单纯形法的求解步骤及要求可求得目标值为5 700万元，达到最优解时的各变量值分别为：X1＝2 500万m3、X2＝3 000 万 m3、X3＝1 000 万 m3。也可以利用 Microsoft Excel 规划求解工具进行规划求解，Microsoft Excel 规划求解工具可用于求解一定限制条件下目标单元的最大值、最小值及相应的可变单元（决策变量）值，规划求解工具具有数据输入直观、简单、计算快捷，并可生成完整的求解报告等特点。

4 结论及建议

水资源规划目的是根据经济社会可持续发展和环境保护对水资源的要求，提出水资源合理开发、优化配置、高效利用、有效保护和综合治理的总体布局及实施方案，促进我国人口、资源、环境和经济的协调发展，以水资源的可持续利用支持经济社会的可持续发展。

水资源规划是全面落实国家或地区实施可持续发展战略的要求，适应经济社会发展和水资源的时空动态变化，着力缓解水资源短缺、水环境恶化等水问题的一项重要工作。它是根据国家或地区的社会、经济、资源和环境总体发展规划，以区域水文特征及水资源状况为基础来进行的。

通过对线性规划的介绍与实例分析，线性规划的建模过程简单，首先是明确模型的目标函数和约束方程，然后根据线性规划解的求解方法和过程，很容易得到模型的全局最优解。从结果可以看出，在满足供水要求的前提下，供水效益最大，从而为水资源的合理配置提供了理论依据和基础。但在生产实践中，目标函数与约束条件往往不是决策变量的线性函数，为了解决生产实际中的问题，往往还需要用到非线性规划法、动态规划法以及人工神经网络的应用，满足水资源优化配置的更高要求。