加筋结构非节点连接建模中钢筋单元划分方法研究

彭 毅，王家林，易志坚，李 平

(重庆交通大学土木建筑学院，重庆400074)

目前，加筋结构的有限元建模方法主要有分离式、整体式和组合式3种［1］。

分离式模型对加筋结构和基体材料分别划分单元，通过节点连接重构整体。在建模过程中，分离式模型要求加筋单元和基体材料单元共用节点，建模难度大，可能造成两个结果的出现:①加筋构件的布置与实际不符，在计算结果上出现虚假的应力集中;②基体单元的形状不规则［2］，导致计算结果不准确。

整体式模型将加筋构件均匀弥散于整个基体材料单元中，通过各方向的配筋率来计算加筋构件对基体材料的增强效果。这种方法计算简便，但是对加筋构件的布置细节反应不足，更无法模拟有滑移的情况。

组合式模型克服了分离式模型建模难度大和整体式模型过于粗略的特点，为加筋结构的有限元分析提供了一种切实可行的方法。但是，组合式单元模型要求加筋单元与基体材料单元位移连续、变形协调，当两者之间存在位移不连续时，组合式难于处理［3］。

针对以上3种有限元建模方法各自存在的不足，王家林［4］提出了具有一般意义的不通过节点连接的有限元建模和分析方法，即非节点连接方法，并开发了以非节点连接有限元理论为基础的有限元软件RCF。非节点连接方法在处理加筋结构的问题时，可以方便的模拟加筋构件的黏接滑移问题。本文针对加筋结构中钢筋单元跨越多个混凝土单元的情况，在非节点连接理论的框架内分析了筋元与混凝土单元的位置关系，并对筋元与混凝土单元面的交点建立了数学模型，解决了钢筋单元与混凝土单元之间的位移协调问题。

1 筋元与混凝土单元位置关系分析

在加筋结构模型中，一个钢筋单元跨越两个或多个混凝土单元的现象较为常见。由于一个筋单元跨越两个混凝土单元是最基本的筋元跨越问题，因此，有必要对这一问题进行细致分析。

如图1，筋单元AB跨越混凝土单元①及混凝土单元②。筋元A节点作为混凝土单元①的内节点进行分析，筋元B节点作为混凝土单元②的内节点进行分析，在非节点连接理论中，内节点位移由母单元各节点位移插值决定。由于筋元内部各处位移由筋元两端节点位移插值得到，而筋元两端节点又作为混凝土单元内节点，因此，AB段钢筋单元内各处的位移由两个混凝土单元的节点位移插值决定［5］。

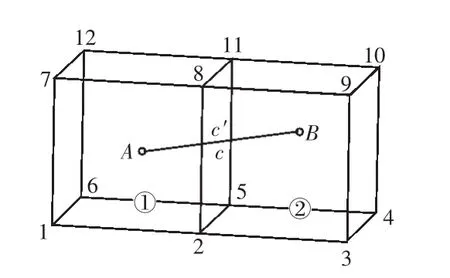
图1 加筋结构单元模型Fig.1 The element model of reinforced structures

在筋元与混凝土单元面的相交处，筋元上的C点与混凝土单元面上C′点重合。C点位移由混凝土单元①和混凝土单元②的各节点位移共同插值决定，C′点的位移由两混凝土单元交面各节点位移插值决定，这使得筋元与混凝土单元之间的位移存在一定的不协调性。

为改善上述不协调性，可以设置筋元上的C点为混凝土单元的内节点。作为钢筋单元与混凝土单元面的交点，C节点既可以作为其左侧混凝土单元①的内节点又可以作为其右侧混凝土单元②的内节点。由于单元面上各点的位移仅与单元面各节点的位移有关，因此无论将C节点作为哪个单元的内节点，均不会产生差别。

C节点的引入，使得原有的一个钢筋单元AB被划分成两个单元，即钢筋AC单元和钢筋CB单元，如图2。钢筋AC单元包含于混凝土单元①内，钢筋CB单元包含于混凝土单元②内。

图2 钢筋设置交点以后的结构单元模型Fig.2 The steel element interpolating a intersection

经过插入节点分段后，AC段筋元内的位移由其所在的混凝土单元①各节点位移插值决定，CB段筋元内的位移由其所在的混凝土单元②各节点位移插值决定，由此，钢筋单元与混凝土单元的位移插值关系便满足了位移的协调性要求。

2 筋元与混凝土单元位置关系

混凝土单元作为等参元，其体内未知点的位移由单元形函数插值得到。对筋单元的数值模拟一般采用线性插值［6］。筋元与混凝土单元相交情况如图3。

图3 筋元与混凝土等参元相交模拟Fig.3 The intersection simulation of steel element and concrete element

由关键点 A(xm，ym，zm)，B(xn，yn，zn)所确定的钢筋段的参数方程为:

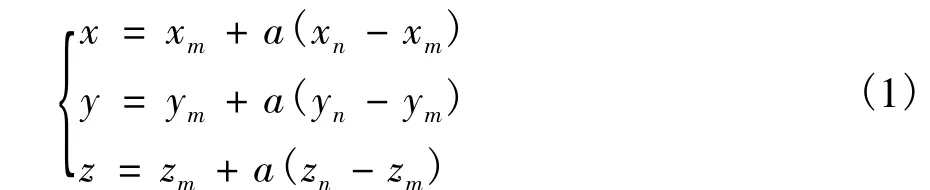
a∈［0，1］，为钢筋单元位置参数。

混凝土等参元坐标变换方程为:

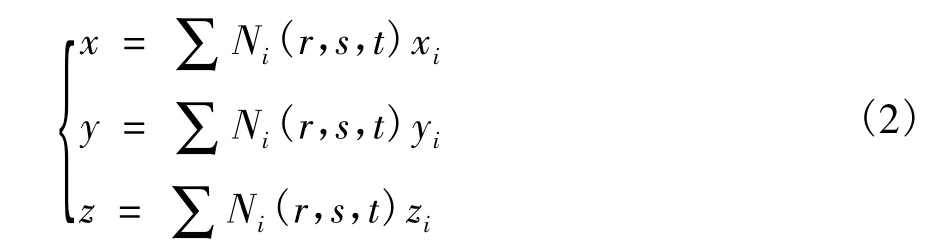
Ni(r，s，t)为混凝土单元内i节点的形函数。

xi，yi，zi为混凝土单元 i节点的位移。

在求钢筋单元与混凝土单元面交点的过程中，将两参数方程联立求解可得到交点坐标:

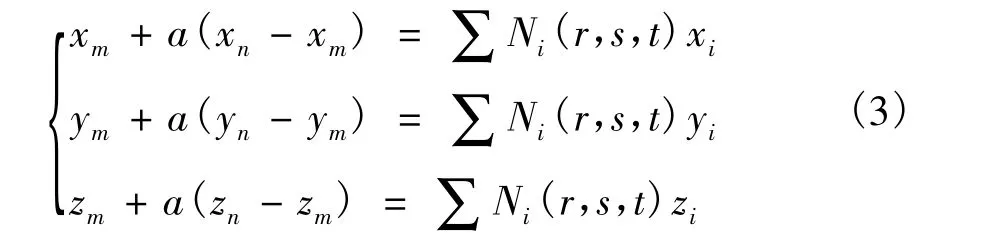
其中，r∈［－1，+1］;s∈［－1，+1］;t∈［－1，+1］，任一参数取+1或－1表示某一单元面。

以求解钢筋与混凝土等参元几何面r=1上的交点为例。

令:

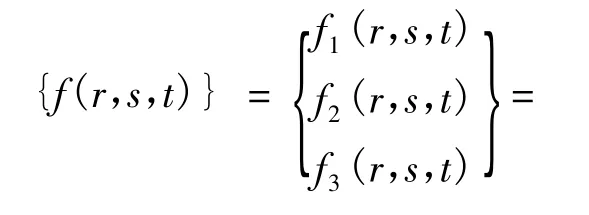
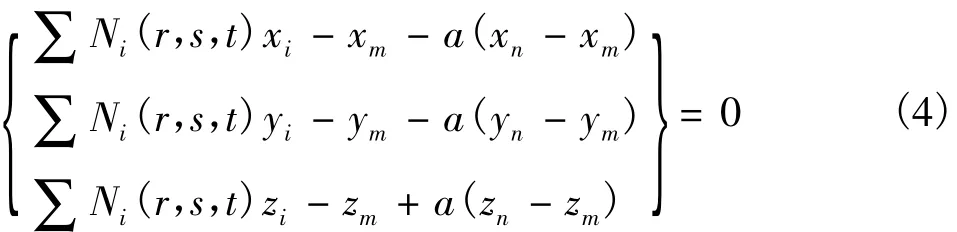
设(sn，tn，an)为方程的第 n 次近似解，将 {f(r，s，t)} 在 (sn，tn，an)处近似展开得:

于是得到下面递推公式:

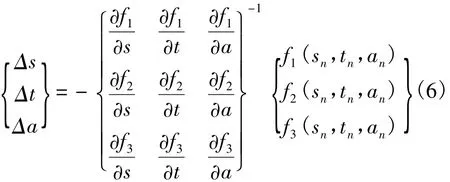
也即:

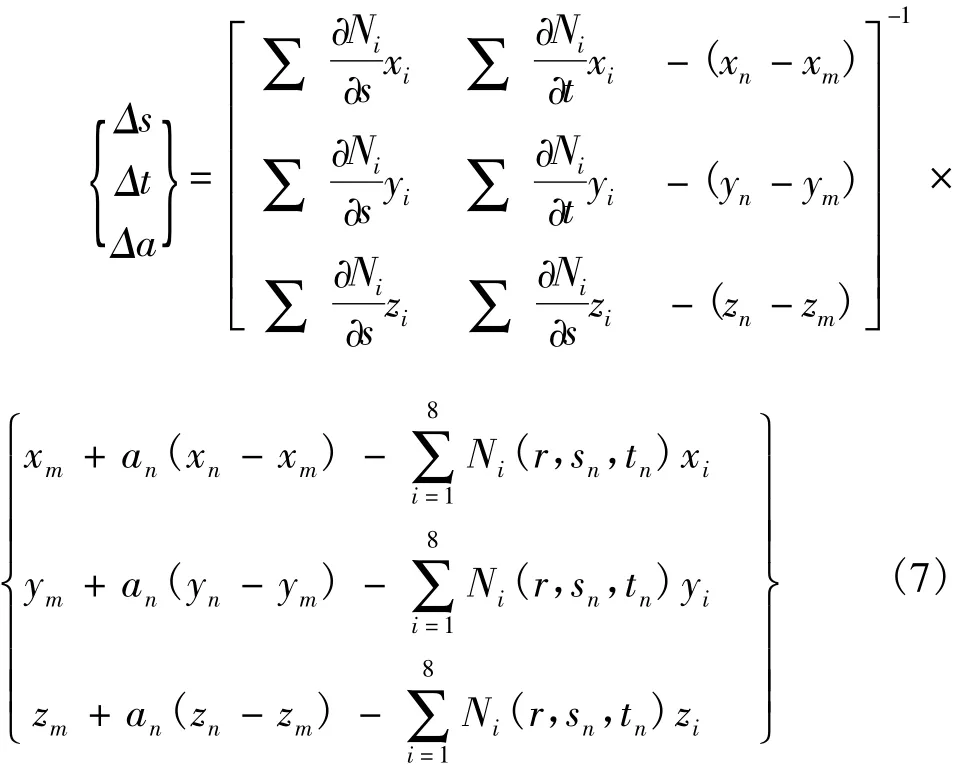
由式(7)，通过迭代计算可得到钢筋与混凝土单元面交点的局部坐标(r，sn+Δs，tn+Δt)以及交点在钢筋直线方程中的比例系数(an+Δa)。

再通过混凝土等参元坐标转换方程得到交点的整体坐标:

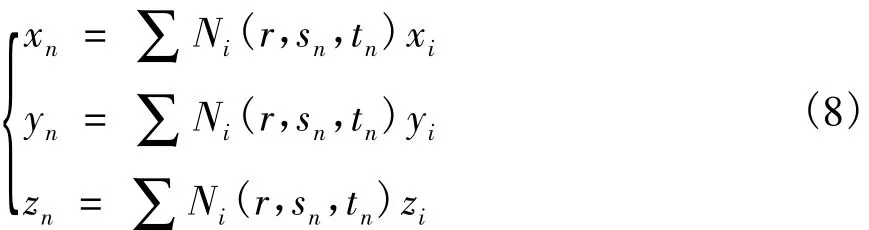
以上所采用的数值计算方法易于在计算机上实现，具有计算速度快，收敛性好等优点。

3 算例

如图4矩形截面简支梁，梁段全长L=6 m，截面高h=0.4 m，宽b=0.2 m，钢筋直径d=0.02 m，BC段和DE段为钢筋弯起段，弯起半径为3 m，钢筋B端和E端到截面底边的距离为0.18 m，CD段钢筋到截面底边的距离为0.04 m。取混凝土弹性模量Ec=2.0×104MPa，泊松比v=0.2钢筋弹性模量Es=2.0×105MPa，在梁的上表面作用有集度为q=500 kN/m2的均布荷载。

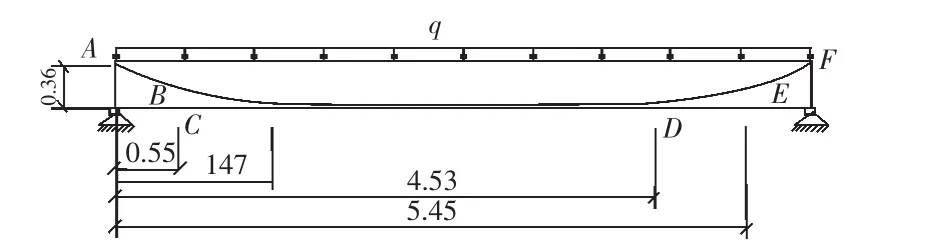
图4 受分布荷载的钢筋混凝土简支梁Fig.4 The reinforced concrete simple beam subject to distributed load

在混凝土结构中加入导线法线形钢筋，并用RCF软件计算钢筋混凝土结构中钢筋的受力状态。考虑钢筋主要以轴向受力为主，钢筋单元采用杆单元模拟［7］。

结构的网格划分按如下方式完成。沿梁的长度方向划分为20个三维8节点等参体元，钢筋网格单元长度设置为0.2 m。全部钢筋单元的节点用软件自动分析找到母单元，并设置全部自由度与母单元位移场一致。

为了充分反应加入交点后筋元与混凝土单元的位移协调关系，图5将未插入交点时筋元与体元面相交处两者位移的差值和插入交点后筋元与体元面相交处两者位移的差值进行比较［8］。

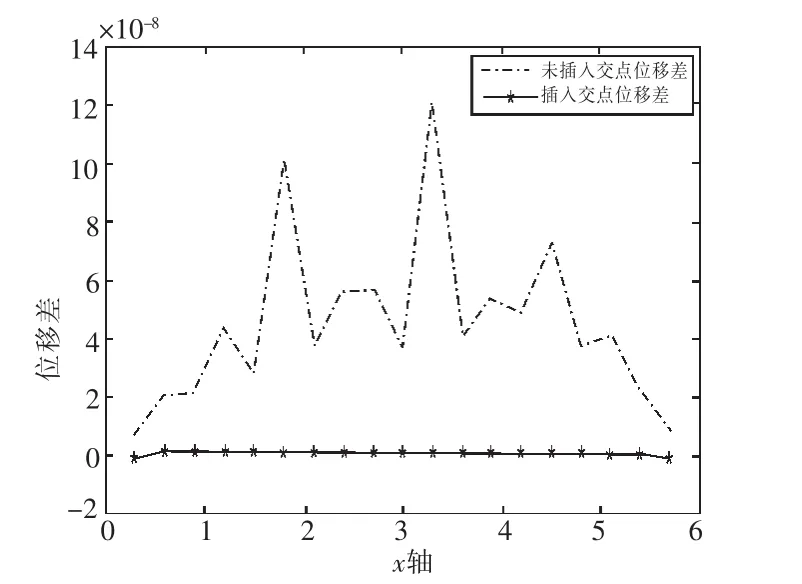
图5 位移差对比Fig.5 Comparison chart of displacement difference

未插入交点位移差代表了未插入交点时筋元与体元面相交处两者位移的差值，插入交点位移差代表了插入交点后筋元与体元面相交处两者位移的差值。由图5可以看出，界面未设置交点时，位移差虽很小，但存在，表明钢筋与混凝土单元之间位移的不协调性。插入交点后，完全消除了两者的位移差，实现了二者的位移协调。

4 结论

通过算例演示了非节点连接方法中筋元与体元在单元交界面处的位移协调性。采用在筋元与体元面相交处插入交点的方法，消除了筋元与体元之间位移的不协调性，可进一步实现加筋结构有限元的精细分析。

［1］王勖成.有限单元法［M］.北京:清华大学出版社，2003.

［2］李青森，杨文兵，杨新华.预应力梁的组合结构分析方法及其有限元实现［J］.华中科技大学学报:城市科学版，2005，22(增刊):84－90.

［3］江见鲸.钢筋混凝土结构非线性有限元分析［M］.西安:陕西科学技术出版社，1994.

［4］王家林.非节点连接有限元理论及其软件实现［D］.重庆:重庆大学，2008.

［5］王家林.钢筋混凝土结构空间有限元分析的体梁组合单元［J］.工程力学，2002，19(6):131 －135.

［6］巫昌海.三维钢筋混凝土非线性有限元及其工程应用研究［D］.南京:河海大学，2000.

［7］El-Mezaini N，Citipitioglu.Finite element analysis of prestressed and reinforced concrete structures［J］.Journal of Structural Engineering，ASCE，1991，117(10):2851－2864.

［8］朱横君.MATLAB语言及实践教程［M］.北京:清华大学出版社，北京交通大学出版社，2005.