内圈大挡边表面粗糙度对圆锥滚子轴承振动值的影响
姜国志,金丽华,李 琴,韩玉连
(烟台西蒙西轴承有限公司,山东 烟台 264006)
轴承的振动与其工作表面粗糙度有直接关系,不同波距的表面粗糙度在轴承振动中通过不同的振动频率表现出来。为了研究内圈大挡边表面粗糙度对圆锥滚子轴承振动值的影响程度,选择大小两个型号轴承进行了试验分析。
1 试验方法
试验采用速度型测振仪(标定合格的BVT-1A)分别测量高、中、低3个频段的振动值,测量装置如图1所示。轴承内圈端面紧靠芯轴轴肩,并与芯轴一起以1 800 r/min的转速旋转,外圈静止,对外圈施加轴向载荷,传感器设定在外圈的外圆表面上且对应于受载外圈滚道与滚子接触中部的平面上。选取外圈外圆柱表面圆周方向大致等距的3点进行测试,其低、中、高3个频段的振动速度的算术平均值即为该轴承在对应频段的振动(速度)值。32208,30202轴承测量时施加的轴向载荷分别为110,60 N。

图1 振动测量示意图
试验时,用泰勒仪测量内圈大挡边表面粗糙度并逐一编号记录,清洗合格后的零件合套,使用速度型测振仪测量振动值并对应编号记录。将测量后的内组件拆套,采用数控挡边超精机对挡边进行超精,测量挡边表面粗糙度并对应编号记录,重新组装合套,其他条件不变,测量振动值并对应编号记录。
2 试验结果与分析
试验数据见表1和表2。从振动值的平均值看,其低、中、高频段变化都很小,为了排除零件间质量差异/测量误差等系统误差的影响,决定采用单因素方差分析法对试验数据进行显著性统计分析(取α=0.05)[1]。

表1 32208轴承挡边超精前、后的振动值及表面粗糙度对比

表2 30202轴承挡边超精前、后的振动值及表面粗糙度对比
设因素A有m个水平A1,A2,…,Am,在水平Aj(j=1,2,…,m)下,进行nj(nj≥2)次独立试验,得到表3结果。
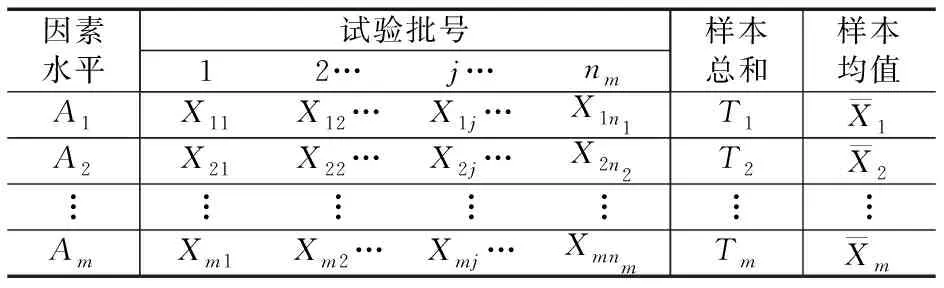
表3 因素A试验表
表4为单因素方差分析表,其中:SS为偏差平方和;df为自由度;MS为均方;F为统计量的计算值;Fα为统计量的“F检验”临界值,可通过查F分布表获得;α为显著性水平,α=0.05的情况下为显著;H0为不同方案间没有显著性差异的假设;SSE为误差平方和(组内偏差平方和);SSA为效应平方和(组间偏差平方和);SST为总变差(总偏差平方和)。

表4 单因素方差分析表
表5为采用单因素方差分析法对32208,30202轴承挡边超精前、后表面粗糙度及振动值的低、中、高频带分析结果,其中:角标1,2分别表示32208,30202轴承;F0.05为“F检验”在显著性水平α=0.05的临界值。
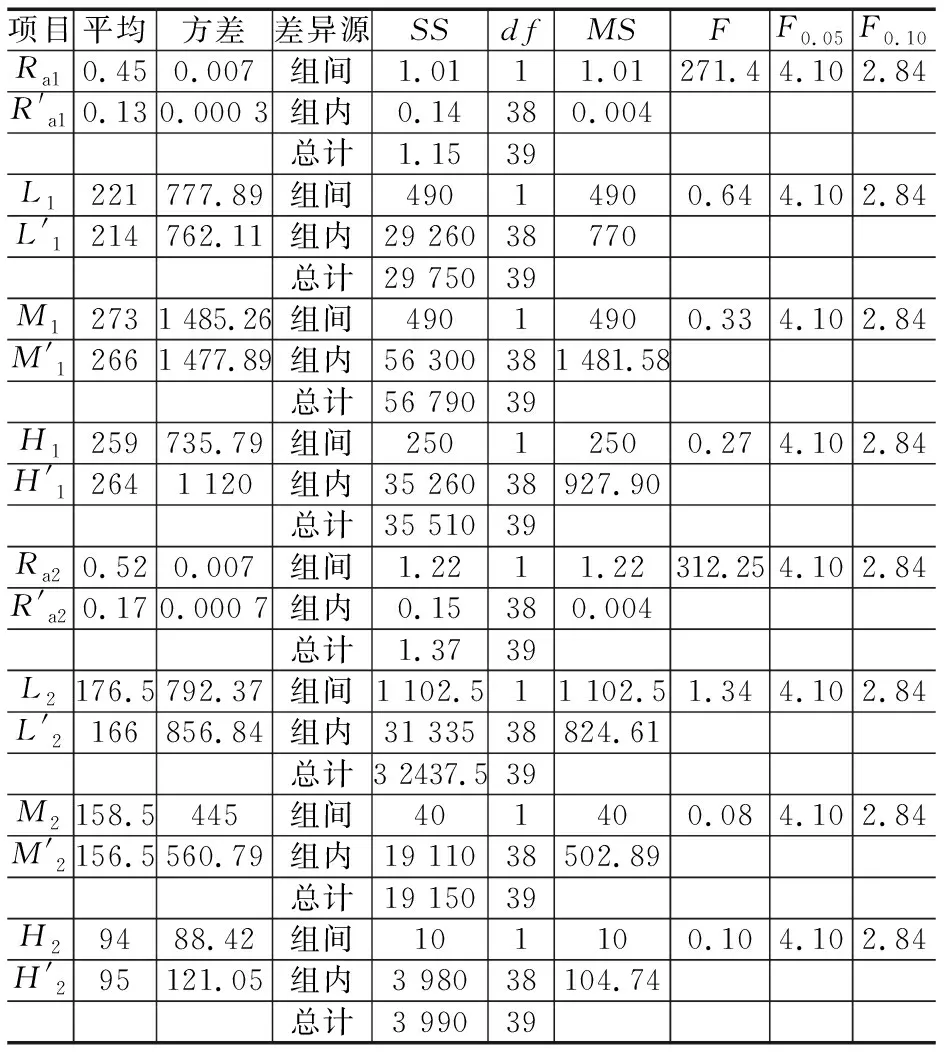
表5 32208,30202轴承挡边超精前、后表面粗糙度及振动值分析结果(α=0.05)
由于F>F0.05=4.10,故在水平0.05下拒绝H0,认为挡边超精前、后表面粗糙度有明显差异,得到很大改善。
由于F 对32208,30202,LM102949/10,30310,M802048/10和LM11949/10共6个型号圆锥滚子轴承进行了相同试验,分析后得到的结论相同。 内圈大挡边表面粗糙度对圆锥滚子轴承振动影响很微小,故采取改善挡边表面粗糙度的措施来降低轴承振动的意义不大。3 结束语

