基于反共振原理的双频载荷作用下轴承保护环的设计

范欢迎

(南京理工大学 泰州科技学院，江苏 泰州 225300)

滚动轴承是大型冶金和筛分洗选等设备中最易损坏的零件之一。过去滚动轴承按刚性支承处理的设计思路过分简化了转子-轴承系统的动力学问题，往往不能得到足够准确的解答。转子-轴承系统研究工作大多基于线性转子动力学理论[1-3]，对转子-轴承系统的稳定性、幅频特性及响应函数进行研究。近年来，随着计算机技术和非线性动力学理论的发展，对转子-轴承系统的非线性研究也在进行，由于接触非线性的存在，轴承支承的转子系统是典型的非线性多自由度动力系统。但是现有的非线性动力学理论和方法在解决Gauss动力系统方面还存在困难，而且，现有的非线性理论只是单独考虑转子-轴承系统，并没有根据各个设备的特点建立起整个系统动力学模型，因此在用非线性理论对一些旋转机械特别是大型筛选机械的轴承系统分析时仍然不能得到很精确的解。

1 双频载荷作用下轴承保护环刚度计算

在筛分加工中，振动筛是一种重要设备，其由转轴、偏心块、轴承以及筛箱和弹簧组成的动力学系统可简化为2自由度动力学模型[4]，如图1所示。

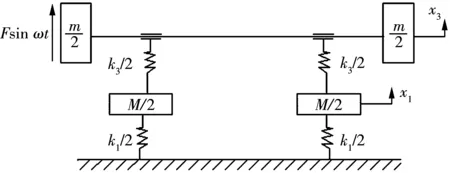
M—筛箱质量；m—偏心块质量；k1—支承弹簧刚度；k3—轴承刚度；F—偏心块产生的最大激振力；ω—偏心块角频率；t—时间；x1—筛箱振幅；x3—偏心块振幅图1 振动筛弹性振动力学模型

振动筛在工作过程中，偏心块引起的很大激振力将造成轴承的弹性振动，轴承在高转速、大激振力的作用下很容易发生大的弹性变形，从而引起轴承较大的磨损以及发热，造成轴承过早损坏。

在实际生产和生活中的机器或结构物均可看作一个振动系统，若在激振力作用下做强迫振动，当激振力的频率与系统固有频率相等时，往往发生较为剧烈的共振运动。一般来说这种情况会对机器造成不利影响。由反共振原理[5-6]可知，若在机器上附加一个质量弹簧系统，构成一个多自由度的振动系统，选择适当的弹性系数，就会使系统的振动变为零，从而达到保护系统的目的。下面就利用此原理设计双频载荷(即振动筛的激振源由两个偏心块提供，当两个偏心块的转速不同时，振动筛会在两个不同频率的激振力下运行)作用下的轴承系统。

由于反共振原理要求在系统中增加一个自由度，因此设计一种弹性支承保护环施加在轴承的外圈上(即轴承保护环与轴承外圈采用基轴制过盈配合，由轴承保护环的弹性支承体的根部和轴承外圈提供压紧力)，其形状如图2所示。这样双频载荷作用下的振动筛弹性振动的动力学模型就变成了3自由度振动系统，其力学模型便简化为如图3所示。

图2 轴承保护环的结构

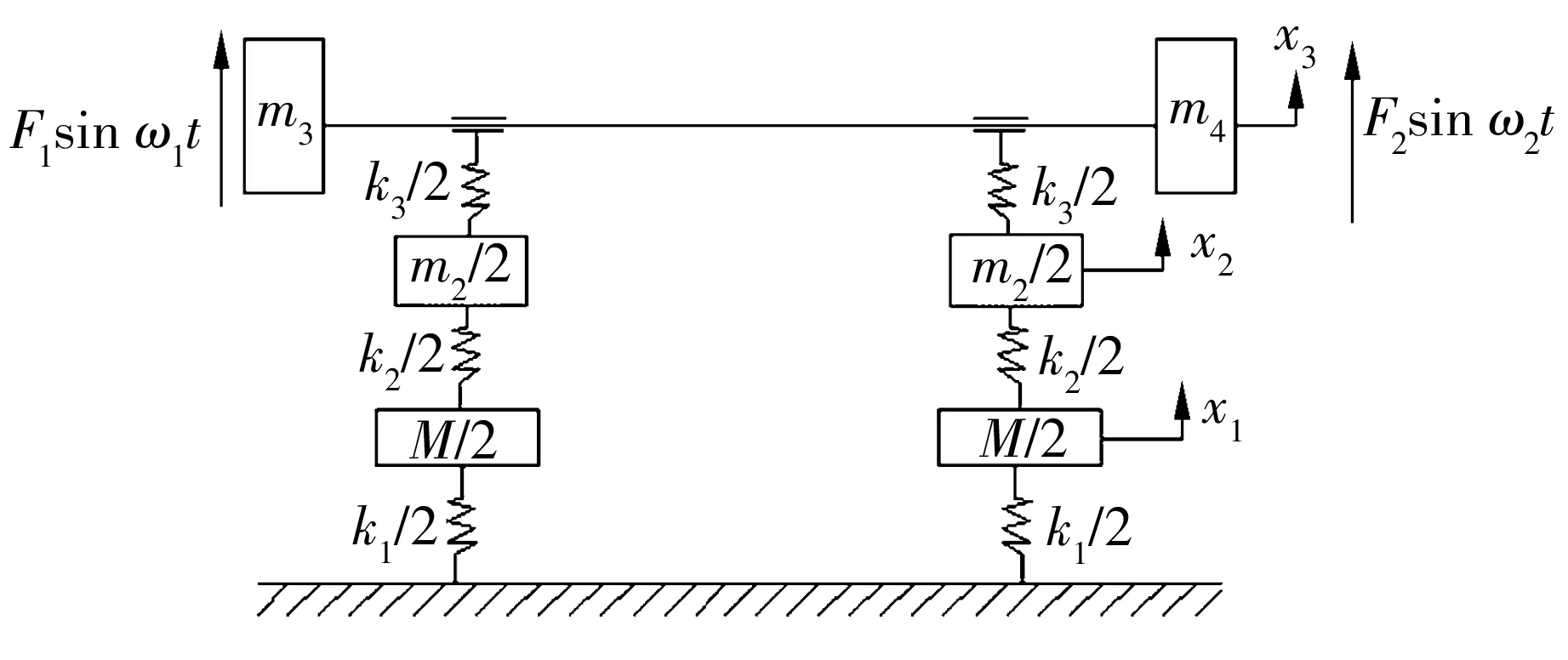
m2—轴承和保护环质量；m3—偏心块1的质量；m4—偏心块2的质量；k2—轴承保护环刚度； F1—偏心块1产生的最大激振力；F2—偏心块2产生的最大激振力；ω1—偏心块1的角频率；ω2—偏心块2的角频率；x2—轴承的振幅图3 双频载荷作用下弹性支承振动筛力学模型

在偏心质量块1产生的激振力作用下，整个系统的弹性振动力学模型为：

(1)

在偏心质量块1产生的激振力作用下，轴承的振幅为：

x4=D4/D

(2)

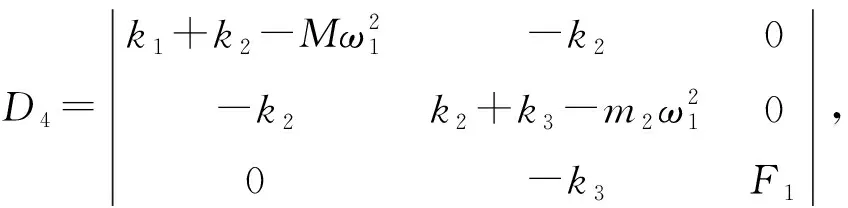
(3)

同理可知，在偏心质量块2产生的激振力作用下，整个系统的弹性振动力学模型为：

(4)

在偏心质量块2产生的激振力作用下，轴承的振幅为：

x5=D5/D′。

式中：

(5)

将振幅x4和x5相加即可得到轴承产生的总振幅：

x=x4+x5

(6)

当x在极小值点时，总振幅x的导数应为零，即x′=0，故：

(7)

2 有无轴承保护环时轴承振幅的比较

6305轴承的径向刚度k3为4.5×107N/m，支承弹簧刚度k1为1×105N/m，筛箱质量为200 kg，轴承质量为0.23 kg，轴承保护环的质量大约为1 kg。偏心块1的质量为20 kg，偏心距为0.05 m，转子转速为2 400 r/min，转子角加速度为ω1=(2 400/60)×2π=80π；偏心块2的质量为20 kg，偏心距为0.05 m，转子转速为1 800 r/min，转子角加速度ω2=(1 800/60)×2π=60π。

由(7)式计算可知弹性支承体等效刚度为：

k2=1.9×107N/m。

没有加入轴承保护环时，图1所示的振动筛动力学模型可表示为：

(8)

系统振动时，轴承的振幅为：

x2=D3/D″

(9)

式中：

没有加入轴承保护环时，根据刚度计算公式可得到偏心块1作用下轴承的振幅为：

在偏心块2作用下，轴承的振幅为：

总的振幅为：

在加入了刚度为1.9×107N/m的轴承保护环后，在偏心块1作用下，轴承的振幅为：

x4=2.3 mm。

在偏心块2作用下，轴承的振幅为:

x5=0.3 mm。

总的振幅为:

x=x4+x5=2.6 mm。

由此可见，在双频载荷作用下，轴承系统加入了轴承保护环以后，振幅由7.3 mm变为2.6 mm，大大减小了轴承的振幅，从而达到保护轴承的目的。

3 试验研究

在实验室柔性转子动平衡系统上进行弹性振动研究，试验装置如图4所示，其是由刚性转子、偏心圆盘、轴承组成的Joffcott转子-轴承系统。测试装置包括两个非接触式涡流传感器和一个信号处理器。由于涡流传感器固定在机架上，所以示波器上显示的是在轴承弹性振动情况下的轴承轨迹，轴承在没有弹性保护环的情况下测得的转轴轨迹如图5所示，在加入了优化设计后的弹性保护环以后测得的转轴轨迹如图6所示。由此可以看出，在没有加入保护环以前，轴承振动轨迹比较复杂，叠加有高次谐波信号，在加入了保护环以后，高次谐波信号得到了很好的抑制，说明此时轴承振动的振幅相对较小，起到了保护轴承的目的。

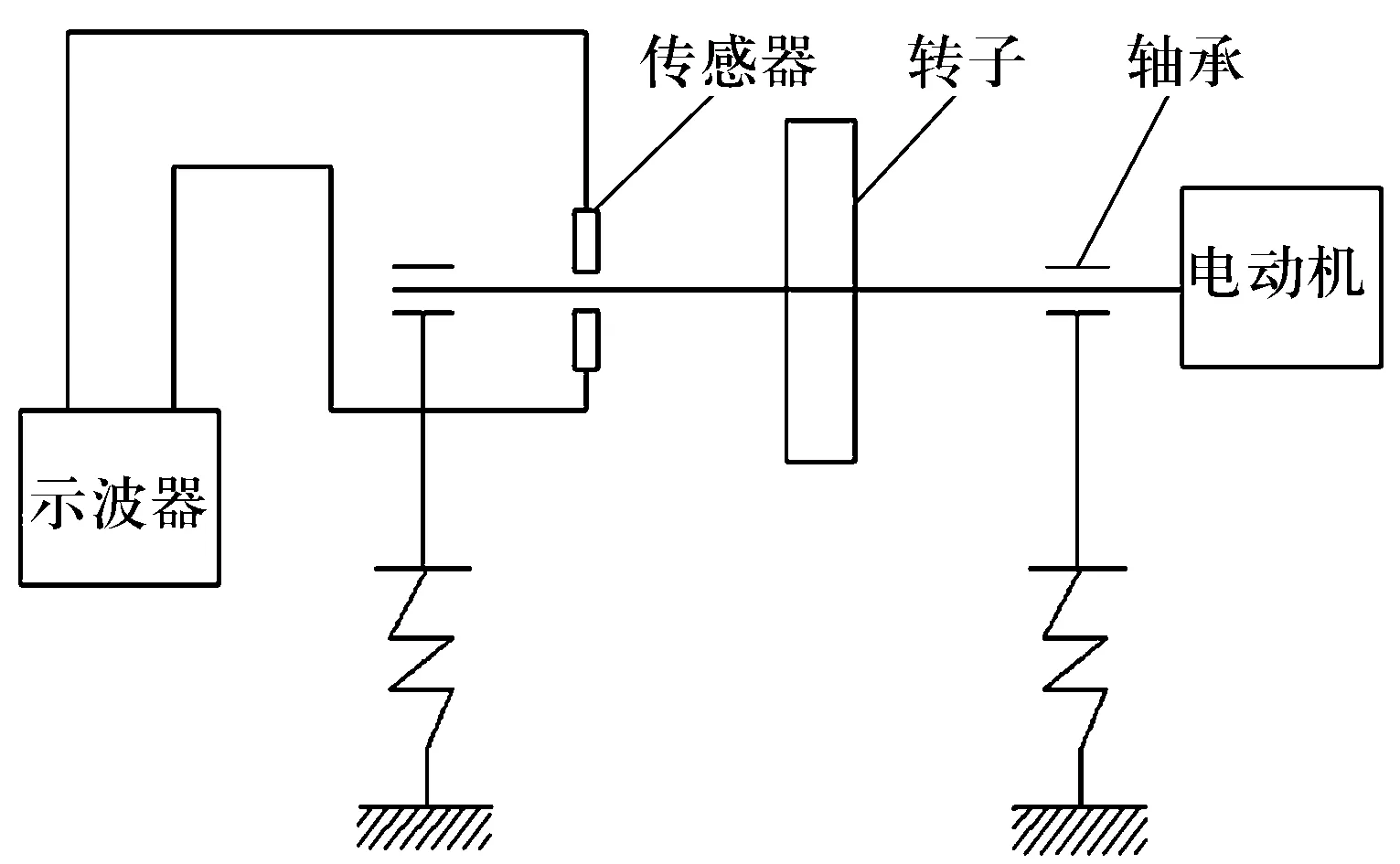
图4 试验装置

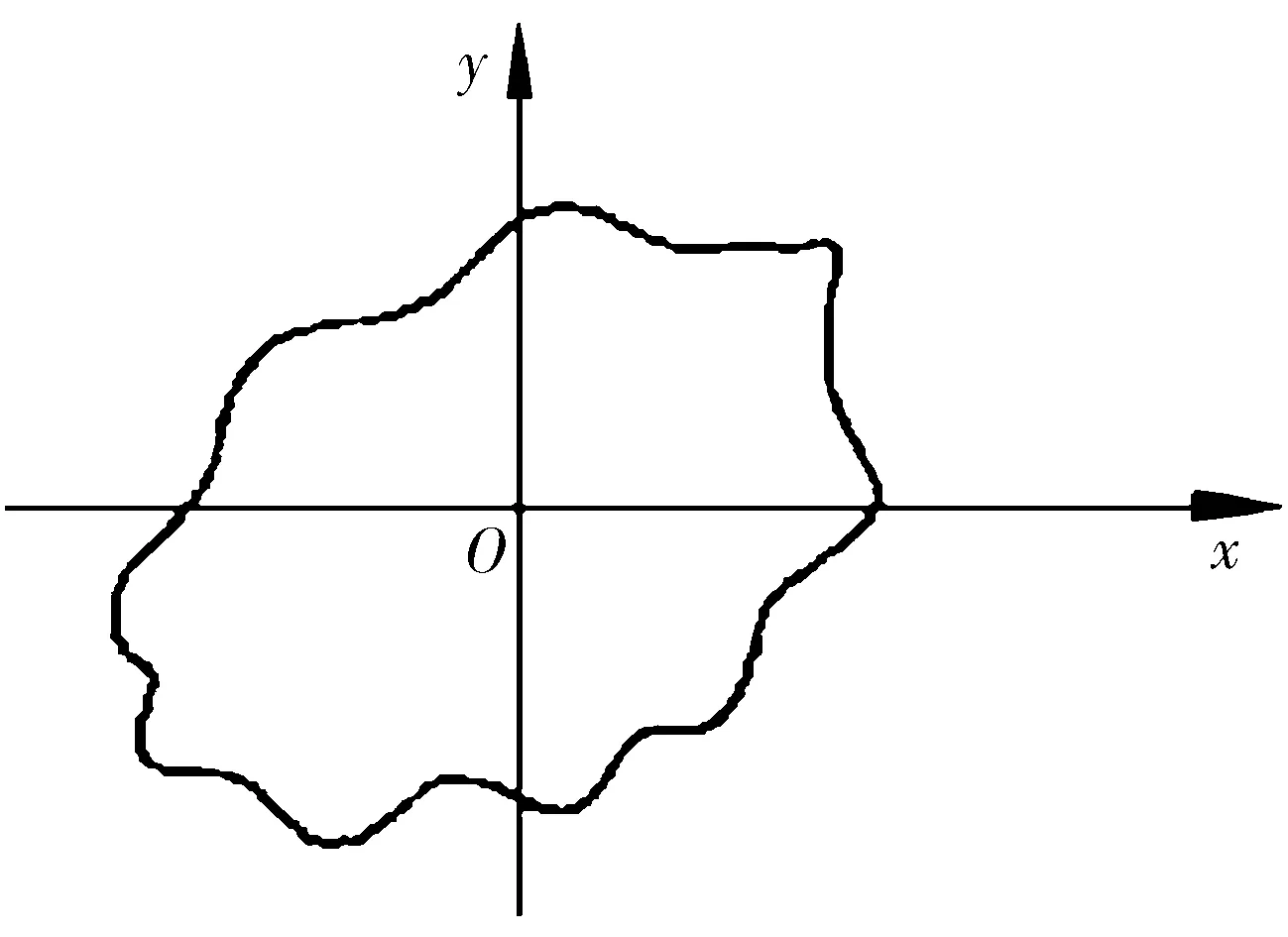
图5 无弹性保护环时转轴轨迹

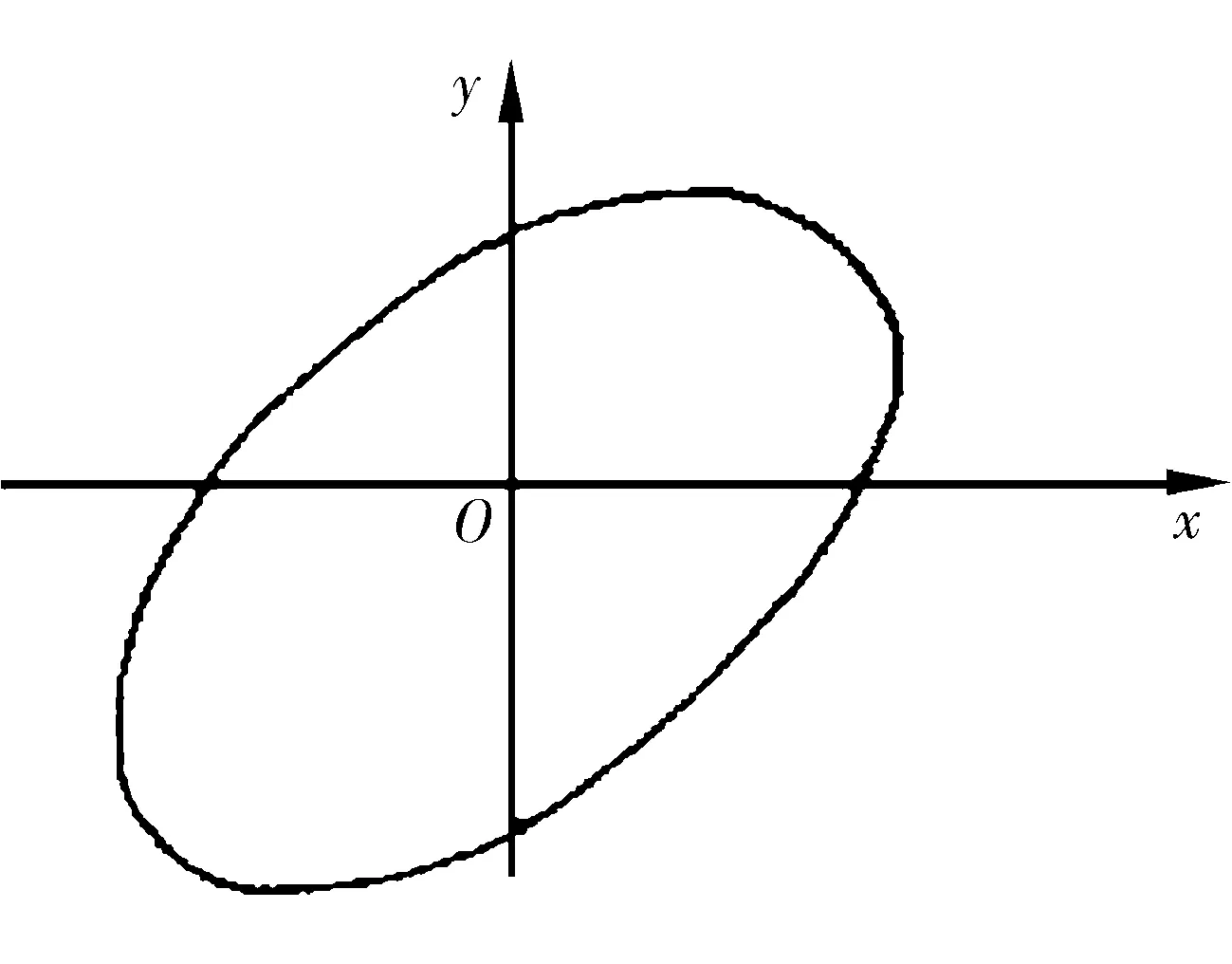
图6 有弹性保护环时转轴轨迹

4 结束语

振动筛的由转轴、偏心块、轴承以及筛箱和弹簧组成的动力学系统可以简化为2自由度动力学模型。由反共振原理可知，若在机器上附加一个质量弹簧系统，构成一个多自由度的振动系统，选择适当的弹性系数，就会使系统的振动变为零，从而达到保护系统的目的。基于此理论,设计了一种弹性支承保护环安装在轴承的外圈上，并推导了双频载荷下轴承保护环的等效刚度公式，最后将有、无轴承保护环时的轴承振幅进行了对比，结果表明，加入轴承保护环后的轴承振幅大大降低，从而达到了保护轴承的目的。试验证明，在双频载荷作用下，加入轴承保护环能很好地达到保护轴承的目的。