基于脑电特征的多模式想象动作识别

万柏坤，刘延刚，明 东，孙长城，綦宏志，张广举，程龙龙

(天津大学精密仪器与光电子工程学院，天津 300072)

脑-机接口(brain-computer interface，BCI)是运用工程技术手段在人脑和计算机或者其他电子设备之间建立的直接信息交流和控制通道[1]．BCI可以为思维正常但运动功能残缺的病人提供辅助运动功能，也可以大大扩展人与外界进行交流和对外界进行控制的能力[2]．

1 BCI系统

典型的 BCI系统如图 1所示，其技术研究的核心是从电极所检测到的脑电信号中识别出人脑思维操作的意图，提取能反映操作者主观动作意图的特征参数并通过适当的算法把它转换为控制外部设备的命令[3-4]．

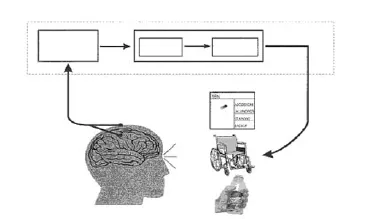
图1 典型的BCI系统结构示意Fig1 Typical structure of BCI system

现代神经电生理学的研究表明，人体实际的肢体动作或者仅是大脑的想象动作均可引起诱发脑电信号内某些特征频段成分(如 alpha波、beta波等)的功率谱强弱变化，其中功率谱比率下降的现象称为事件相关去同步化(event related desynchronization，ERD)现象，而功率谱比率上升称为事件相关同步化(event related synchronization，ERS)现象[5-6]．

不同肢体部位动作诱发的ERD/ERS现象在发生频段上具有明显的差异，如手部动作诱发的 ERD现象较为显著，多发生于 10～12 Hz及 20～24 Hz频段；而舌部动作的ERS现象较为显著，多发生在10～11 Hz，足部动作则为发生在 7～8 Hz及 20～24 Hz频段的 ERD现象．另外，不同肢体部位的动作诱发的 ERD/ERS现象还具有不同的皮层区域分布，由于人体大脑皮层感觉运动区神经冲动的传导方式具有左右交叉、上下颠倒的特征，因此皮层区域分布表现出对侧占优的特点．如当进行左手的想象动作时，右侧皮层初级感觉运动区表现出更强的ERD现象[7]．

ERD/ERS现象的发生频段和分布区域的特异性使得其可以用来作为脑-机接口中自主运动意识信息的转化工具，如将不同部位的肢体想象动作对应于不同的控制指令，则通过对脑电信号中 ERD/ERS现象的发生频段和分布区域进行分析，即可提取出想象动作对应的肢体部位，从而解析出使用者所要传达的控制指令．因此，脑-机接口研究中将肢体想象动作诱发的 ERD/ERS作为一种经典范式，传统的使用方式是采取左、右手想象动作的双模式机制，这主要是由于左手和右手两个部位的皮层特征区域距离较远、脑电特征较为稳定，从而有利于识别．然而以识别左、右手想象动作诱发脑电特征的方式传递自主信息时，每个想象动作任务仅可输出 1,b信息(如识别出左手动作输出0，识别出右手动作则输出1，相当于输出1位数字信号)．显然这种模式下的脑-机接口信息传输效率比较低，不利于 BCI系统复杂控制功能的实现．因此逐步扩展动作模式的范畴，采用更多的动作模式以提高 BCI系统的性能已成为目前的研究共识．笔者对包括左手、右手、足部和舌头 4个想象动作模式进行研究，探讨多模式想象动作诱发信号的特征提取和识别方法，理论上4种动作模式可以提供2倍的信息传输速率．

2 实验数据

采用的实验数据来源于国际 BCI CompetitionⅢ的公开数据库[8]，数据库中的脑电信号数据所采用的动作任务是由左手、右手、足部和舌头 4个部位的想象动作组成的．每个任务时间长度为 8 s，其中，第1秒到第 2秒为任务的准备期，此期间内要求受试者保持安静状态．第 3秒为任务的提示期，期间计算机屏幕出现一个“＋”的符号标志以提示受试者下一秒钟将开始执行想象动作任务．第 4秒到第 7秒的时间为想象任务的动作期，此期间符号“＋”在计算机屏幕上消失而代之以出现一个“→”、“←”、“↓”或者“↑”的符号标志，该标志在该期间内一直保持显示在计算机屏幕上，当该标志出现后，即要求受试者按照箭头方向所示执行左手、右手、足部或者舌头的想象动作任务．第8秒为任务的恢复期，提示符号标志消失，计算机屏幕恢复灰黑色背景，受试者停止想象动作恢复平静状态．实验中所采集的任务同步脑电数据为60导联，导联的位置如图2所示[8]．

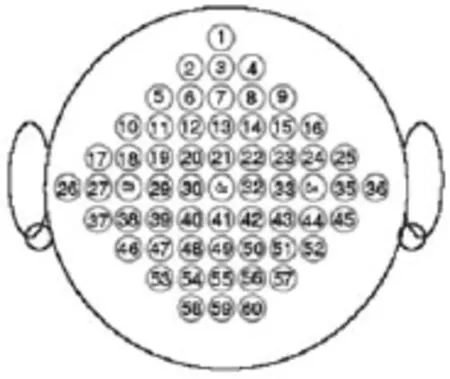
图2 多模式想象动作的导联位置示意Fig.2 Position of EEG electrodes of multi-pattern motor imagery

3 时频分析与ERD/ERS

时频分析[9]可作为想象动作诱发脑电ERD/ ERS信号的处理基础，是由于想象动作引起的 ERD/ERS现象有着特定的发生频段和相对于诱发刺激固定的时间延迟，因此采用基于短时傅里叶变换的时频分析方法对事件发生前后的功率谱密度变化及分布特点进行分析．短时傅里叶变换(short time Fourier transform，STFT)是目前最常用的时频分析方法之一，其做法是先使用一个有限宽度的观察窗 W(t)对信号x(t)进行观察，然后对加窗后的信号进行傅里叶变换

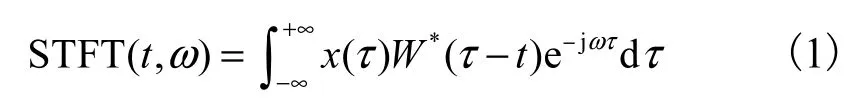
式中：ω是角频率；*( )Wtτ−是()Wtτ−的复共轭函数．逐步移动观察窗对整个肢体想象动作任务刺激下的脑电信号 x(t)进行观察，可以得到单次任务的二维时频图谱(如图 3所示)．由于诱发脑电信号的信噪比不高，单次任务脑电信号易出现偏差或者噪声太大，因此，采用多次任务叠加平均的方法来增强信噪比．

经处理，得到各动作模式下的平均二维时频图谱，图 3(a)、3(c)和图 4(c)、4(a)所示分别为左手、右手、足部、舌部4个肢体想象动作中特征最显著导联处的时频图谱．横轴表示时间，纵轴表示频率，伪彩色则代表经过叠加平均后的功率谱密度(单位为 dB)．可以看出，左、右手和足部动作的ERD现象显著，而舌头的想象动作则诱发出较为明显的ERS现象．

图3 左、右手想象动作特征导联处的二维时频图谱和空间分布地形Fig.3 Two-dimensional time-frequency atlases and spatial distribution map of feature channels of left and right hand motor imagery

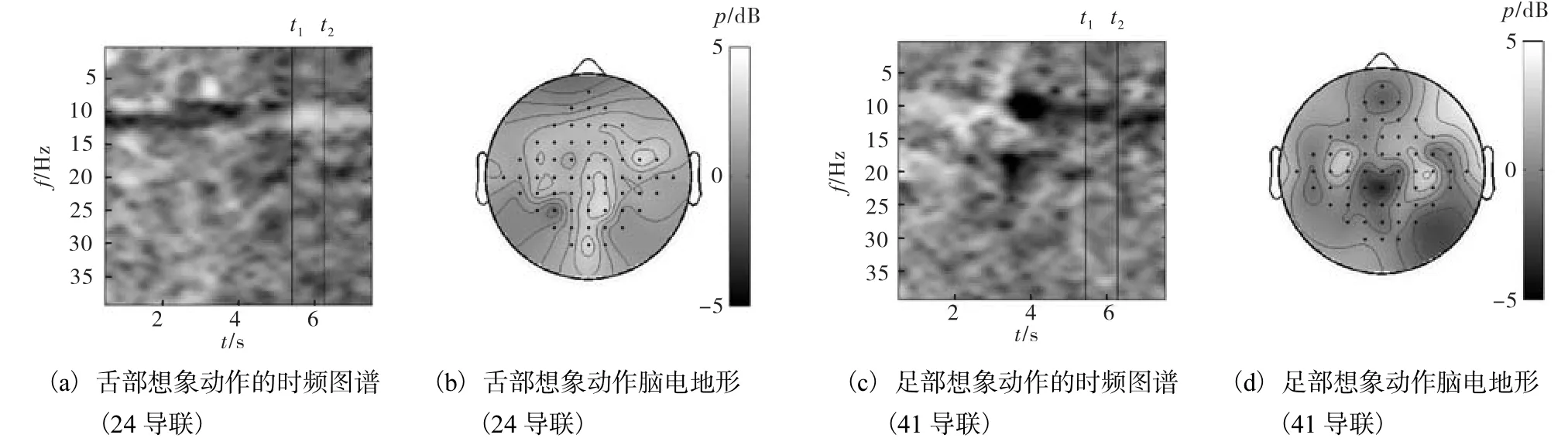
图4 舌部和足部想象动作特征导联处的二维时频图谱和空间分布地形Fig.4 Two-dimensional time-frequency atlases and spatial distribution map of feature channels of tongue and foot motor imagery

时频图谱中标示的 t1、t2为 ERD/ERS特异性最强时段，此时段内的平均功率谱密度在头皮上的空间分布如图 3(b)、3(d)、4(b)、4(d)所示，可见 4 种模式想象动作的空间分布均具有较强的特异性，其中左、右手想象动作的ERD现象分别在34导联和28导联处最显著(为左右交叉对应)，足部想象动作诱发的ERD在41导联处最显著，而舌头部位的ERS现象在24导联处最强．

时频分析的结果表明，想象左手、右手、足部和舌头动作可以引起特异性较强的频谱变化，并伴随有显著的空间分布，根据这些信息提取出特征参数即可用于不同动作模式的分类识别．但由于不同动作模式诱发的ERD/ERS现象的特征频段和响应时段有所不同，因此需要采用可分性分析进一步提取出有利于识别的特征频谱参数．

4 Fisher可分性分析与特征提取

信号的可分性分析是想象动作特征电位提取的关键部分，可分性分析作为特征提取的方法，主要用来评价特征参数在不同类别样本中的分布是否具有明显的差异，一般差异度越大的参数越适于作为样本分类的特征值．采用 Fisher可分性分析进行频谱特征的提取，其基本描述[10]为

式中：m1与 m2分别为两类特征的均值；σ12与 σ22分别为两类特征的方差．Fisher分析的评价函数J实际上是特征值的类间离散度与类内离散度的比值，J值越大则可分性越高，若两类特征的均值相等，则 J为0，两类特征线性不可分．

采用 Fisher分析的方法对二维时频网格上两类动作模式的功率谱密度特征进行处理，选择J值较大且集中的频段和时段(特征频段和特征时段)进行分类特征的构造．下面以 34导联处想象左手动作与其他动作之间的 Fisher分析为例来说明特征频段和特征时段的提取方法．

首先，对每一次实验的数据进行二维时频处理，将左手动作数据作为样本 1，以其他动作的数据作为样本 2，然后在二维时频网格上对每一节点处的两个样本集计算其 Fisher系数(J值)，这样可得到 Fisher系数的二维时频分布图(如图 5(a)所示)．对动作期(3～7 s)内的 J值按照时间轴进行平均，可得到随频率变化的 J值曲线(如图 5(b)所示)，该曲线上的两个波峰表示左手想象动作与其他想象动作模式之间存在两个具有特异性差别的频段，采用阈值提取的方法提取出的即为特征频段．对特征频段F1和F2中的J值按照频率轴进行平均，分别得到特征频段内随时间变化的 J值曲线(如图 5(c)、5(d)所示)．然后，在这两条曲线上分别提取特征时段

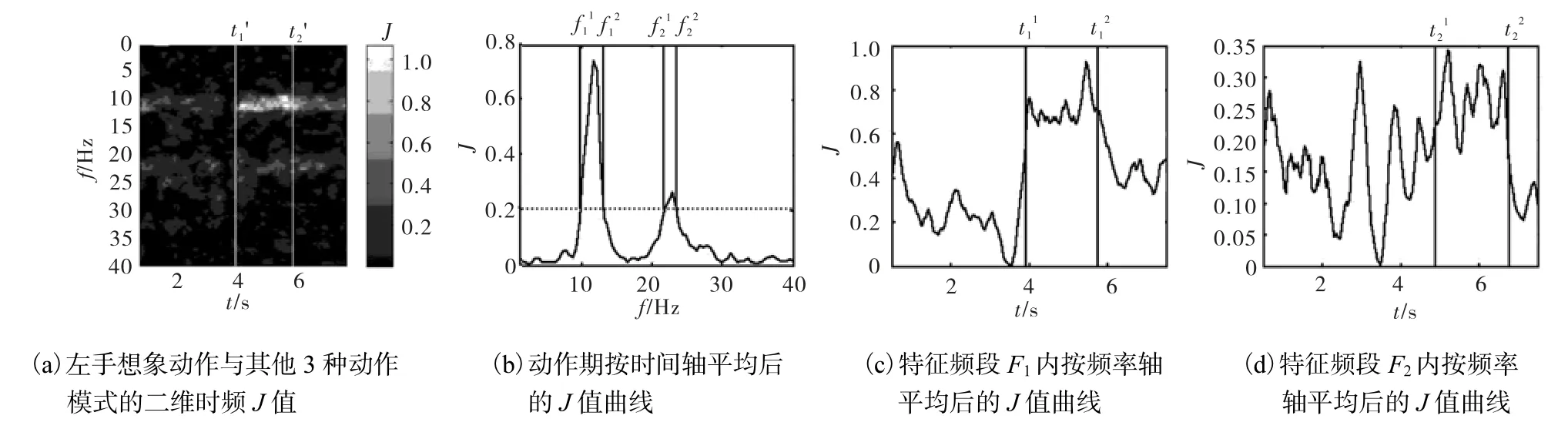
图5 左手想象动作经Fisher分析提取特征频段和特征时段的示意(34导联处)Fig.5 Diagram of extraction of feature frequency bands and time periods of left hand motor imagery by Fisher analysis(at channel 34)

各动作模式的分类特征是以特征频段和特征时段内的功率谱密度均值来构造的，这样得到的特征具有较高的可分性和稳定性．例如，在想象左手动作时，在频段F1和时段 T1上 34导联处的J值为0.828 6，在34导联附近的左手模式特征区域内的所有导联的平均J值为0.473 3，而在剩余的所有导联上的平均J值仅有 0.044 8，显然，左手模式与其他模式之间具有良好的可分性，提取这个区域的导联作为左手模式的特征导联．同样，对其他每种动作模式也提取可分性最好的数个导联，用于构造各模式的特征向量，按照特征的J值大小共提取出4种动作模式下的27个特征值，并按照J值由大到小对每种模式的所有特征进行排序，由于不同特征组合方式会导致不同的识别效果，笔者尝试了3种特征组合方式(如表1所示)进行分类识别，每种组合中使用的各模式的特征均从其所有特征中选择J值最大的若干个．组合1与组合2中的特征基本分布在各肢体部位的皮层功能区上，组合3中的特征分布较广，除各对应功能区外，还有部分特征位于其他区域，如额区和枕区．

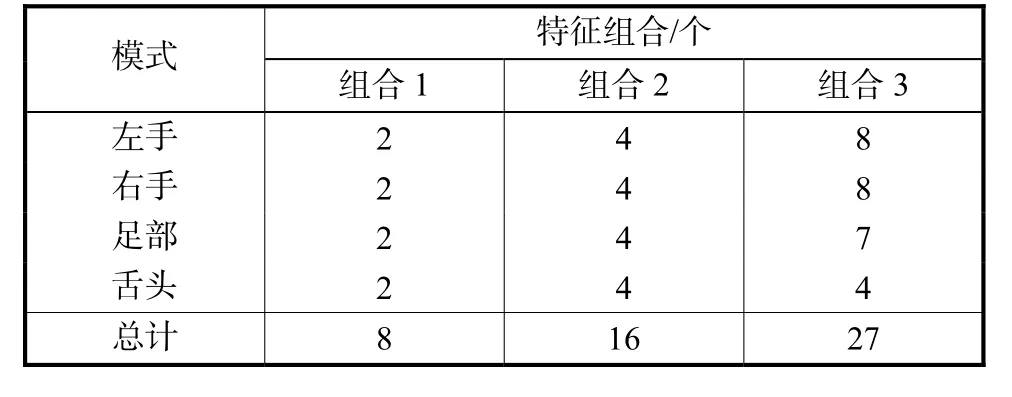
表1 4种模式的3种识别特征组合Tab.l Three kinds of compages of recognition features of four classes

5 基于SVM的分类识别结果

分类识别是脑-机接口系统中重要的信号处理环节，是完成使用者自主意识到控制命令转化的关键步骤．对于基于想象动作的脑-机接口系统而言，模式识别即是通过对脑电信号特征的提取和分类来辨识出其中所携带的自主性动作信息．

脑-机接口的识别环节中，分类器建立过程中可以使用的训练样本数往往比较有限，这种情况下传统的分类识别方法如神经网络等存在识别准确率偏低、分类器泛化能力不强、识别效果不稳定等问题．基于统计学习理论的支持向量机(support vector machine，SVM)方法是近年来在模式识别与机器学习领域中得到广泛认可的分类识别技术，它可以有效地避免经典学习方法中的过学习、维数灾难和局部极小等问题，在小样本条件下仍具有良好的泛化能力．因此，采用SVM 的方法来对提取到的想象动作脑电信号的特征参数进行分类识别[11]．

文中处理的识别问题属于多分类识别(共4种动作模式，也即4个类别)，实践上可采用两种方案进行分类：①单层分类，即同时对4种模式进行识别；②双层分类，第1层分类首先对4种模式按照特征的分布特点分为两类(左手和右手动作模式为一类，足部和舌部动作模式为另一类)，第 2层分类是在第 1层分类的结果上在两类内部继续细分．对这两种方案进行测试并对其结果进行比较分析，将所有单次实验样本分为训练集和测试集，首先使用训练集训练 SVM分类器并进行参数优化，然后使用测试集放入分类器中进行测试得到识别正确率，其结果如表2所示．

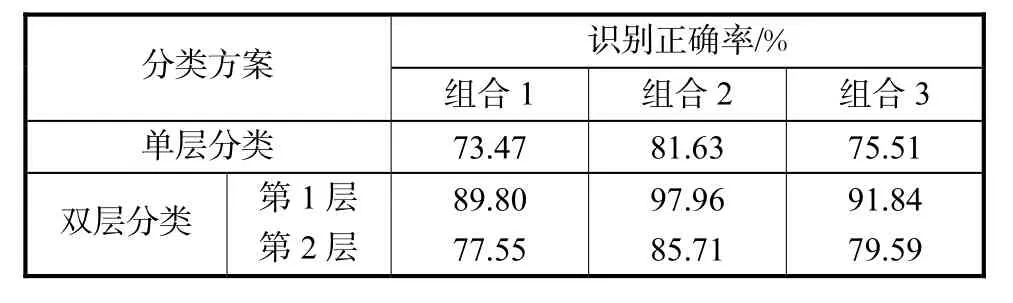
表2 不同特征组合和分类方案下的识别结果Tab.2 Recognition results under different kinds of feature Tab.2 compages and classification schemes

由表2可以看出采用16个特征的特征组合及双层分类方案下识别正确率最高，可达到 85.71%．对于不同的特征组合，组合2的识别正确率高于其他两个组合，单层分类器方案下，组合 2的识别正确率为81.63%，而组合 1和 3的识别正确率分别为 73.47%和 75.51%；双层分类器方案下，组合 2的识别正确率为 85.71%，而组合 1和 3的识别正确率分别为77.55%和 79.59%．相对于组合 1而言组合 2增加的特征是同样位于相应动作模式的大脑皮层功能区域内，而 J值相对较低的部分特征，由于采用了更多的特征信息，分类效果得到了一定的提高．组合 2高于组合3的原因则较为复杂，一方面组合3中的特征分布已不完全位于相应动作模式的大脑皮层功能区域内，这些功能区外的特征往往是由于脑电的空间低通特性所致，本质上属于一种冗余信息，而且对于识别起不到正面作用，另一方面分类器学习时在样本数一定的情况下，特征维度过高时将带来学习机泛化能力的下降，组合3中的特征维度相对于样本数量而言过高，从而降低了分类器的识别效果．不同特征组合的分类对比结果说明，对于多模式想象动作的分类绝不是特征越多越好，过分增加特征维度有可能带来识别效率的下降．

对于不同的分类器方案，各种特征组合方式下双层分类的最终正确率均比单层分类的高了约 4%(比如 16个特征时，单层分类为 81.63%，而双层分类可达 85.71%)，这也说明双层分类能够改善分类效果，其原因可能是由于支持向量机本身所具有的更适合于二分类的特点．

此外，从表2中可以看到双层分类的第1层分类正确率都很高，在 16个特征时可以达到 97.96%，这说明左、右手模式和足部、舌头模式的功能区和特征频段的分布的可分性相当好；同时，左、右手模式的ERD/ERS信号强度也远远高于足部、舌头模式．

6 结 论

(1)采用二维时频分析结合Fisher可分性分析的方法对多模式想象动作的诱发脑电信号进行特征提取，采用支持向量机构造分类器进行识别，研究结果表明，多导时频特征的优化组合可以获得较高的多模式想象动作区分效果，采用双层的分类器构造方案可以提高分类识别的正确率．

(2)将传统的左右手双模式想象动作脑-机交互任务扩展到左手、右手、足部、舌头 4种模式后，识别效果未见明显下降，这为双模式动作任务向多模式动作任务的推广提供了良好的条件，同时也为进一步扩展动作模式奠定了基础．

(3)肢体想象动作的诱发特征区域性较为集中，而左手、右手、足、舌4个肢体部位在大脑皮层初级感觉运动区内的对应主控区域相互间隔较远，因此其产生的特异性诱发脑电信号仍可表现出空间可分性，这是多模式任务识别的基础原因．想象动作模式的扩展可以提高脑-机交互的信息传输效率，但受制于脑电信号较低的空间分辨率，动作模式的扩展必须考虑到诱发特征的空间分布特异性．因此，进一步的动作模式扩展也应当考虑到诱发特征的区域集中性以及与已有模式的皮层功能区间隔．

［1］ Wolpaw J R，Birbaumer N，Heetderks W J，et al. Braincomputer interface technology：A review of the first international meeting[J]. IEEE Trans Rehabil Eng，2000，8(2)：222-225.

［2］ Wolpaw J R，Birbaumer N，McFarland D J，et al. Braincomputer interfaces for communication and control[J].Clinical Neurophysology，2002，113：94-109.

［3］ 万柏坤，高 扬，赵 丽，等. 脑-机接口：大脑对外信息交流的新途径[J]．国外医学生物医学工程分册，2005，28(1)：4-9.Wan Baikun，Gao Yang，Zhao Li，et al. Brain-computer interface：A new channel for information communicate between human brain and environments[J]. Biomedical Engineering Foreign Medical Sciences，2005，28(1)：4-9(in Chinese).

［4］ Vaughan T M. Brain-computer interface technology：A review of the second international meeting[J]. IEEE Trans Neural Syst Rehabil Eng，2003，11(2)：94-109.

［5］ 庄 平．脑电事件相关去同步化和同步化活动与运动相关性作业[J]. 中国临床康复，2004，8(1)：152-154.Zhuang Ping．EEG event-related desynchronization and synchronization activities and movement relate dexercises[J]. Chinese Journal of Clinical Rehabilitation，2004，8(1)：152-154(in Chinese).

［6］ Pfurtscheller G，Lopes da Silva F H．Event-related EEG/MEG synchronization and desychronization：Basic principles[J]. Clinical Neurophysiology，1999，110(11)：1842-1857.

［7］ Neuper C，Müller G R，Kübler A，et al. Clinical application of an EEG-based brain-computer interface：A case study in a patient with severe motor impairment[J].Clinical Neurophysiology，2003，114：399-409.

［8］ Krusienski D J，Wolpaw J R，Millán José del R. The BCI competitionⅢ：Validating aternative approaches to actual BCI problems[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineeing，2006，14(2)：153-158．

［9］ 殷晓中，于盛林. 信号的时频分析理论及应用评述[J].现代电子技术，2006，29(21)：118-120.Yin Xiaozhong，Yu Shenglin．Time-frequency analysis and its application[J]. Modern Electronic Technique，2006，29(21)：118-120(in Chinese).

［10］ 杨 健，杨静宇，叶 晖．Fisher线性兼备分析的理论研究及其应用[J]. 自动化学报，2003，29(4)：481-493.Yang Jian，Yang Jingyu，Ye Hui．Fisher linear analysis of both theoretical research and its applications[J]. Acta Automation Sinica，2003，29(4)：481-493(in Chinese).

［11］ 胡 哲，郑 诚，闵鹏鹏. 支持向量机及其应用研究[J]. 重庆科技学院学报：自然科学版，2008，10(2)：121-124.Hu Zhe，Zheng Cheng，Min Pengpeng．Support vector machine and its applications[J]. Journal of Chongqing University of Science and Technology：Natural Sciences Edition，2008，10(2)：121-124(in Chinese).