基于自适应粒子群算法的光纤光栅传感器优化配置

王 为，林玉池，沈小燕，赵美蓉，宋 乐

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

传感器优化配置是指将一定数量的传感器布置在结构的合适位置上，包括传感器数量的优化和传感器位置的优化两个方面内容．传感器优化配置是结构健康监测和损伤诊断技术的基础．一方面通过优化配置选择合适数目的传感器可以节约经济成本；另一方面配置合适的传感器网络可以提高检测精度，减少由于数据重复造成的误判．目前关于传感器优化配置的研究主要依据结构模态参数建立优化配置准则，结合某种优化算法如遗传算法，得到传感器的优化数量和优化位置[1-3]．这类方法的主要缺点是：结构模态参数是通过对结构有限元分析获得的，受有限元分析时的约束条件、边界参数等设置的影响很大，难获得准确的结构模态参数．

依据优化配置准则求解合适的传感器网络结构是一种典型的组合优化问题．目前常用的解决组合问题的优化方法如非线性规划法、序列法等都容易陷入局部最优解．而近来发展的基于概率的优化方法如模拟退火算法和遗传算法，以及模仿生物运动的群智能算法如蚁群算法、粒子群算法、鱼群算法等全局型优化算法非常适合类似传感器优化配置的组合优化问题．特别是粒子群优化(particle swarm optimization，PSO)算法，需要设置的参数数量少，且无遗传算法的交叉、变异算子，易于实现，得到了广泛的应用．

光纤光栅(fiber bragg grating，FBG)传感器是波长型传感器，在各类结构健康检测中大量使用，研究其优化配置对提高解调系统效率和经济性具有重要意义．

1 传感器优化配置准则

FBG传感器(以下简称“传感器”)用于结构健康监测，一般是通过检测振动或波动信号获得结构状态参数．考虑到波动信号传输中的扩散、散射及被介质吸收等损耗、噪声干扰及传感器与检测仪器精度等因素限制，传感器的检测信号范围如图 1所示．在半径为 R1的圆周范围内各种因素限制较小，此时传感器能完全有效地检测到信号．依据概率理论，可认为传感器能完全覆盖此范围内信号源发出的信号，即覆盖率为 1；当信号源位于半径为 R2的圆周范围以外时，信号损耗及噪声干扰等因素使传感器已无法有效地检测到信号，即覆盖率为 0；当信号源位于两圆周范围之间时，传感器的覆盖率服从一定的概率分布．考虑到波动信号指数衰减规律及噪声等因素，为简化计算，设概率分布与信号源和传感器的距离呈二次函数关系，即

图1 FBG波动信号检测范围示意Fig.1 Detection range of FBG for variation signal

式中：(x，y)是信号源位置；(x0，y0)是传感器位置；D表示信号源与传感器的距离(用矩阵乘法表示)，即

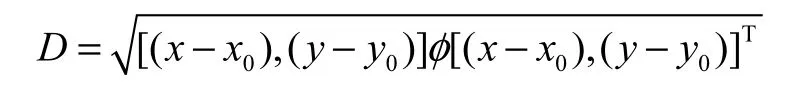
其中φ表示波动信号传播过程中的各向异性的特征[4]，如当 φ = [ 1,0；1,0 ] 时，信号 x、y方向传播特性相同；当 φ = [ 1,0；1,4 ] 时，信号 y方向传播损耗是 x方向的2倍．

设结构上共布置了 N个传感器，该传感器网络对某信号源的覆盖率为

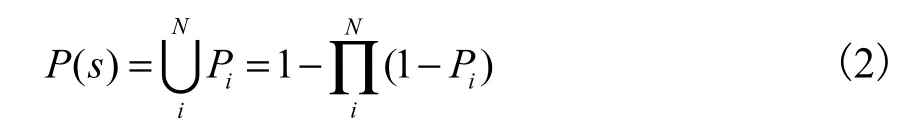
即各传感器覆盖率的联合概率．此时，传感器优化配置效果可用传感器网络对结构上所有信号源的覆盖率最大化来评价．

若被监测结构共有 M 个信号源，则传感器优化配置应使

最小化，此即为传感器优化配置准则．

2 自适应粒子群优化算法原理

称式(3)为优化算法的适应值函数，其最小化的求解是典型的组合优化问题．粒子群优化算法是模拟鸟群的捕食行为[5-，6]而发展起来的一种组合优化问题智能型解决方法．由于它具有所需设置参数少、无交叉、变异算法等特点，得到了广泛应用．

设在m维搜索域中有n个粒子组成粒子群．xi、vi分别为粒子 i的位置向量和速度向量，i＝1，2，…，n；是粒子i当前已搜索到的最优适应值的位置向量；是粒子群当前搜索到的最优适应值的位置向量．PSO算法的更新算法[7]表示粒子群从第t代搜索至第t＋1代的算法过程，即

式中：w为惯性权重；1c、2c均为加速度常数，分别表示将每个粒子推向p和g的权重；1r、2r均为 [0，1]间的随机数．

惯性权重w有平衡算法全局和局部搜索的功能，较大时有利于全局搜索，防止算法“早熟”；较小时有利于局部搜索，能得到更为精确的最优解．因此对w的调节是 PSO算法的一个重要改进方向，如 Shi等[7]提出的随搜索代数线性减小w的方法，将w从0.9线性减小到 0.4，并取得了较好的实验结果．但是线性调整w的方法使其保持较大值和较小值的时间均很短，难以发挥平衡全局和局部搜索的能力；且线性调整方法不能反映搜索过程中粒子群状态．笔者通过分析迭代过程中各粒子当前适应值与粒子群当前最优适应值的分散关系自适应调整惯性权重w，即

式中：w( t + 1 )表示粒子群从第 t代搜索至第 t＋1代的惯性权重；fitness(xi( t))表示第t代第i个粒子的适应值；fitness(g)表示粒子群当前最优适应值；w0为常数．在搜索初期，由于粒子群的随机性，各粒子适应值与当前最优适应值距离较大、比较分散，从而惯性权重较大便于全局搜索；随着搜索进行，各粒子逐渐收敛于最优适应值，惯性权重减小，利于得到精确的最优解．

3 实验与仿真

3.1 FBG波动信号检测实验

为了验证FBG传感器对波动信号的检测范围特点，搭建了如图2所示的实验系统．

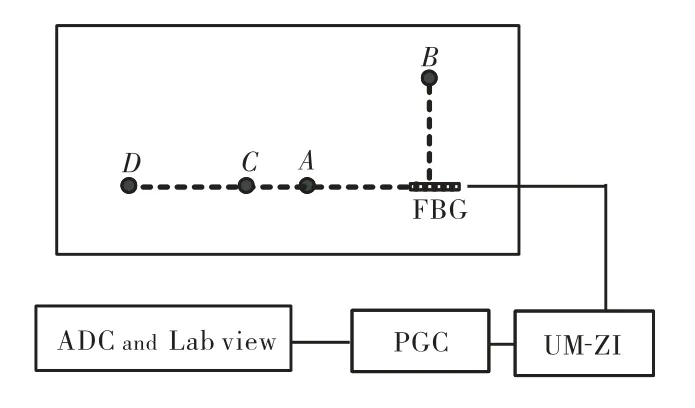
图2 FBG检测波动信号实验示意Fig.2 Block diagram of detecting wave signal by FBG

波动信号源由钢球自由落体撞击平面钢板产生，钢球每次以相同的初始动能撞击钢板即信号源的大小相同；信号源的位置分别为 A、B、C、D，其中 A、B距离FBG传感器20,cm，角度分别为0和90°；C、D距离 FBG 传感器分别为 30,cm、50,cm，角度为 0°．FBG检测到的波动信号由非平衡干涉仪(UM-ZI)和相位载波技术(PGC)进行解调[8]，解调结果通过模数转换并由Lab view软件进行处理．

对应位置A、B、C、D，检测到的波动信号分别如图 3(a)～(d)所示．

图3 波动信号检测实验结果Fig.3 Experimental results of variation signal detection

从图3可以看出，由于钢板组成材料相同即各向同性，所以图 3(a)、(b)检测到的波动信号幅值基本相同；并且图 3(a)、(c)的信号幅值也基本相同，即FBG对半径为30 cm的圆周范围内的振动信号能完全有效检测；当信号源远离FBG时，检测到的波动信号的幅值变小，如图 3(d)所示．这与图 1所示 FBG检测波动信号范围相吻合．

3.2 FBG传感器优化配置仿真实验

3.2.1 优化配置方案仿真

依据建立的优化配置准则，用改进后的自适应PSO算法仿真求解传感器优化配置问题．选取结构健康监测中常见的平板结构作为优化配置对象，如图4所示．为了便于分析将平板进行网格化，共划分为138个节点；仿真优化配置目的是将传感器配置在合适的节点位置上，使传感网络对整个监测领域的可能信号源(共 138个)的覆盖率最大，即式(3)表示的适应值最小．

图4 需优化配置传感器的平面结构网格Fig.4 Mesh diagram of plate structure for optimal sensor placement

自适应 PSO算法的参数设置为：w0= 0 .4；c1= c2= 2 .05；粒子群规模为 20个；设传感器的覆盖半径分别为 1和 3个网格单位；最大搜索次数为1,000；设适应值小于 0.01时满足覆盖率要求．需要说明的是式(4)所示的 PSO算法是针对实数运算的，但由于传感器配置位置是网格节点数即整数，因此在搜索迭代时，每次更新完粒子速度和位置后均进行取整．

仿真结果如图 5所示．当传感器数量为 36时，适应值为0.008,7，首次小于0.01．可以认为所需最少的传感器数量为35(适应值为0.012,75)，此时一种可能的传感器配置位于节点(1，5，13，16，18，20，23，26，31，33，46，47，50，52，58，63，67，78，82，84，88，92，95，99，110，111，113，115，116，120，124，126，127，128，131)上．从图 5可以看出，随着传感器数量的增加，适应值的递减梯度逐渐减小，也就是说在配置一定数量的传感器后，再增加的传感器对适应值的贡献逐渐减小．因此实际优化配置传感器时考虑到经济成本和检测设备的性能，可以更合地选择传感器数量，如此例中的传感器数量从25以后，适应值递减梯度非常小，故合适传感器数量可选25．

图5 传感器数量和优化配置的适应值的关系曲线Fig.5 Curve between number of sensors and fitness

3.2.2 改进PSO算法性能仿真

为了验证改进的自适应 PSO算法在收敛精度和速度方面的优势，仿真分析了自适应调整惯性权重和线性调整惯性权重两种 PSO算法在传感器优化配置问题求解上的性能．线性调整惯性权重是从0.9逐次减小到 0.4[7]；自适应 PSO算法参数和上述仿真参数取值相同；设传感器数量为25，两种PSO算法各运行5次，求解最优适应值，结果如表1所示．

表1 两种PSO算法对比Tab.1 Comparison of two PSO results

从表 1可以看出，在参数相同、最大搜索次数(1,000)固定的情况下，按自适应的 PSO 算法在收敛速度和收敛精度方面都要优于线性调整的 PSO算法．特别从适应值的标准差可以看出在搜索后期，自适应的 PSO算法能在更小的局部范围内搜索更优的优化解．

4 结 论

(1)通过分析FBG传感器检测波动信号的特点，建立传感器覆盖率最大化的优化配置准则并用 FBG波动信号检测实验证明了其合理性．根据标准 PSO更新算法特点，设计了一种跟随粒子群适应值分散程度自适应修改惯性权重的 PSO算法；仿真分析了平板结构的传感器优化配置问题，结果表明，改进算法在收敛精度和收敛速度上具有明显优势．

(2)仿真结果显示，由于 PSO算法求解过程中粒子位置和速度取整运算，优化算法的收敛值有一定的波动范围，为了进一步提高算法的收敛精度，可对PSO算法继续改进，如嵌入局部随机搜索方法及与遗传算法相结合等．

［1］ Kammer D C. Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance：Control and Dynamics，1991，14(2)：251-259．

［2］ Meo M，Zumpano G. On the optimal sensor placement techniques for a bridge structure[J]. Engineering Structures，2005，27：1488-1497.

［3］ 黄维平，刘 娟，李华军. 基于遗传算法的传感器优化配置[J]. 工程力学，2005，22(1)：113-117.Huang Weiping，Liu Juan，Li Huajun. Optimal sensor placement based on genetic algorithms[J]. Engineering Mechanics，2005，22(1)：113-117(in Chinese).

［4］ Gao Hudiong，Rose Joseph L. Sensor placement optimization in structural health monitoring using genetic and evolutionary algorithms[C]// Proceedings of SPIE．San Diego，USA，2006，6174(2)：310-321.

［5］ Eberhart R C，Kennedy J. A new optimizer using particle swarm theory[C]// Proceedings 6th Int Symp on Micromachine and Human Science．Nagoya，Japan，1995：39-43.

［6］ Kennedy J，Eberhart R C. Particle swarm optimization[C]//Proceedings IEEE Int Conf on Neural Networks．Perth，Australia，1995：1942-1948.

［7］ Shi Y，Eberhart R C. A modified particle swarm optimizer[C]// Proceedings of the 1998 Conf of Evolutionary Computation．Anchorage，USA，1998：69-73．

［8］ 王 为，林玉池，朱萍玉. 光纤光栅在低阻抗材料动态性能测试中的应用[J]. 光学精密工程，2009，17(3)：488-492.Wang Wei，Lin Yuchi，Zhu Pingyu. Application of FBG sensor to measurement of dynamic performance of low impedance material[J]. Optical and Precision Enginerring，2009，17(3)：488-492(in Chinese).