基于FENAP平台的钢筋混凝土桥墩非线性动力分析

禚 一，李忠献，李 宁

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

近年来，随着地震作用下桥梁结构倒塌过程模拟研究的深入，钢筋混凝土桥墩等重要构件的精细化模拟问题已越来越多地受到人们的重视.目前，构件精细化模拟分析模型主要有三维实体有限元模型和离散杆系单元模型.三维实体有限元模型虽然可以相当精细地模拟构件的一些重要非线性特征，但较高的计算成本及计算收敛问题在很大程度上限制了这种模型的发展，使之难以用于复杂桥梁结构的模拟.相比而言，离散杆系单元模型既可从宏观上模拟构件的性能又能深入分析构件的局部非线性特性，且模型简单、无需耗费大量机时，因而受到大多数研究人员的青睐[1].根据单元塑性铰分布方式和截面滞回特性模拟方法的不同，离散杆系单元分析模型又分为集中塑性模型[2-3]、分布塑性模型[4]和梁柱纤维单元模型[5-6].由于纤维模型直接从截面内纤维的本构关系出发得到单元乃至整个构件的非线性性能，可有效地模拟构件的刚度退化、强度退化等损伤效应及轴力和(单向、双向)弯矩的多维耦合效应等复杂非线性行为，因而已成为结构精细化模拟的必要手段，并得到广泛应用．

现阶段，采用纤维梁柱单元进行数值模拟，大多利用国外已有软件，如 OpenSEES[7]、DRAIN[8]等.大型通用有限元软件ABAQUS具备强大的非线性求解能力以及友好的前后处理界面，已为大多数研究人员所采用，但国内外基于 ABAQUS的纤维梁柱单元的实用开发却不多见.因此，课题组基于ABAQUS开发了一种实用的钢筋混凝土纤维梁柱单元模拟分析平台 FENAP，编制相应的材料库，开发了混凝土和钢材的本构模型，并利用 FENAP平台模拟了钢筋混凝土梁、墩柱构件的滞回性能，取得了较好的模拟结果，验证了FENAP平台进行非线性静力分析的有效性.

笔者在以往研究成果的基础上，进一步研究了纤维梁柱单元与通用有限元软件ABAQUS相结合进行非线性动力分析的基本原理，开发了 FENAP平台的非线性动力分析模块.同时，利用 FENAP平台分别模拟了桥墩单向和双向地震动作用下的动力特性，并将计算结果与OpenSEES及试验结果进行对比分析，以验证FENAP平台进行非线性动力分析的有效性.

图1 纤维梁柱单元端力、位移及截面力、变形的定义Fig.1 Definition of terminal force， displacement，cross-section force and distoration of fiber beam-column element

1 FENAP平台非线性动力分析的基本原理

在 FENAP平台中，采用了基于刚度法的三维两节点纤维梁柱单元，如图1所示.

根据经典的 Euler-Bernoulli梁柱单元理论，单元的位移场分布 ()xu~ 可用式(1)所示的单元插值函数进行描述.

式中：U为单元节点位移矢量；s()xN 为插值函数矩阵；轴向位移 ()u x采用拉格朗日线性插值；横向位移()v x、()w x分别采用三次埃米特多项式插值.在平截面假定条件下，单元截面变形 ()xd 与节点位移U的变形协调关系可表示为

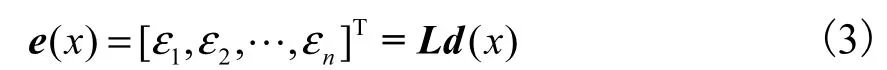
式中：iε为第i根纤维的应变，n表示纤维总数；iy、iz表示第i根纤维的中心位置坐标.L为线性几何变换矩阵，即

根据应变所在位置处纤维的材料本构关系便可计算得到相应纤维的材料切线模量iE及应力值写成矩阵形式为

式中diag()表示对角阵．对截面内所有纤维进行积分，可得到截面刚度矩阵s()xk 和抗力矢量 ()xD ，分别为

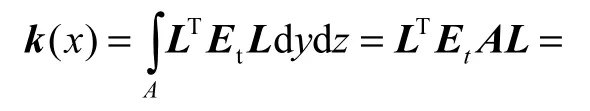
将式(2)代入式(9)，两端消去虚加位移δU后，得到单元抗力矢量为

将式(2)和式(8)代入式(10)，得到单元刚度矩阵为

FENAP平台是基于 ABAQUS/standard求解器开发的，在求解器中动力时程分析时，采用了Hilbert-Hughes-Taylor(HHT)积分算法进行迭代计算[9].HHT算法通过建立结构整体等效刚度矩阵和等效荷载矢量来计算结构的节点位移，最终得到结构的响应.因此，在单元层次上，需要进一步建立单元的等效刚度矩阵eqK 和等效抗力矢量epP.根据 HHT算法对等效刚度矩阵eqK 和等效抗力矢量eqP的定义，可得到

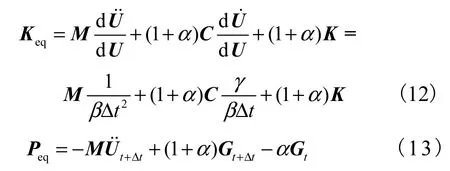
式中：M为单元质量矩阵，这里选用集中质量矩阵形式；C为阻尼矩阵，选用 Rayleigh阻尼形式；表示单元内力贡献；α、β、γ均为分析参数，1/2 γα=−，为了加快收敛，选用

2 FENAP平台材料库本构模型

FENAP平台的材料库中包含的单轴本构模型包括适用于混凝土材料的 Mohd-Yassin[10]提出的混凝土损伤本构模型和适用于钢筋材料的理想弹塑性本构模型、双线性等向强化本构模型和Filippou等[11]修正的 Menegotto-Pinto本构模型[12]等.其中，修正的Menegotto-Pinto本构模型为课题组近期开发的，可考虑钢筋反复加载过程中的Bauschinger效应和等向强化效应，并且在计算过程中，采用应变的显函数表达形式求解应力和切线模量，因而具有较高的计算精度，与钢筋反复加载试验结果吻合较好，其循环加载滞回曲线如图2所示.

图2 Menegotto-Pinto钢筋本构模型循环加载滞回曲线Fig.2 Cyclic hysteretic curves of Menegotto-Pinto steel Fig.2 constitutive model

3 模拟分析

为验证应用FENAP平台进行非线性动力分析的有效性，将模拟分析钢筋混凝土桥墩在单向地震激励下的数值试验和钢筋混凝土桥墩在双向地震激励下的振动台试验.

3.1 钢筋混凝土桥墩在单向地震激励下的数值试验

分别利用 FENAP平台和 OpenSEES软件对一RC桥墩在单向加载下的地震响应进行了数值模拟.该桥墩高 2.265,m，矩形截面 400,mm×800,mm.在FENAP建模过程中，将桥墩划分为10个纤维梁柱单元，共计11个节点，每个单元采用两个Gauss积分截面，截面内由 24根保护层混凝土纤维、32根核心混凝土纤维以及24根钢筋纤维组成.其中，混凝土纤维均采用 FENAP材料库中的混凝土损伤本构模型，其材料参数包括混凝土的初始弹性模量c0E 、峰值压应力cf′、相应的压应变0ε、极限压应变uε、峰值拉应力和抗拉刚化模量tsE .箍筋对核心混凝土的约束作用通过提高核心混凝土的材料本构参数来实现.表 1给出了保护层和核心混凝土的材料特性参数.钢筋纤维采用 FENAP材料库中的双线性等向强化本构模型，其材料特性参数包括初始弹性模量 Es、屈服强度fy和屈服后刚度系数b，如表 2所示.图 3给出了单元划分及截面纤维离散化方式.OpenSEES建模过程中，单元及截面纤维的划分方式与 FENAP一致，每个单元设为5个积分截面，并选用Concrete01模型模拟混凝土纤维的本构，Steel01模型模拟纵筋纤维的本构，相应材料的强度和应变参数也与FENAP相同.

表1 混凝土材料特性Tab.1 Material properties of concrete

表2 钢筋材料特性Tab.2 Material properties of steel

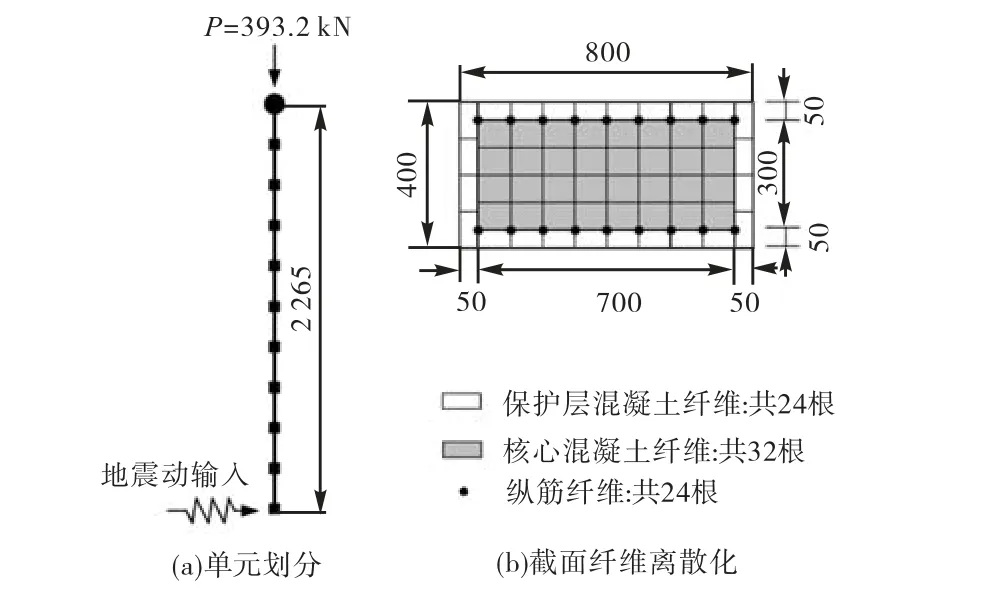
图3 单元划分及截面纤维离散化Fig.3 Element division and cross-section fiber discretization

分析过程中，选用 El-centro波南北向在墩底进行单向加载，为了得到结构的非线性响应，将地震动峰值调整为0.312g，图4、图5分别给出了FENAP平台和 OpenSEES计算得到的墩顶位移时程和墩底截面弯矩-曲率关系对比曲线，比较结果可看出，FENAP平台得到的位移时程响应的相位变化和幅值大小与OpenSEES的结果十分吻合．FENAP计算得到的墩顶位移最大值为 34.1,mm，发生在 6.268,s处，而OpenSEES计算得到的墩顶位移最大值为33.47,mm，发生在6.26,s处．另外，即使进入非线性状态后，截面弯矩-曲率关系曲线的形状和包围面积的耗能，二者也给出了十分接近的分析结果．进一步研究发现，对于该算例OpenSEES计算用时为908,s，而FENAP仅用时 746,s就得到了收敛的计算结果，这更加验证了FENAP平台在保证求解精度的同时还具备较高的计算效率.

图4 墩顶相对位移时程对比曲线Fig.4 Comparison of relative displacement time history at top of bridge pier

图5 墩底截面弯矩-曲率对比曲线Fig.7 Comparison of moment-curvature curves at bottom Fig.7 of bridge pier

3.2 桥墩在双向地震激励下的振动台试验

文献[13]对一方形截面钢筋混凝土桥墩进行了双向加载振动台试验，笔者采用 FENAP平台对其进行数值模拟分析.建模过程中，沿桥墩纵向划分为10个纤维梁柱单元和2个刚体单元，并在墩顶配重的形心位置布置一个质量点单元，用于模拟上部结构的等效质量，如图 6所示.在纤维单元中，将截面划分为 144根核心混凝土纤维、112根保护层混凝土纤维和 48根钢筋纤维，混凝土纤维采用 FENAP材料库中的混凝土损伤本构模型，强度为 34.1,MPa；钢筋纤维采用FENAP材料库中的修正Menegotto-Pinto本构模型，强度为384,MPa，其他材料参数按照文献[13]选取.加载时，选用Kobe波的东西和南北向同时在墩底输入，并按时间相似比0.5对原记录进行压缩，地震波东西和南北向峰值加速度分别取为0.666g和0.642g.

图7、图8分别给出了FENAP平台和文献[13]中作者数值模拟结果及试验结果的对比曲线．与文献[13]的模拟结果比较，FENAP平台模拟结果与试验曲线较为接近.在3,s之前，FENAP平台与试验曲线基本吻合.对于x和y方向的峰值响应出现时间和大小两者并无较大差别.因此，对于结构在未进入塑性状态前，FENAP平台可以给出较为准确的预测结果；经过峰值点，构件完全进入到塑性状态后，FENAP平台结果与试验结果偏差较大，试验得到的位移明显大于分析结果，其主要原因在于进入塑性阶段后，钢筋和混凝土间发生的黏结滑移会降低构件的刚度，增大位移响应，而 FENAP中所采用的纤维模型基本原理是在平截面假定基础上建立的，并未考虑黏结滑移的影响，因而得到的位移响应较试验结果偏小.另一方面，由双向位移耦合曲线的对比结果可看出，与文献[13]得到的双向位移耦合曲线相比，FENAP平台得到的双向加载下的位移发展方向和曲线的形状与试验是较为吻合的.

图6 桥墩单元划分及截面纤维离散化Fig.6 Element division and cross-section fiber discretization of bridge pier

图7 墩顶相对位移时程响应曲线Fig.7 Time history of relative displacement at top of bridge pier

图8 双向位移耦合曲线Fig.8 Coupled curves of bilateral displacement

为进一步比较在FENAP平台中考虑双向弯曲耦合作用对动力结果的影响，将上述桥墩试件所采用的东西向和南北向地震波，分别在试件的两个垂直方向单独施加，以模拟单向地震动加载情况，从而对桥墩在单向加载与双向加载条件下的数值模拟结果进行对比研究.计算得到的单向和双向耦合的相对位移和绝对加速度时程对比曲线如图9和图10所示.

图9 单向和双向加载位移时程响应对比Fig.9 Comparison of time histories of displacement between unilateral and bilateral excitation

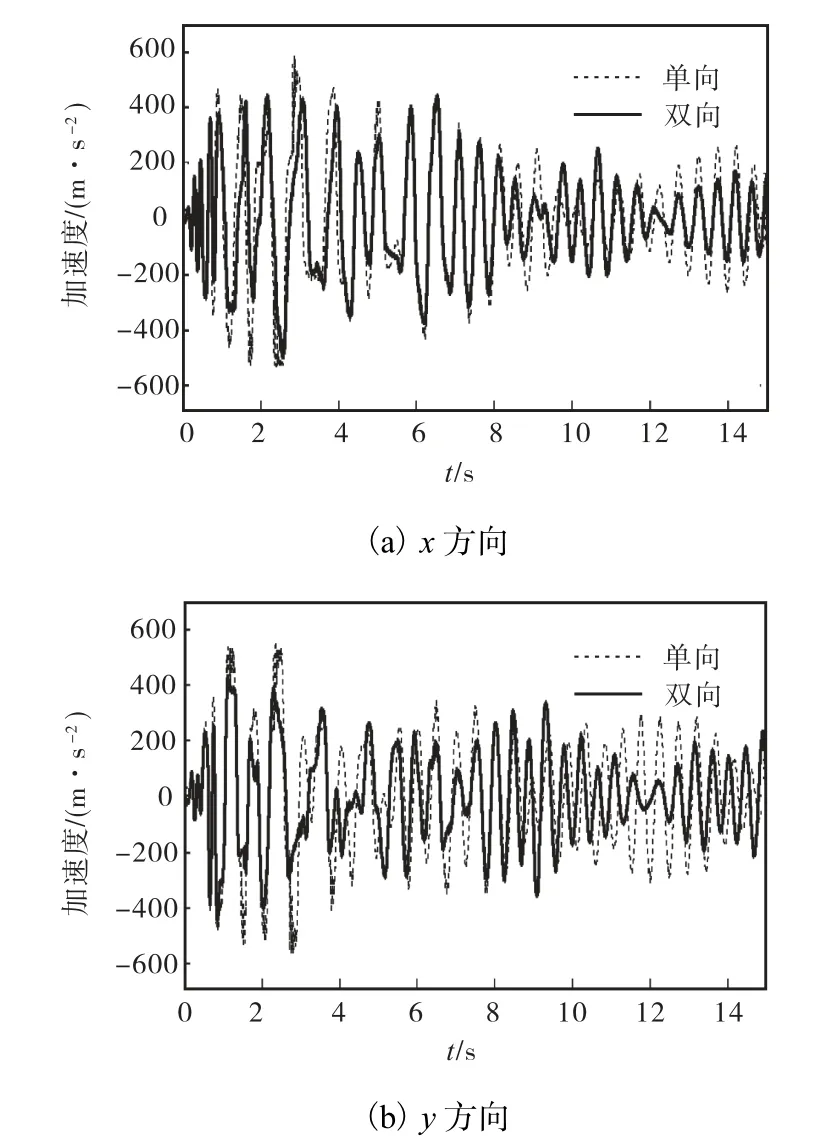
图10 单向和双向加载加速度时程响应对比Fig.10 Comparison of time histories of acceleration between unilateral and bilateral excitation

结果显示，双向地震下得到的位移响应结果大于单向(x方向加载位移峰值仅为双向加载时的63.3%，y方向仅为双向加载时的 82.2%)，而双向地震下得到的加速度响应小于单向(x方向单向加载加速度峰值为双向加载时的1.354倍，y方向为双向加载时的1.216倍)，可见，FENAP平台可有效模拟双向弯曲耦合作用对结构动力响应的影响，反映其真实抗震性能.

4 结 语

基于 FENAP平台所开发的非线性动力分析模块，充分发挥了 ABAQUS求解器的强大非线性动力分析功能，可有效模拟钢筋混凝土桥墩的复杂非线性动力行为，可考虑双向弯矩和轴力的耦合效应，且具有较高计算效率和求解精度，从而为长大桥梁结构地震灾变过程模拟提供了一种实用分析手段.

［1］ Taucer F F，Spacone E，Filippou F C. A Fiber Beamcolumn Element for Seismic Response Analysis of Reinforced Concrete Structures[R].Berkeley：Earthquake Engineering Research Center，University of California，1991.

［2］ Powell G H，Chen P F S．3D beam-column element with generalized plastic hinges[J]. Journal of Engineering Mechanics，ASCE，1986，112(7)：627-641.

［3］ Sfakianakis M G，Fardis M N. Bounding surface model for cyclic biaxial bending of RC sections[J]. Journal of Engineering，Mechanics，ASCE，1991，117(12)：2748-2769.

［4］ Roufaiel M S L，Meyer C. Analytical modeling of hysteretic behavior of R/C frames[J]. Journal of Structural Engineering，ASCE，1987，113(3)：429-444.

［5］ Spacone E，Filippou F C，Taucer F F. Fibre beam-column model for non-linear analysis of R/C frames(Part I)：Formulation[J]. Earthquake Engineering and Structural Dynamics，ASCE，1996，25(7)：711-725.

［6］ Spacone E，Filippou F C，Taucer F F. Fibre beam-column model for non-linear analysis of R/C frames(Part Ⅱ)：Applications[J]. Earthquake Engineering and Structural Dynamics，1996，25(7)：727-742.

［7］ Mckenna F，Fenves G L. The OpenSEES command language manual[EB/OL]. http：//opensees. berkeley. edu/wiki/index. php/Main_Page，2010-03-31.

［8］ Prakash V，Powell G H，Campbell S D. DRAIN-2DX：Static and Dynamic Analysis of Inelastic Plane Structures[R]. Berkeley：Earthquake Engineering Research Center，University of California，1993.

［9］ ABAQUS Inc. ABAQUS User Subroutines Reference Manual[M]. Rhode Island：ABAQUS Inc，2006.

［10］ Mohd-Yassin M H. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cyclic Loads[D]. Berkeley：School of Civil and Environmental Engineering，University of California，1994.

［11］ Filippou F C，Popov E P，Bertero V V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints[R]. Bekerley：Earthquake Engineering Research Center，University of California，1983.

［12］ Menegotto M，Pinto P E，Slender R C. Compressed members in biaxial bending[J]. Journal of Structural Division，ASCE，1977，103(3)：587-605.

［13］ Nishida H，Unjoh S. Dynamic response characteristic of reinforced concrete column subjected to bilateral earthquake ground motions[C]// 13th World Conference on Earthquake Engineering．Vancouver，Canada，2004：576-587.