基于Copula方法的干旱历时和烈度的联合概率分析

许月萍，张庆庆，楼章华，刘德地

(浙江大学建筑工程学院水文与水资源研究所，杭州 310058)

水文干旱极限分析一直是水文学家及水资源决策者共同关心的问题之一，近几年来，随着全球气候变化，干旱事件发生的频率和强度增加，研究极限干旱事件越发重要．干旱事件通常有 3个重要指标，即干旱历时、烈度和间隔时间．然而，分析干旱事件往往只关注干旱的历时或干旱烈度，如冯国章[1]应用独立同分布随机变量序列最大负游程长的概率分布函数进行极限干旱历时最大干旱持续时间的概率分析；丁晶等[2]分析了作为水文干旱定量指标负轮长的统计变化特性，并以哈尔滨和陕县站为例，应用随机模拟方法探讨了严重干旱出现可能性的定量估计方法；朱廷举等[3]探讨了严重水文干旱事件的发生规律和确定黄河上中游地区连续枯水段的发生概率和重现期；袁超等[4]研究了 P-Ⅲ分布和马尔可夫过程年径流序列极限水文干旱历时概率分布随水文参数的变化规律．对于干旱事件，干旱历时、干旱烈度甚至间隔时间都非常重要，目前针对这三者的多元变量分析在国内外已经引起了充分重视，如González等[5]应用经典多元变量分析方法建立了边际分布分别为几何和伽马分布的干旱历时和干旱烈度两元概率分布；Shiau等[6]则应用 Copula方法建立了边际分布分别为混合指数和伽马分布的历时和强度两元概率分布．鉴于干旱数据短缺，笔者利用自回归马尔可夫模型对水文序列进行延长，在此基础上，应用Copula方法对干旱发生的历时和强度的概率分布进行定量研究，并以浙江省钱塘江流域诸暨水文站的年降雨序列为例，分析了此方法的实际可行性．

1 研究方法

因干旱时间序列短，直接对短序列进行分析往往不确定性比较大．采用两步骤来对干旱进行分析．第1步是通过自回归马尔可夫模型对水文序列进行延长，以解决短序列不确定性大的问题．第 2步是利用Copula方法对多变量水文数据进行分析，考虑多变量之间的相依性．

1.1 干旱的定义

对水文干旱进行分析，一般采用 Yevjevich[7]的游程理论．图 1为干旱定义的示意图，水文极限干旱事件一般定义为所关注的水文气象变量处于某一截取水平R0以下的时期．此截取水平可为常数，也可随时间变化．可以看出干旱事件 3个重要指标即干旱历时、烈度和间隔时间的定义．

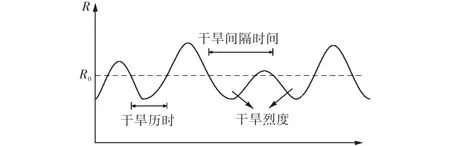
图1 干旱事件的定义Fig.1 Definition of drought event

1.2 自回归马尔可夫模型

研究极限事件，最主要的困难是资料不足，水文干旱事件同样如此．为揭示水文干旱的基本规律，利用现有观测序列所包含的统计信息进行随机模拟．假定水文序列是一个马尔可夫过程，并服从正态分布．利用下面的模型就可以生成均值为μ、方差为2σ、逐年相关系数为ρ的正态分布的径流量序列．

式中：y1v+为独立标准正态随机变量；ρ为相关系数；σ为标准差；μ为均值；1yQ+为 1y+时刻的径流量．

然而水文序列有时候并不适宜用正态分布来描述，调整式(1)中随机成分的偏差以使模型生成的水文序列具有相应的均值、方差和偏差系数，也即保持序列的部分统计特性[8]．这里利用标准化的χ2分布随机数ξ来实现．当χ2分布的自由度大于 30时，ξ与标准正态的随机数之间的关系为

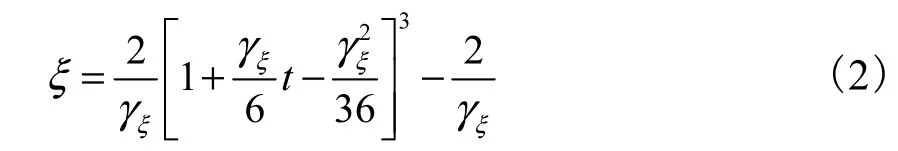
式中ξγ为ξ的偏差系数，与水文序列偏差系数Qγ的关系为

因此，偏态水文序列的自回归马尔科夫模型为

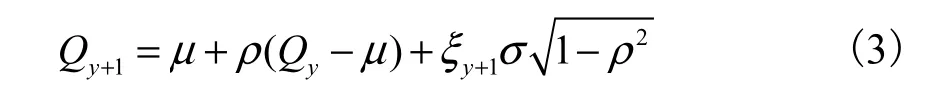
1.3 Copula方法

1.3.1 Copula方法简述

Copula作为一种全新的相关性度量工具，由Sklar在1959第一次提出．Sklar定理是Copula领域中最重要的一个定理，它证明了 Copula存在的唯一性．假设X和 Y是两个随机变量，它们的联合分布函数为G(x，y)，边缘分布函数分别为Fx(x)和Fy(y)，则一定存在着一个联结函数 Copula C，满足 G(x，y)＝C(Fx(x)，Fy(y))．如果 Fx(x)和 Fy(y)是连续的，那么C 是唯一的．相反，如果 C 是一个 Copula，Fx(x)和Fy(y)是分布函数，则由 G(x，y)＝C(Fx(x)，Fy(y))所定义的 G(x，y)是一个联合分布函数，而其边缘分布函数分别是Fx(x)和Fy(y)．

可用来描述极限情况下的多变量相依关系的Copula 有 Archimedean Copula、Farlie-Gumbel-Morgenstern Copula、Joe BB1 Copula和 Joe BB5 Copula等．Copula方法因数学表达上比较简洁，各个变量之间的相依结构和边缘分布可以独立考虑，所以其在国内外水文学中的应用日渐增加[9-12]．作为水文干旱极限分析探索性的研究，笔者应用 Archimedean联结函数中的 Clayton Copula．它可以用来描述变量之间的正相依性，而且适合用来模拟尾部，也即极限事件．以双变量为例，Clayton Copula的概率分布为

而经验Copula定义为

式中：n为序列长度；l为指示函数．

1.3.2 Copula拟合检验

判断Clayton Copula方法能否很好地描述相依变量间的概率分布，通常是通过比较所用 Copula跟经验 Copula的距离来完成的，用 Kolmogorov-Smirnov(KS)统计量来做拟合检验．KS统计量计算公式为

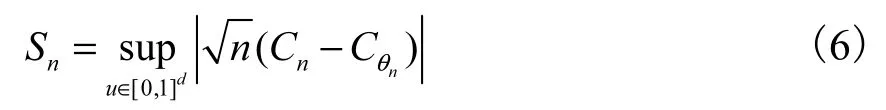
利用自助抽样 Bootstrap法来计算 KS统计量，具体步骤为：

根据观测样本计算Clayton Copula的参数θ；

根据式(5)计算经验CopulaCn的值；

根据式(6)计算KS统计量 Sn的值；

选用一个较大的整数 N，对每一个 k ∈ { 1,… ,N }重复以下步骤，即

(1)从Cθ里面产生随机数，并计算相应的，这里为生成序列的秩；

如果通过自助抽样法计算出来的P值太大，则假设不成立，即所用的 Copula模型不能很好地模拟多变量之间的相关关系．P值是进行检验决策的依据，即概率反映某一事件发生的可能性大小．

1.3.3 联合概率分布计算

利用 Copula函数，计算X和Y联合概率分布为

2 应 用

采用浙江省钱塘江流域上诸暨站的年降雨量数据，从 1951—2003年一共 53年．多年来浙江省资源型、水质型和工程型缺水并存，据预测，浙江省在现状情况下，如遭遇一般干旱年，将缺水 6亿 m3，如遭遇大旱年份，将缺水23亿m3．到 2010年，随着工业的发展、城市化率和人民生活水平的提高，如不增加水源建设，遭遇一般干旱年，将缺水71亿m3，如遭遇大旱年份，将缺水90亿m3．因此，对水文干旱情况进行分析至关重要，可为浙江省水资源的有效管理提供技术支持．

2.1 干旱历时和烈度数据获取

图2所示为钱塘江诸暨站的年降水量序列，其多年平均降雨量约为1,400,mm．从图2中可以看出，诸暨站枯水和丰水常成组出现，这说明年降雨量时间序列存在着正相依性．假如以多年平均降雨量为截取水平，可以看到诸暨站很多年份都处于缺水状态．

图2 诸暨站的年降雨量时间序列Fig.2 Annual precipitation time series at Zhuji station

图3所示为诸暨站利用自回归马尔可夫模型生成的1,000年年降雨数据(截取水平为1,400,mm)，表1为模拟数据跟实际数据主要统计特征值．可以看出，自回归马尔可夫模型较合理地保持了实测年降雨序列的基本统计信息值．

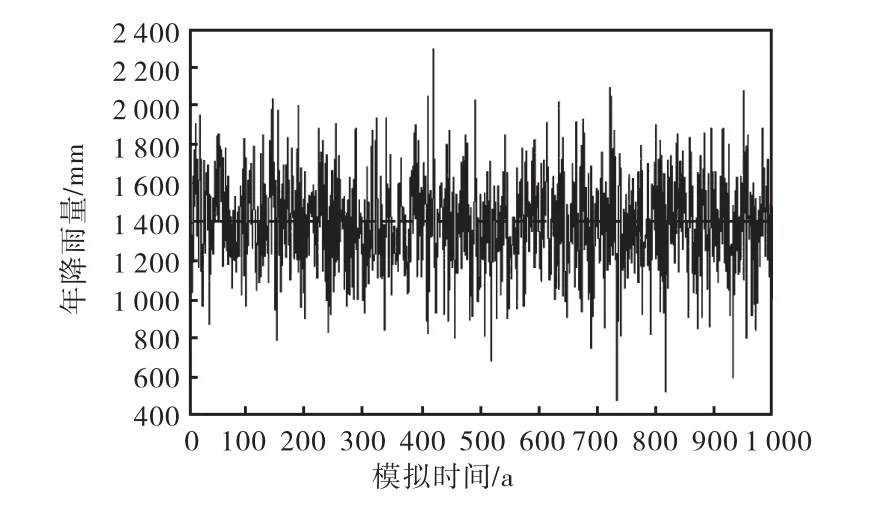
图3 自回归马尔可夫模型模拟结果Fig.3 Simulation results of autoregressive Markov model

表1 模拟结果与实测数据基本统计特性比较Tab.1 Comparison of simulation and actual data statistics

选取多年平均降雨量作为截取水平，由图1可获得干旱历时、干旱烈度和间隔时间数据，系列长度为243年．表 2为干旱历时、烈度和间隔时间的一些基本统计信息，可看出这些变量并不遵循正态分布．

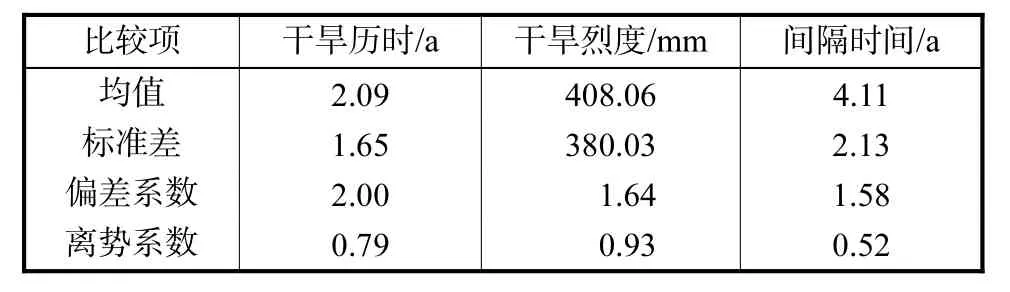
表2 干旱历时、烈度和间隔时间的一些基本统计特性Tab.2 Basic statistics of drought duration，severity and Tab.2 interval time

选取干旱历时和烈度两个变量来做干旱分析，图4所示为两变量之间的相关关系，可以看出两者呈现较大的正相关关系．经计算，其Kendall秩相关系数τ为 0.70．

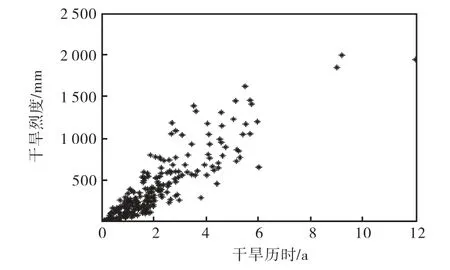
图4 干旱历时和烈度相关关系Fig.4 Relationship of drought duration and severity

2.2 拟合检验

采用Joe[13]提出的IFM方法，先估计边际函数及其参数，然后估计Copula的参数．应用线性距比例图得出，干旱历时符合皮尔逊Ⅲ型曲线，干旱烈度符合伽马分布函数．皮尔逊Ⅲ型和伽马分布函数的公式分别为和()f x=其中Γ为伽玛函数，α、β、a0均为皮尔逊Ⅲ型曲线的3个参数，α1、β1分别为伽马分布函数的两个参数．用 Kolmogorov-Smirnov检验两者的适用性，计算得出P分别为0.01和0.04．取置信水平 5%，则两者都小于临界值，因此假设成立．利用线性距方法估计得出：α =1.52,β =0.77,a0=0.13(皮尔逊Ⅲ型曲线的3个参数)，α1= 3 54.04，β1= 1 .15(伽马分布函数的两个参数)．

利用自助抽样法计算Kolmogorov-Smirnov统计量来检验Clayton Copula的适用性，采用N＝1 000，得出P值为0.001，由此可见，Clayton Copula可以很好地描述干旱历时和烈度的相依性．因 Kendall秩相关系数τ约为0.70，Clayton Copula的参数为

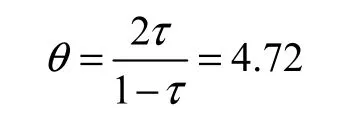
2.3 结果分析

以皮尔逊曲线和伽马函数分别为干旱历时和干旱烈度的边际函数、Clayton Copula为联结函数，对钱塘江诸暨站的干旱情况做出模拟．图 5和图 6分别为 Copula函数及干旱历时和干旱烈度的两元联合分布等值线图，可以看出两变量存在强相依关系．从图5和图 6即可查出干旱历时和强度发生各种组合的联合分布，例如，可以查出干旱历时为3年时，干旱烈度为600,mm的概率为 69%，从而可以定量得出干旱烈度和干旱历时发生各种组合的概率．

图5 Copula函数及相应的等值线Fig.5 Copula and corresponding level curves

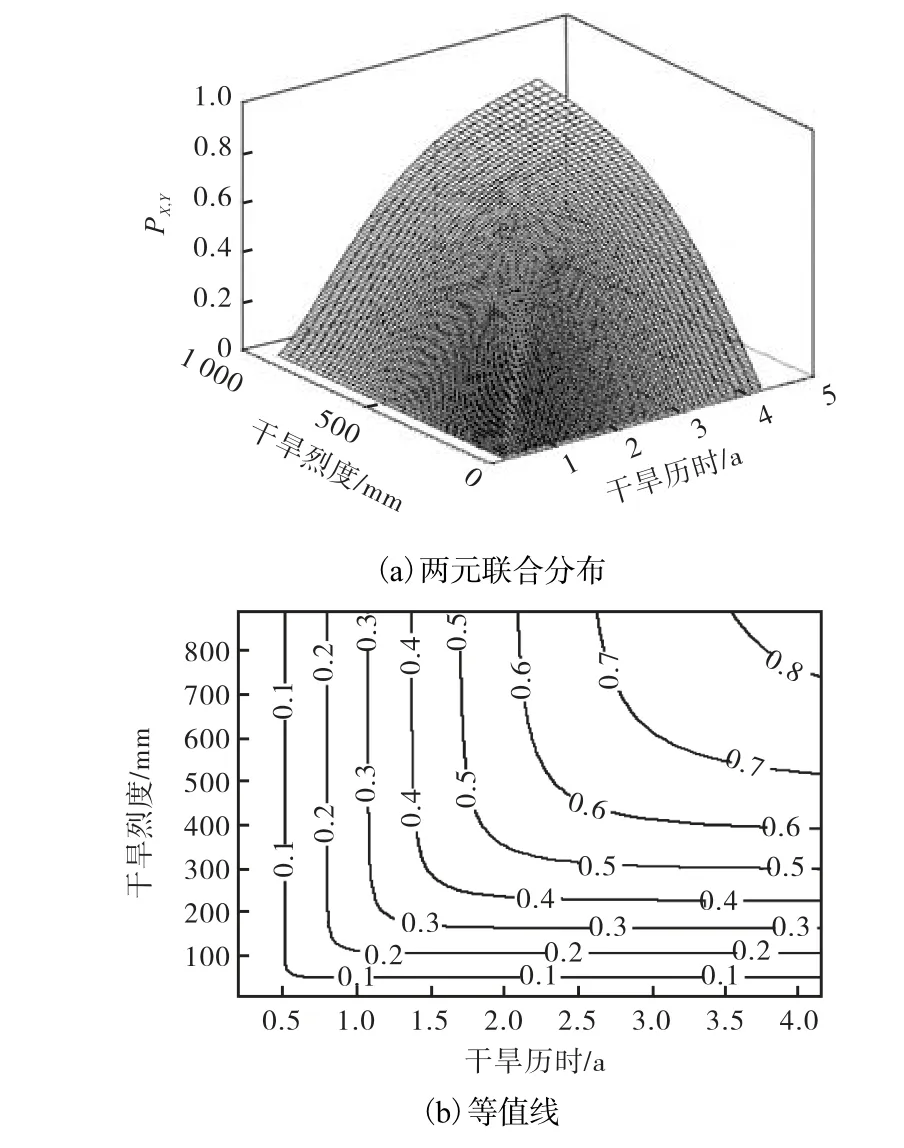
图6 干旱历时和干旱烈度的两元联合分布及其等值线Fig.6 Joint distribution of drought duration and severity and corresponding level curves

表 3为一些典型干旱历时与烈度的联合概率值，即 PX,Y(X ≤ x , Y ≤ y )的值．此联合概率值可为流域/地区的水资源的有效管理提供强有力的技术支持．

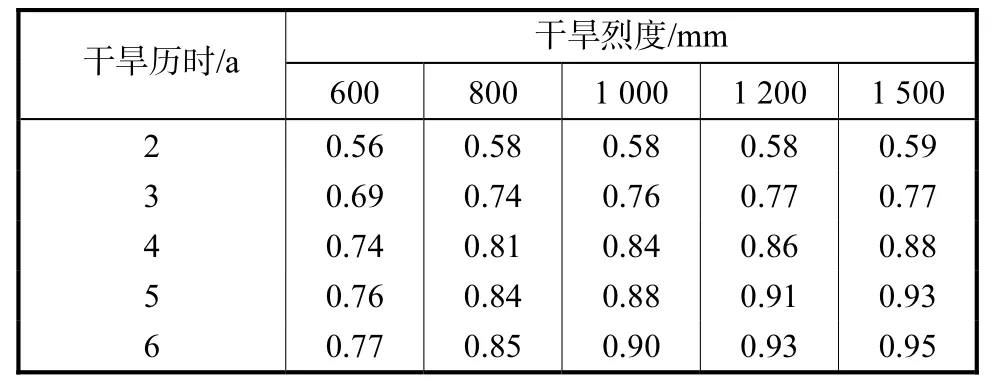
表3 不同干旱历时与烈度的联合分布Tab.3 Joint distribution for various combinations of drought durations and severity

3 结 论

(1)利用自回归马尔可夫模型来延长水文干旱数据，可以解决干旱数据稀少的问题，在本文中，自回归马尔可夫模型较好地模拟了偏态的年降雨序列．

(2)Clayton Copula可以很好地模拟正相依的干旱数据，是分析极限干旱事件的有用工具．

(3)选用的截取水平也可根据具体的水资源情况来确定，如实际气象、农业或水文干旱发生时的降雨值，不一定是个定值．

［1］ 冯国章. 极限水文干旱历时概率分析[J]. 水利学报，1995，6：37-41，50.Feng Guozhang. An analysis of frequency of critical hydrologic drought duration[J]. Journal of Hydraulic Engineering，1995，6：37-41，50(in Chinese).

［2］ 丁 晶，袁 鹏，杨荣富，等. 中国主要河流干旱特性的统计分析[J]. 地理学报，1997，52(4)：374-381.Ding Jing，Yuan Peng，Yang Rongfu，et al. Stochastic analysis of the drought properties of thema in rivers in China[J]. Acta Geographica Sinica，1997，52(4)：374-381(in Chinese).

［3］ 朱廷举，胡和平. 基于随机模拟和模糊聚类的水文干旱特性分析[J]. 清华大学学报：自然科学版，2001，41(8)：101-106.Zhu Tingju，Hu Heping. Drought analysis based on stochastic simulation and fuzzy classification[J]. Journal of Tsinghua University：Natural Science Edition，2001，41(8)：101-106(in Chinese).

［4］ 袁 超，宋松柏，荆 萍. 极限水文干旱历时概率分布解析法研究[J]. 西北农林科技大学学报：自然科学版，2008，36(7)：212-218.Yuan Chao，Song Songbai，Jing Ping. Analytical study on probability distribution of critical hydrological drought duration[J]. Journal of Northwest A and F University：Natural Science Edition，2008，36(7)：212-218(in Chinese).

［5］ González J，Valdés J B. Bivariate drought recurrence analysis using tree ring reconstructions[J]. Journal of Hydrological Engineering，2003，8(5)：247-258.

［6］ Shiau J T，Feng S，Nadarajah S. Assessment of hydrological droughts for the Yellow River，China，using Copulas[J]. Hydrological Processes，2007，21(16)：2157-2163.

［7］ Yevjevich V. Stochastic Processes in Hydrology[M]. Fort Collins：Water Resources Publications，1972.

［8］ 翁文斌，王忠静，赵建世. 现代水资源规划：理论、方法和技术[M]．北京：清华大学出版社，2007.Weng Wenbin，Wang Zhongjing，Zhao Jianshi. Advanced Water Resources Planning：Theory，Method and Technology [M]. Beijing：Tsinghua University Press，2007(in Chinese).

［9］ 熊立华，郭生练，肖 义，等. Copula联结函数在多变量水文频率分析中的应用[J]. 武汉大学学报：工学版，2005，38(6)：16-19.Xiong Lihua，Guo Shenglian，Xiao Yi，et al. Application of Copula to multivariate hydrological frequency analysis[J]. Engineering Journal of Wuhan University：Engineering Science，2005，38(6)：16-19(in Chinese).

［10］ Zhang L，Singh V P. Bivariate flood frequency analysis using the Copula method[J]. Journal of Hydrological Engineering，2006，11(2)：150-164.

［11］ 肖 义，郭生练，熊立华，等. 一种新的洪水过程随机模拟方法研究[J]. 四川大学学报：工程科学版，2007，39(2)：55-60.Xiao Yi，Guo Shenglian，Xiong Lihua，et al. A new random simulation method for constructing synthetic flood hydrographs[J]. Journal of Sichuan University：Engineering Science Edition，2007，39(2)：55-60(in Chinese).

［12］ 许月萍，李 佳，曹飞凤，等. Copula在水文极限事件分析中的应用[J]. 浙江大学学报：工学版，2008，42(7)：1119-1122.Xu Yueping，Li Jia，Cao Feifeng，et al. Applications of Copula in hydrological extreme analysis[J]. Journal of Zhejiang University：Engineering Science，2008，42(7)：1119-1122(in Chinese).

［13］ Joe H. Asymptotic efficiency of the two-stage estimation method for Copula-based models [J]. Journal of Multivariate Analysis，2005，94(2)：401-419.