基于复杂网络理论的作战体系节点重要性分析

李茂林，龙建国，张德群

（1.海军指挥学院，江苏 南京 210016；2.军事科学院军事运筹分析研究所，北京 210016）

随着战争形态由机械化战争向信息化战争转变，体系对抗成为作战的主要样式和基本理念。为了准确判定作战体系的关键节点，节点重要性分析变得尤为重要。一般而言，作战体系节点重要性分析需要采用定性定量相结合的方法进行，既需要充分利用指挥决策者的经验和知识，同时要借助相关的模型和工具进行计算。但是，由于信息化条件下作战体系节点信息量非常庞大，节点之间相互作用非常复杂，决策者仅凭自己以往经验进行分析判断，很难做出正确的决策。

近年来，复杂网络理论得到了国内外研究者的广泛关注，在数理科学、生命科学、社会科学、技术科学和管理科学等众多学科中都掀起了研究和应用的热潮，被称为“网络的新科学”[1]。本文尝试将复杂网络理论应用于作战体系节点重要性分析领域，在对作战体系结构进行网络描述的基础上，根据节点重要性指标对节点的重要程度进行度量，并根据作战体系受到攻击后的受损程度对重要性指标的有效性进行分析。

1 作战体系结构的基本特征和网络描述

机械化战争时代，在通信手段和指挥控制手段受限的情况下，作战体系采取节点中心模式进行构建，即将所有作战力量分解为若干作战集团，这些作战集团保留一部分机动力量后，其余力量又分别向下分解为若干小的作战集团或作战集群，照此依次向下划分，形成了一种树状结构。随着指挥信息系统的功能越来越强，信息传输更加迅捷，战场网络更加拓展，作战体系的构建逐步转为网络中心模式，即借助高效的信息网络，将广泛分布于战场的各种节点实现有效连接，作战体系任何两个节点之间均可以根据需要建立联系，各种联系纵横交错，逐步形成网络化结构[2]。

依据复杂网络理论，可以定义作战体系由节点集合V和边集合E组成的图 G ＝ ( V,E)。其中，V＝｛v1, v2,…,vn｝，代表组成作战体系的指挥控制节点、预警侦察节点（包括战场态势信息源节点和目标信息源节点）、攻防交战节点等； E ＝｛e1, e2,…,em｝，代表节点之间信息传递关系[3]。

图1为具有一定信息化程度作战体系的网络拓扑图。该作战体系包含100个节点，362对节点之间存在信息传递关系。其中，空心圆形节点代表核心指挥控制节点，实心圆形节点代表一般指挥控制节点，三角形节点代表攻防交战节点，空心方形节点代表战场态势信息源节点，实心方形节点代表目标信息源节点。

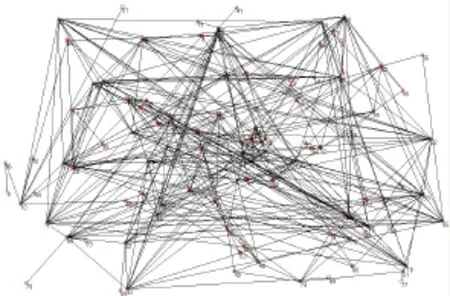
图1 作战体系的网络拓扑图

2 作战体系节点重要性的度量指标和结果

2.1 节点重要性指标

不同类型的复杂网络可以用不同的指标衡量网络节点的重要程度，比如度指标、介数指标、紧密度指标、特征向量指标[4]等。作战体系作为一种典型的复杂网络，同样可以使用这些指标对节点的重要性进行度量。

2.1.1度指标

度指标是研究网络拓扑结构的基本参数，用于描述在静态网络中节点所产生的直接影响力。根据节点度的定义，将节点i的度指标定义为：

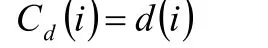
式中， d （ i）表示节点i的度。

为了根据度指标来比较不同规模网络中节点的重要性，需要对度指标进行归一化处理。具有n个节点的网络中，节点的度不会超过 n - 1，故归一化的度指标定义为

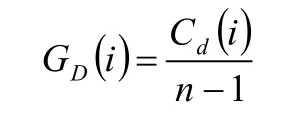
2.1.2介数指标

介数指标是指网络中最短路径通过该节点的数量，反映的是节点在网络中的枢纽性。设网络具有n个节点，则节点i的介数指标定义为

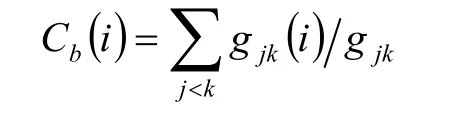
式中，gjk表示节点 j和节点k之间的最短路径数，gjk（x ）表示节点j和节点k之间经过节点i的最短路径数。

具有n个节点的网络中，对于给定节点i来说，最为极端的情形是任意两个其它节点之间的最短路径均经过该节点，此时该节点的介数指标达到最大值（n- 1 ）（ n - 2）2，故归一化的介数指标可以定义为

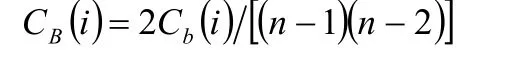
2.1.3紧密度指标

紧密度指标用于刻画网络中的节点通过网络到达网络中其它节点的难易程度，其值定义为该节点到达所有其它节点的距离之和的倒数。设网络具有n个节点，则节点i的紧密度指标定义为：

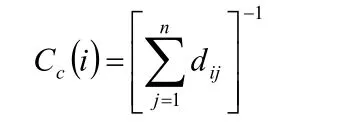
式中，dij表示节点i到节点j之间的距离。

具有n个节点的网络中，节点到达所有其它节点的距离之和不会小于n-1，故归一化的紧密度指标定义为

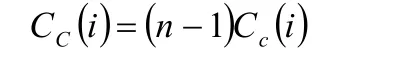
2.1.4特征向量指标

一个节点的度指标描述了该节点对于其它节点的直接影响力，若一个节点与另一个度值很高的节点之间存在连接，则该节点的影响力也应该很大，可以引入特征向量指标来分析这种通过具有高度值的相邻节点所获得的间接影响力。

设网络具有n个节点，其邻接矩阵记为A，λ为A的主特征值，e ＝ （ e1, e2,… ,en）为矩阵A对应的 λ 的特征向量。节点i的特征向量指标定义为

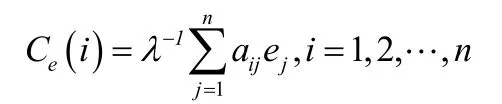
2.2 节点重要性的度量结果

使用度指标、介数指标、紧密度指标和特征向量指标分别对图1所示作战体系节点的重要性进行了度量。表1列举了重要性位于前20位的节点的序号。

表1 节点重要性的度量结果

3 作战体系节点重要性指标有效性分析

从表1可以看出，不同指标对节点重要性的度量结果存在着一定的差别，那么选择哪种指标能够更有效地衡量作战体系中节点的重要程度，便成为作战体系节点重要性分析的另一问题。

3.1 指标有效性的衡量标准

按照重要性指标对节点的重要程度进行度量后，如果按照节点重要性的大小对作战体系进行攻击，伴随着节点受损，作战体系中某些节点之间无法进行信息交换，必将导致整个作战体系分裂为很多相互独立的连通分支。根据Albert和Border等人的研究成果，可以利用最大连通分支的大小（S）和平均路径长度（L）这两个拓扑属性度量作战体系的受损程度[5]。

最大连通分支的大小指的是相对大小，即最大连通分支的节点数与所有节点数的比值。

平均距离长度定义为：

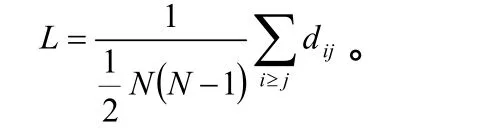
其中，N为节点数；dij为任意两个节点i和 j之间的距离，即连接这两个节点的最短路径上的边数。

因此，为了选取适用于度量作战体系中节点重要性的指标，可以按照不同指标的度量结果对作战体系进行攻击实验，即按照重要性指标值从大到小的顺序删除该节点和与之相连的所有边，根据为了达到一定受损程度而必须攻击重要节点数量的多少，来衡量不同重要性指标度量节点重要程度的有效性。

3.2 重要性指标有效性分析

根据度指标、介数指标、紧密度指标和特征向量指标对图1所示作战体系节点重要性的度量结果，对作战体系进行攻击实验，并对最大连通分支的大小（S）和平均路径长度（L）随删除节点比例f的变化情况进行了仿真分析，进而对作战体系中重要性指标的有效性进行分析。

作战体系受到攻击分裂成多个连通分支，势必引起最大连通分支大小的降低。因此，可以从f增大时，S下降的速度说明重要性指标的有效性。从图2可以看出，在 f从0增大到0.62的过程中，根据介数指标的度量结果删除节点，S下降的速度要快于度指标、紧密度指标和特征向量指标；在f从0.62增大到1的过程中，根据度指标和介数指标的度量结果删除节点，S下降的速度基本相同，且均快于紧密度指标和特征向量指标。这说明在对作战体系中节点重要性进行度量时，介数指标的有效性要好于度指标、紧密度指标和特征向量指标。

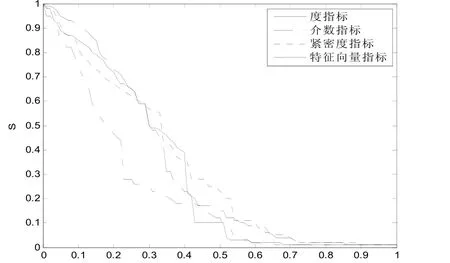
图2 S随 ff的变化情况

作战体系受到攻击的初期，最大连通分支的大小相比整个作战体系节点数目来说较大，攻击发生后去掉了一些关键节点导致某些关键路径也从作战体系中去掉，影响了节点间通信的平均路径长度，确切说是增大了平均路径长度；然而随着攻击的增加，最大连通分支越来越小，即作战体系被分成了许多独立的小的连通分支，而这时最大连通分支的平均路径长度会变小。因此。可以从 f增大时，L增大和下降的速度说明重要性指标的有效性。从图3（a）、（b）可以看出，在 f从0增大到0.04的过程中，根据度指标、介数指标、紧密度指标和特征向量指标的度量结果删除节点，L增大的速度基本相同；在f从0.04增大到1的过程中，根据介数指标的度量结果删除节点，L开始减小，而根据度指标、紧密度指标和特征向量指标的度量结果删除节点，L继续以基本相同的速度增大，分别在f等于0.40、0.33和0.32时开始下降。根据介数指标的度量结果删除节点，L不仅开始减小的时间要早于其他指标，而且减小的速度也快于其他指标。同样说明在对作战体系中节点重要性进行度量时，介数指标的有效性要好于度指标、紧密度指标和特征向量指标。

4 结束语

根据作战体系最大连通分支的大小和平均路径长度随删除节点比例的变化情况仿真分析的结果表明，在对作战体系中节点重要性进行度量时，介数指标的有效性要好于度指标、紧密度指标和特征向量指标。利用这一指标，可以准确、快速地判断作战体系中的关键节点，既可以对敌方作战体系实施精确打击，破坏其作战效能的生成和聚合，从整体上使其快速瘫痪；又可以在面临敌方精确打击时，对己方作战体系中的关键节点进行重点防护，保证其作战能力的有效发挥，达成“消灭敌人，保存自己”的目的。

[1]National Research Council. Network Science[M].The National Academies,2005.

[2]严正峰. 海军战役作战体系研究[D].南京:海军指挥学院,2007.

[3]汪小帆,等. 复杂网络理论及其应用[M].北京:清华大学出版社,2006.

[4]王林,张婧婧. 复杂网络的中心化[J].复杂系统与复杂性科学,2006(3):13-20.

[5]Albert R, Jeong H, Barabási A L. Attack and error tolerance in complex networks[J].Nature,2000,406: 387-482.