一种GPS定向滤波算法及其数据分析
黄 胜,王嘉苏
(1.青岛杰瑞自动化有限公司,山东 青岛 266071;2.中国船舶重工集团公司江苏自动化研究所,江苏 连云港 222006)
在 GPS短基线定向中,天线之间的距离都比较短,而且长度固定,因此,模糊度的固定大多采用附有已知基线长约束的OTF方法。该方法将基线长度作为一虚拟观测值与伪距相位观测值进行联合建模,利用LAMBDA方法初步求解整周模糊度的备选值,利用基线长度约束模糊度[1-4]。唐卫明博士等在文献[5]中采用基线长度约束的方法辅助确定整周模糊度,并利用单频静态数据动态单历元解算,得到了 85~95%的解算成功率。由于单频接收机价格便宜,单频单历元模糊度解算方法具有巨大的应用价值。
但在基线约束算法中,我们发现,存在一部分解满足基线约束,并通过模糊度检验,但其模糊度解算是错误的,即模糊度的解算不可靠,导致定向结果与真值偏差很大。通过实测数据分析,这部分解占总历元数的比率为1~2.5%左右,这部分解的存在影响了该算法的可靠性与稳健性。本文在基线约束算法的基础上提出一种动态准实时滤波算法,将上文所提及的错误解的比率降低了0.5~2%,提高了基线约束算法的稳健性。
1 平滑滤波模型
在实际工程中,有很大一部分是静态或低动态事后或准实时(延后数秒)应用,如流动导弹发射平台,往往有一段相对的静态观测时间。此时可以利用单历元定向方法的平滑滤波来提高解算的正确率。刘根友研究员在文献[6]中提出在静态定向中使用“加权平均”的方法,使得GPS单历元定向方法的用途更加广泛。本文基于基线载体的动态特性,在认真研究动静态数据的内在联系的基础上,提出一种动态静态均适合的平滑模型,这里称其为求差法。求差法认为:载体运动方向一般会规则变化,如果计算出来的载体运动方向发生剧变,则认为是模糊度求解错误。因此,求差法不适用于高旋转运动的载体,且载体方位角变化越规则,则平滑精度越高。
该模型有两个参数,一是平滑周期 P,二是阈值T。P是每次进行平滑处理的数据个数,亦是数据输出延后的时间,当载体运动方向变化很不规则时,P值可设为0,此时,对定向结果不作平滑处理;而T则描述了载体的动态特性,它可以理解为一秒内载体运动方向变化的限值,载体运动方向变化越快,阈值设定应该愈大。
其计算步骤如下:
a)按照基线约束模型计算出P个方位角;
b)按时间顺序计算这 P个方位角两两之间的差值;
c)如果差值大于阈值T,则认为该方位角错误,并记录该处位置,直至这P个数据处理完成。将相邻两次出现差值大于阈值之间的方位角数据记为一组,存储于二维数组B中;
d)统计 B中方位角数据最多的一组 C,并认为该组数据为正确的;
e)根据C计算出现错误历元数据组的方位角值,如果错误数据前后两组数据与C组值差值在某一限值t以内,则对该组数据进行插值修正;
求差法的关键在于第e步,一方面要求计算出错误历元的正确值,另一方面又不能对计算正确历元进行修改乃至错误,这可以通过对限值t的设定来实现。
2 试验及数据分析
为了验证本文所提算法,利用 VC6设计了 GPS单历元动态定向软件,并进行了三次试验,统计每次试验的定向成功解算率(模糊度解算成功,通过模糊度检验及基线检验)和定向正确解算率(模糊度解算成功且正确,从而定向结果正确),其中,

三次试验均采用JAVAD JNS100接收机,采样率均为1s,基线长为2.56m,截止高度角为15°。对于试验 1与试验 2,分别采用两种解算方式,解算方式1的平滑周期为0,阈值为0,即为实时动态单历元解算;解算方式2采用求差法平滑,其平滑周期为10s,阀值为10°。而试验3则分别解算三次,解算方式1为实时动态单历元解算;解算方式2、3均采用求差法平滑,其平滑周期和阈值分别为10s、20°和 30s、5°。

图1 试验2载体运动轨迹(单位为m)
第一组数据为静态定向测试,观测地点为青岛市某地,观测时间为2008年8月24日,共观测了20min左右,观测条件良好,略有遮挡。第二组数据为微动态定向测试,观测地点为青岛市崂山某湖泊中,天线固定在离水面约0.5m高的载体上,观测时间为2007年11月21日,共观测了4个小时,其载体运动轨迹见图 1。观测条件优异,周围无遮挡物。第三组数据为动态定向测试,观测地点为青岛市,天线固定在客车顶上,观测时间为2008年8月26日,共观测了60min左右。观测条件一般,公路沿线时有遮挡。其客车运行轨迹见图2。
在静态数据单历元解算时,基线的姿态可以事先精确测定,因而可以方便地求解模糊度的成功率和正确率;然而在动态试验中,只能准确地计算出成功解算率(即通过模糊度检验及基线长度约束),而很难精确判断方位角求解是否正确。在试验2中,由于载体是低动态运动,方位的变化平缓,因而可以通过这一特性,将方位角发生突变的历元认为是解算错误的。而在试验3中,由于载体运动速度较快,甚至有时会出现急转弯的地方,此时再利用试验2的判断方法则是非常近似的,此时,我们通过解算出来的方位角变化图来对比其解算效果。

图2 客车运行轨迹(单位为m,*表示10的幂)
由表1可以看出,三次试验中,试验2的观测条件最为优异,无论是实时动态解算还是求差法平滑,其成功率均很高。但在实时动态算法中,有大约2.3%历元解算方位角错误,但其模糊度通过模糊度检验,满足基线约束条件,在求差法中,通过平滑手段可将这部分历元检测出来并加以修正,从而提高了定向的正确率。试验1为静态观测,观测条件差于试验2,其解算成功率要低于试验 2;但由于其是静态观测,基线方位没有变化,从而求差法平滑的效果比较明显,能够将其正确率提高5%左右。

表1 试验数据计算结果
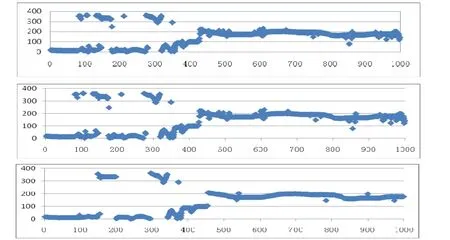
图3 试验3三种解算方式解算方位角对比
试验3的三种解算方式的计算结果见图3。由图3可以看出,当平滑周期越长,方位阈值越低,其平滑效果越好,但这种平滑结果是近似的,如果事先已经预知载体的运动方向变化不太剧烈,则可以通过增大平滑周期,缩短方位阈值的方法来提高平滑效果。反之,如果预知载体运动方向变化剧烈,则可通过相反的措施来使平滑结果能够尽可能地反映载体的真实运动状态。
3 结束语
求差法平滑实质上是对解算出来的方位角进行优化处理,适用于准实时应用环境,它根据载体的运动状态,判断并剔除解算错误的值,并在解算错误或解算失败的历元进行插值。该算法是模糊度可靠性数理统计判断方法的补充,能将GPS短基线定向成功率提高 1~5%左右,在一定程度上提高了基线约束算法在准实时低旋转变化环境下的成功率及稳健性,是一种行之有效的近似处理方法,使得GPS单频单历元定向的用途更为广泛。
[1]Teunissen P J G. Least2squares Estimation of the Integer GPS Ambiguities. 1993 IAG General Meeting, Beijing,1993.
[2]Liu G Y, Zhu Y Z, Zhu C L. Damped LAMBDA Algorithm for Single Epoch GPS Positioning. 2002 International Symposium on GPS/ GNSS , Wuhan , 2002
[3]刘万科. 附有距离约束的 GPS快速静态定位定向算法研究及程序实现[D]. 武汉:武汉大学,2004.
[4]周扬眉,刘经南,高振东. 整周模糊度整数变换前后LAMBDA方法的执行结果比较[J].全球定位系统,2004(2).
[5]唐卫明,孙红星,刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J].武汉大学学报(信息科学版)2005(5).
[6]刘根友,欧吉坤. GPS单历元定向和测姿算法及其精度分析[J].武汉大学学报(信息科学版)2003(12).
[7]韩保民, 欧吉坤. 一种附有约束的单频单历元 GPS双差相位解算方法[J].测绘学报,2003,31(4).

