基于Copula的商业银行信用—汇率风险整合的实证研究

王宗润 肖红艳 周艳菊

一 、引言

对多种风险进行综合的度量和管理是现代银行业全面风险管理的重要内容，然而风险的交叉作用和异质性特征给风险的全面量化管理带来困难，通过引入Copula函数度量商业银行的整合风险的方法就应运而生了。Copula是连接多元分布函数和单变量边缘分布函数的函数，它的出现不仅将风险分析和多变量时间序列分析推向了一个新阶段，而且使得金融风险度量方法有了新的突破，即Copula可测度非椭球分布形分布(有极端事件函数的分布)的风险，也可以准确地描述多变量分布的相关性。Copula函数运用于整合风险度量有两个优势：1）利用连接函数能够有效地解决整合风险管理中不同类型风险的联合分布建模;2)利用连接函数方法更容易通过Monte-Carlo模拟方法计算整合收益率的VaR;和CVaR值。

Embrechts（1999）首次将 Copula理论引入金融领域，探讨了在金融市场中采用线性相关指标度量相依性的局限性，建议采用Copula来估计随机变量间的联合分布，在研究思想上对Copula的应用前景做了很好的展望；Nelson（1999）系统总结了这一起先源于统计学而后被逐渐应用于金融风险管理领域的主要研究成果，包括Copula的基本性质，Copula在相关性研究、风险测度以及多变量联合分布构建中的应用等。Bouye（2000）探讨了Copula函数在资产组合市场风险、信用风险、操作风险以及极端情况中的应用。Kuritzkes等（2003）在联合分布服从正态分布的一系列假设下，对整体风险进行研究表明其较之边缘分布的简单加总有明显的差异。Rosenberg J.V.等（2006）使用正态Copula和Student t copula对商业银行的三种风险（信用风险、市场风险和操作风险）进行了整合，并对美国商业银行的整体风险水平进行了度量。在国内，张尧庭（2002）最早介绍Copula方法，并说明了Copula函数能够描述金融变量之间的相依关系。张明恒（2004）研究了多金融资产风险价值的Copula计量模型和计算方法。吴振翔等（2006）使用Copula-GARCH模型对投资组合的风险进行分析。李平、马婷婷(2008)采用Clayton Copula函数对商业银行市场风险和信用风险进行整合，然后根据投资组合VaR的计算方法，再与操作风险进行整合，得到三种风险的整体VaR。侯成琪、王频（2008） 比较分析了 Copula-VaR与 Hybrid-VaR、Normal-VaR和Additive-VaR等几种常用的风险度量方法后发现，Normal-VaR和Additive-VaR存在高估风险的倾向，而Copula-VaR能够有效解决集成风险管理中联合损失分布函数的构建问题并能通过蒙特卡洛模拟较为便捷的计算整合收益率的VaR值。余孝军（2009）选取易于计算的椭球族Copula结合不同的边缘分布假设来构建10支银行股票构成的组合的联合分布，计算出对应的VaR和CVaR。众多学者对Copula函数进行了广泛的探索，其应用已经涵盖了相关性分析、期权定价、投资组合管理、风险管理等众多领域，其中在风险管理中的应用尤为广泛，分别在VaR方法、极值理论、时间序列分析、信用风险分析、银行整体风险分析中取得了长足的发展。

以上的研究对应用Copula函数度量整合风险做出了有益的探索，但是整合风险的类型有局限。刘京军 首次利用期权方法研究了汇率风险和信用风险的相关性，表明信用利差是汇率波动率的增函数，汇率初始值的减函数，研究发现：通过模拟分析和实证分析汇率变化对信用利差和违约概率的影响得出结论：汇率波动不仅仅使企业的融资成本增加，而且商业银行可能面临因汇率变化导致信用风险问题，遗憾的是，他并未对两类风险的量化与集成展开深入研究。另一方面，长期以来，银行都是将信用与汇率风险单独加以控制和管理，然而大量的实践表明信用风险和汇率风险常常是夹杂在一起共同影响银行经营的。

从Copula的实际运用来看，关键是要寻找一个恰当的分布来拟合样本数据的边际分布，对于如何确定边际分布的类型，不少文献的研究通常是在边际分布服从一系列的理论分布的前提下进行的。在运用Copula函数对风险进行整合的过程中，边缘分布的估计是至关重要的一步，它是正确的选择Copula函数，对风险进行正确整合的前提。因此，本文主要从实际运用的角度出发，以更符合实际的经验累积分布拟合三家银行信用风险和汇率风险的边缘分布，在不同族类、不同种类Copula函数中选优对深圳发展银行、上海浦东发展银行、中国民生银行信用收益率和汇率收益率风险进行整合度量研究，求出整合风险的VaR值和CVaR值，并对三家银行的整合风险水平进行比较分析。

本文结构安排如下：第一部分介绍Copula函数的定义和性质；第二部分阐述Copula函数的参数估计方法；第三部分介绍最优Copula函数的选择方法；第四部分以深圳发展银行、上海浦东发展银行、中国民生银行为研究对象进行实证分析；第五部分是结论。

二、几种基本的Copula函数及其性质

Copula函数成员广泛，金融分析中常用的主要有两大类，下面以二维情况为例，对它们分别进行介绍：

1.两类Copula函数族

（1）Elliptical Copula函数族

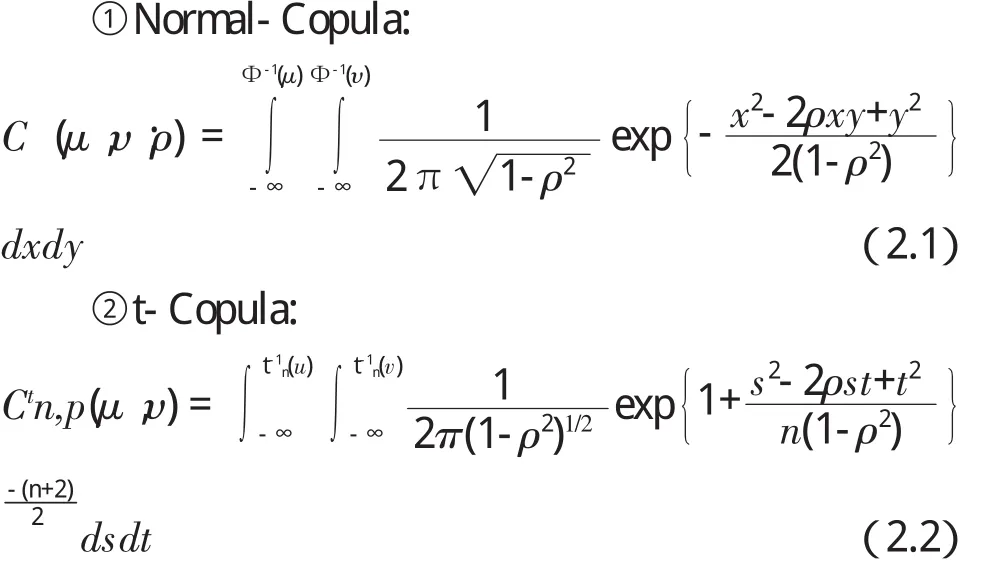
（2）Archimedean Copula函数族

2.Copula函数的特点和适用范围

上述五种Copula函数的分布特征表现出多样的形态，表1对五种Copula函数各自的特点和适用范围进行了总结。

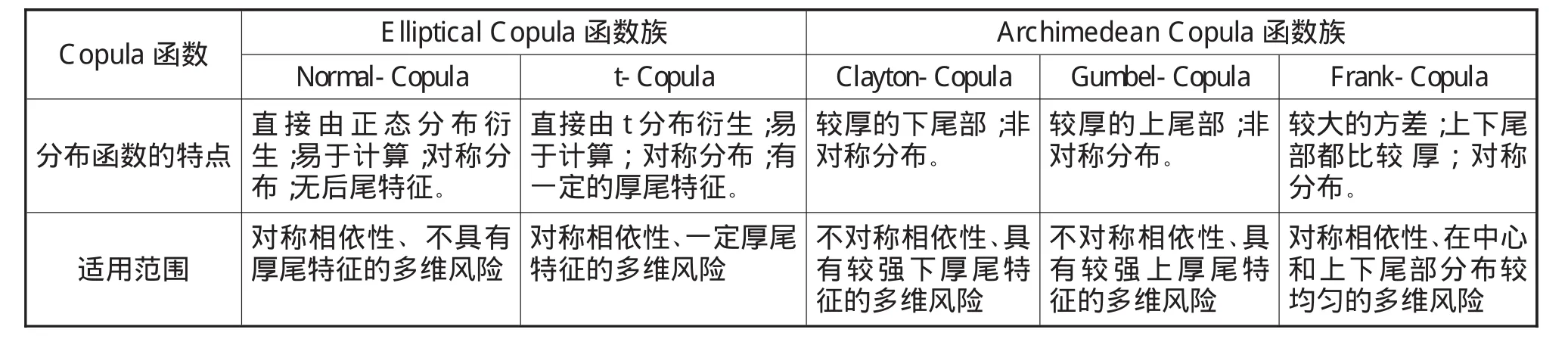
表1 Copula函数的特点和适用范围

三、Copula函数的参数估计方法

估计备选的五种不同的Copula函数参数采用不同的方法。

对于Elliptical Copula函数族中的Normal-Copula采用秩相关系数来估计参数 ，两者的关系可由ρ＝sin（π/2τ）表示。其中τ为Kendall秩相关系数。对于t-Copula函数，本文采用伪极大似然估计法，该过程该过程用Matlab 2008a软件实现。

对于Archimedean Copula函数族中的参数估计，根据秩相关系数来估计。

表2 Archimedean Copulas的一些相关性测度

分析表2，由于某些Copula函数的Spearman’ρ没有具体的表达形式，我们采用Kendall’τ来估计其参数。

四、最优Copula函数的选择方法及相应的风险测度指标

通过比较判断不同族类、不同种类Copula函数与经验Copula函数之间的拟合优度。对于拟合优度的判断方法，采用图像法，图像法主要通过QQ图（分位数图）来观察通过不同Copula函数得出的分布值与经验Copula函数的距离，如果两者的拟合程度较高，则QQ图上两者都将重合于45°直线上，如果无法精确细致地观察多种Copula函数拟合结果的差别，我们采用Kolmogorov-Smirnov（K-S）检验来计算估计的Copula函数与经验分布函数之间的最大距离，从而计算出相应的P值，P值越大拟合的效果就越好。

五、实证分析

1.数据选取

信用风险产生于资金的提供者及使用者的已签合约或者是一种或有合约的交易过程中，是金融市场上最为古老、最为基本的一类风险。它是指在金融交易中交易对手违约或信用品质潜在变化而导致发生损失的可能性。对于信用风险的度量，国内的相关研究多是从上市公司角度进行的财务预警研究。虽然 KMV模型相对于我国目前商业银行信用风险度量技术具有较大的优越性，但该模型对资产收益的正态性假设与我国证券市场资产价格的非正态性之间存在矛盾，并且在我国完全应用KMV模型还存在一定的困难，如历史违约数据缺乏、数据失信，在有关公司的历史违约数据严重缺乏时，我们很难把DD（违约距离）转换成DF(违约概率)。由于资料的可获得性差，并考虑到银行面临的信用风险主要来自贷款业务，所以在进行信用风险度量时，本文借鉴侯成琪、王频（2008）的做法，以2003年第一季度到2009年第三季度的深圳发展银行、上海浦东发展银行、中国民生银行财务报表中的数据为原始数据，将利润表中的“利息收入”除以资产负债表中“贷款总额”得到与信用风险相关的业务的收益率即信用收益率 。由于风险整合时的交易数据需相匹配，所以采用最具有代表性的人民币对美元汇率，选取的时间段为2003年第一季度到2009年第三季度，将每个季度最后一天的汇率作为整个季度的汇率的中间价。

2.数据的正态分布检验

因篇幅所限，本文仅列出深圳发展银行信用收益率和汇率收益率的正态分布拟合图，如图1、图2所示。

图1 信用收益率的正态分布拟合图

图2 汇率收益率的正态分布拟合图

从上图可以看出：样本数据均不服从正态分布。

3.整合风险的度量

在运用Copula函数对风险进行整合的过程中，边缘分布的估计是至关重要的，它是正确选择Copula函数并实施风险整合的前提。以往文献常用Beta分布和t分布来拟合信用收益率，但单样本的Kolmogorov-Smirnov检验表明，其并不服从Beta分布和t分布。鉴于此，本文直接采用能更好拟合实际分布的经验累积分布来拟合三家银行的信用收益率及汇率收益率边缘分布。

边缘分布函数确定以后，我们采用文中第二部分介绍的参数估计方法求得各种Copula函数的参数，见表3。

我们用QQ分位数图3（以深圳发展银行为例）来考察拟合程度：

图3 五种Copula函数和经验Copula的QQ分位数图

从图3可以看出，Elliptical Copula函数族对样本数据的拟合程度欠佳，而Archimedean Copula函数族对数据的拟合程度较高，所以本文采用Gumbel Copula函数对深圳发展银行的信用－汇率风险进行整合。

表3 各种的Copula函数的参数值

由于QQ分位数图对深圳发展银行的拟合程度考察差别不明显，所以上海浦东发展银行和中国民生银行本文采用K-S检验的方法对几种Copula函数的拟合程度进行考察，结果如表4所示。

表4 各种的Copula函数的参数值

对表4中K-S检验的P值进行分析可知，用Gumbel Copula函数来拟合浦发银行的收益率序列、用Clayton Copula来拟合民生银行的收益率序列能得到较为精确地结果，因为在这两种情况的P值都能超过相应的置信水平（0.1，0.05，0.01），并且P值都非常大。利用蒙特卡洛模拟计算产生相应的VaR值和CVaR值。具体的过程如下：

（1）生成服从[0，1]上均匀分布的随机数μ；

（2）生成分布函数为信用收益率的条件边际连接函数的随机数 ，这样可以保证两组随机数之间的相关结构可以用Copula函数来描述；

（3）对随机数μ进行函数变换，得到边际分布为信用收益率边际分布的随机数；

（4）对随机数ν进行函数变换，得到边际分布为汇率日对数收益率边际分布的随机数；

（5）通过r=0.5μ+0.5ν得到整合收益率的随机数；

（6）计算整合收益率的VaR值和CVaR值。

通过分别模拟500、1000、5000次，发现当模拟次数为5000时，计算的VaR和CVaR值较收敛，

按照以上步骤，我们计算出不同置信度（0.01,0.05,0.1）下Copula函数的风险值，结果如表5所示。

表5 三家银行信用-汇率风险的VaR值和CVaR值

分析表5中的数据，有如下结果：

1）三家银行的风险水平都不是很大，例如深圳发展银行在置信度为99%的情况下的信用收益率和汇率收益率的整合风险水平为0.1073%，其期望损失为0.1639%。

2）对三家银行的风险水平进行比较，可知深圳发展银行的风险水平稍大，浦东发展银行的次之，中国民生银行的风险水平相对较小，但三者之间的差别并不大。

3）以整合的结果作为指导，引导决策者考虑信用风险和汇率风险的相关性，可以避免存在过多的风险准备金，提高资金的利用率，使银行获得更大的收益。

六、结论

本文对深圳发展银行、上海浦东发展银行、中国民生银行的信用-汇率风险进行了度量，在考虑信用风险和汇率风险相关性的基础上，采用能更好拟合实际数据的经验累积分布函数对边缘分布进行拟合，通过选取最优Copula函数对两者的整合风险进行度量，得到了信用-汇率风险的VaR值和CVaR值，并对三家银行的风险水平进行了比较，发现深圳发展银行的风险水平稍大，浦东发展银行的次之，中国民生银行的风险水平相对较小，但三者之间的差别并不大。决策者可以根据整合的结果在整体层面上掌握风险水平，决定信用-汇率风险的风险资本，在有效避免存在过多准备金的同时，又防止了因准备金不足带来的损失,有利于风险监管者对整合风险进行分散和监管。

［1］Embrechets p.,Mcneil A.J.,Straumann D..Correlations:pitfalls and alternatives[J].Risk,1999,12:69-71.

［2］Nelson.R.B.An introduction to Copulas[M].Springer.New York,1999

［3］Bouye,E.,V.duurrleman,A.Nikeghbali,G.riboulet and T.Roncalli.Copulas for finance a reading guide and some applications.Working paper,Credit Lyonnais,2000

［4］Kuritkes A.Schuermann T.Weiner S.W.risk management and capital adequacy of financial conglomerates[J].Risk measurement,Papers in Financial Services,2003,141-194

［5］Rosenberg Johua V.,Til Schuermann.Ageneral approach to integrated risk management with skewed,fat-tailed risks[J].Journal of Financial Economics.2006(79):569-614

［6］张尧庭.连接函数copula技术与金融风险分析[J]:统计研究.2002(4):48-51

［7］张尧庭.我们应该选用什么样的相关性指标[J].统计研究.2002(9):41-44

［8］张明恒.多金融资产风险价值的Copula计量方法研究[J].数量经济技术经济研究.2004，(4)，67-70

［9］吴振翔，陈敏，叶五一，等.基于Copula-Garch的投资组合风险分析[J].系统工程理论与实践,2006,26(3):45-52

［10］李平，马婷婷.基于Copula的我国商业银行整体风险度量.[J].管理科学.2008(6)

［11］侯成琪,王频.基于连接函数的整合风险度量研究[J].统计研究.2008(11),72-80

［12］余孝军.Copula理论在商业银行风险管理中的应用[J].贵州财经学院学报.2009(1),64-68