应用时间精确自由尾迹方法的桨叶总距突增响应特性分析

王国才，李春华，陈平剑，赵小全

（1.海军驻景德镇地区军事代表室；2.中国直升机设计研究所，江西 景德镇 333001；3.总参谋部陆航部驻景德镇地区军事代表室，江西 景德镇 333002）

直升机依靠旋翼来产生升力和操纵力，因此旋翼对操纵输入的动态响应特性在很大程度上决定了直升机的飞行性能[1]。许多机动飞行科目，如垂直跃上/跃下、快速侧移等，其操纵输入是阶跃式的快速输入，会导致旋翼拉力、诱导速度、挥舞角等气动参数和旋翼性能出现动态的非定常变化，尤其是关键的总距输入改变会对旋翼的操纵性能有较大的影响。因此，开展旋翼桨叶在总距突增时的气动响应特性分析具有重要的理论和实际意义[2]。

桨叶的气动响应与旋翼入流分布密切相关，目前旋翼入流的求解方法主要有动量理论、广义动态入流理论、涡流理论方法和CFD方法等。动量理论只给出了最简单的均匀诱导速度分布，不适合于桨叶气动载荷及动态响应特性计算。广义动态入流理论是20世纪80年代由Peters、He等人[3]发展起来的旋翼入流计算方法，该方法有较好的精度，但难以准确模拟旋翼尾迹畸变对入流分布的瞬时影响。而CFD方法分析操纵响应在目前还不成熟。涡流理论方法[4-5]，尤其是基于自由尾迹的涡方法计入了尾迹的收缩和涡线的畸变，允许涡线自由移动，考虑了尾迹自诱导作用，可以更好地模拟实际尾迹形状及入流变化，目前广泛用于模拟桨叶尾迹和分析旋翼入流特性，具有快捷高效、计算精度高的优点。而且，近年来Leishman[6]等人开始提出了一种时间精确的自由尾迹分析模型，该模型利用随时间变化的尾迹迭代算法，精确预测尾迹的瞬时变化过程，能够较好地计算各时间点旋翼入流的非定常影响。国内对时间精确自由尾迹计算方法的研究很少，而关于自由尾迹方法对旋翼桨叶动态响应特性的研究目前还未见相关的文献发表。

本文在课题组已有的旋翼准定常松弛尾迹研究的基础[7]上，通过建立随时间变化的旋翼自由尾迹模型、桨叶气动模型及动力学模型和非定常翼型模型，并结合旋翼配平模型，尝试建立一种新的时间精确自由尾迹计算方法。并以该方法分析桨叶在总距突增时，旋翼的力和力矩系数非定常变化的时间历程，以及桨叶的动态挥舞响应特性。

1 计算模型

1.1 尾迹模型

随着旋翼旋转，桨叶后缘脱出螺旋形尾迹，且无论在悬停还是前飞，各片桨叶的尾迹涡均交织在一起[5]。因此，要利用B-S定理来预测旋翼附近的诱导速度，需先计算尾迹涡线的几何形状。

旋翼涡线以当地速度（含自由流速度和旋翼诱导速度 vind）自由运动，尾迹涡线的控制方程[7]可描述为：

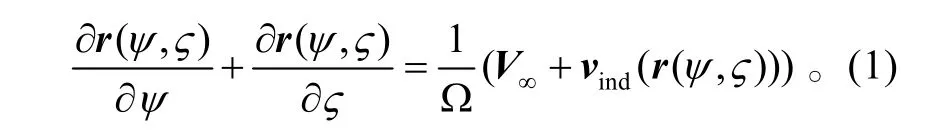
对于尾迹的离散采用PC2B方法[6]，即用一个二阶向后差分方法将网格[ψ,ψ+Δψ]×[ς,ς+Δς]中心点(ψ+Δψ/2,ς+Δς/2)的差分表达式近似代替控制方程中的偏微分项，计算点与周围节点的依赖关系如图1所示。

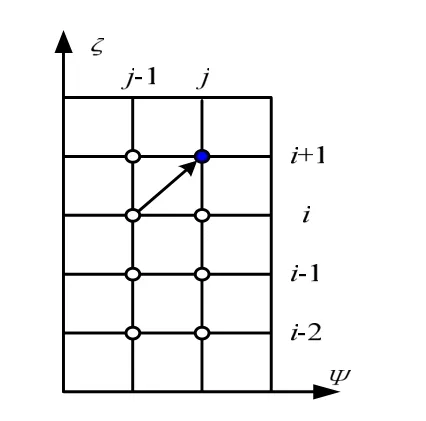
图1 尾迹离散点的计算示意图

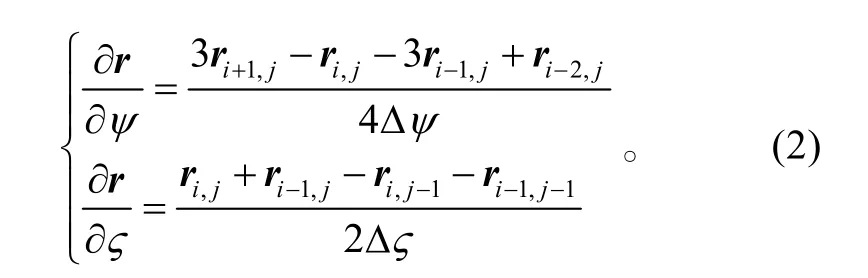
利用上述有限差分格式，尾迹控制方程离散为：

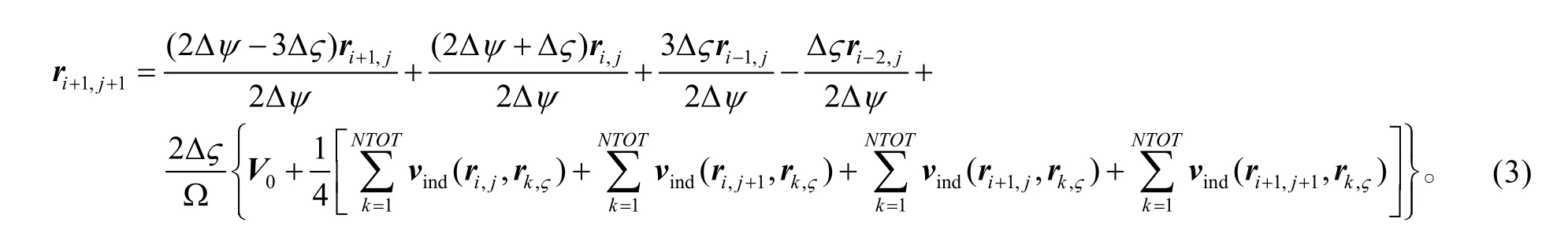
1.2 桨叶模型

本文桨叶模型采用Weissinger-L 简单升力面模型[6-7]，该模型对桨叶以定环量的涡段来模拟，即沿桨叶展向分成若干小段，每一小段中附着涡位于1/4弦线，环量Γ为常数，相同数目的控制点布置在3/4弦线中点处。由于载荷沿桨叶展向变化，不同强度的涡从桨叶后缘拖出，构成旋翼的尾迹。

旋翼尾迹分为近尾迹和远尾迹，近尾迹由沿每片桨叶后缘脱出的自由尾随涡和脱体涡构成桨叶涡面，其各段涡线的强度为桨叶相邻两展向微段的附着环量之差，而每段涡线环量的弦向变化形成脱体涡。沿桨叶后缘脱出的尾迹在转过一定角度后聚合并卷起为桨尖涡线，构成远尾迹。

Weissinger-L 气动模型的难点在于计算各涡线段的环量值。本文采用边界条件即控制点的法向诱导速度为零来进行求解，如式(4)：

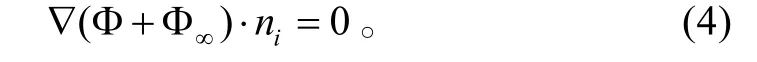
为了求解方程(4)，需先求出影响系数，对于任意控制点I，影响系数I(u,v,w)ij是指所有涡线，环量为1时对控制点的诱导速度，在获得影响系数后，边界条件(4)可表示为：

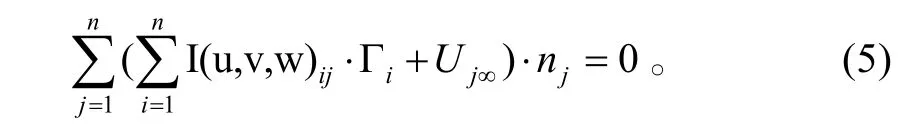
由于涡线位置难以确定，因此气动模型中对环量的求解需结合1.1的自由尾迹模型。

桨叶的挥舞动力方程通过离心力矩、惯性力矩、气动力矩、弹簧力矩的平衡来建立，方程如下：

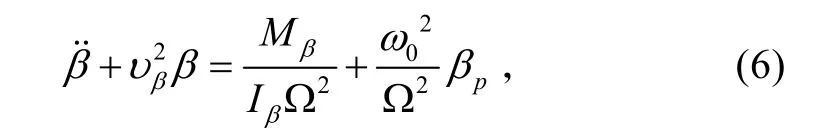
1.3 非定常翼型模型

要准确计算桨叶的拉力，需获得详细的翼型升、阻特性参数。而对于大多数翼型而言，该参数难以获得。为此，本文采用了Beddoes 翼型模型[8]计算翼型的升、阻特性。其迎角表示的翼型升力系数计算公式为：

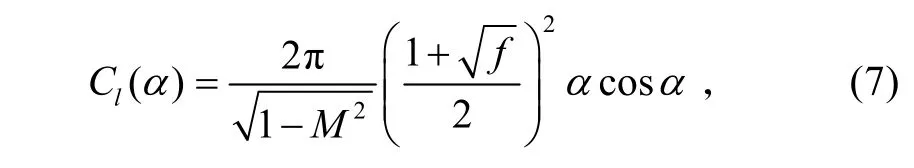
式中：M为马赫数。

对式中的f，Beddoes 提出的一个经验表达式[8]：

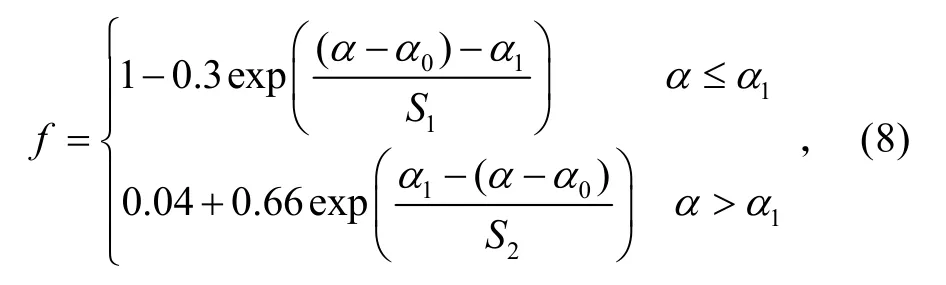
式中：0α为翼型的零升迎角；1α为气流分离点为0.7时失速角；而1S和S2定义了翼型的静态失速特性。1α、1S和S2的数值可表示成马赫数M的指数关系式，具体取值参见文献[8]。

翼型的阻力系数表示为：

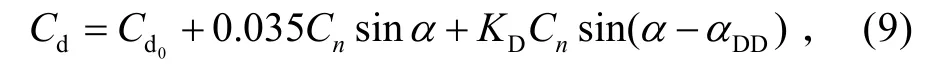
式中：

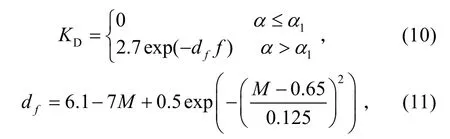
Cd0为零升阻力系数，αDD为阻力发散角，也可分别表示成马赫数M的指数关系式[8]。

1.4 配平模型

利用式(6)获得了桨叶挥舞角后，需要进一步求出旋翼的总距和周期变距[5]。计算思路为：固定旋翼的轴倾角和前飞速度，调整旋翼总距角 θ0.7和周期变距角 θ1c、θ1s以满足给定的旋翼拉力系数CT和桨盘后倒角 a1、侧倾角 b1。

平衡求解通过将非线性输出矢量对操纵矢量进行泰勒级数展开至一阶并化简得：

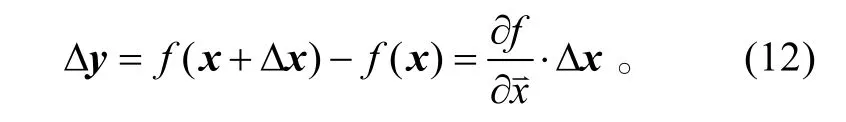
于是输入和输出之间存在如下关系：

式中，J为雅可比矩阵，定义为：

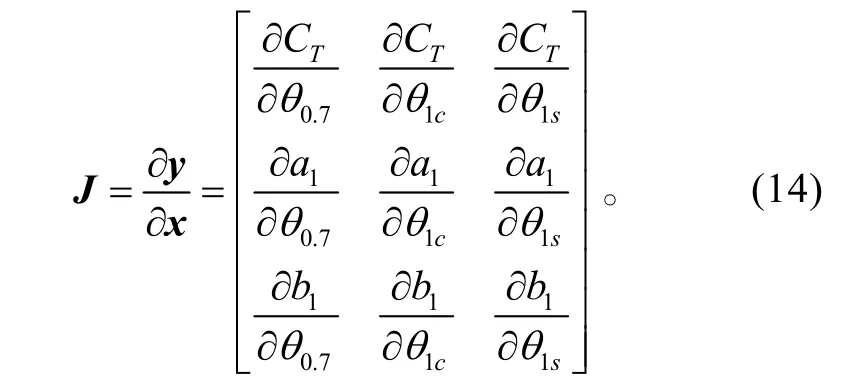
在求解过程中，初始值不一定在真实解附近，为保证稳定性，引入一阻尼因子λ（0＜λ≤1.0）

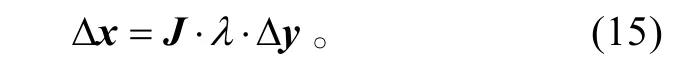
当满足 Δ x＜RMS（RMS为指定小量）时，认为获得收敛的配平操纵量。

2 计算步骤

利用上节给出的各分析模型，本文建立了新的时间精确自由尾迹方法，其分析旋翼气动响应特性的计算步骤为：

步骤一，给出飞行条件、旋翼参数，计算旋翼平均入流和尾迹初始位置；

步骤二，沿方位角步进，迭代计算出定常飞行条件的尾迹几何形状，并完成配平分析；

步骤三，对旋翼的总距操纵输入做突增改变；

步骤四，方位角步进，计算尾迹节点的诱导速度，使用PC2B算法更新尾迹的几何形状；

步骤五，计算桨叶的环量和气动力变化，分析桨叶的挥舞响应特性，返回步骤四，计算下一个时间步的尾迹形状和动态响应特性，直到各气动响应值达到相对稳定。

3 验证算例

旋翼入流计算的准确性是载荷响应和挥舞响应计算的关键。因此，利用本文的方法首先计算了旋翼入流，来验证方法的正确性。以马里兰大学的2MRTS 旋翼[9]为算例，图2计算了模型旋翼在0.15和0.3 前进比的旋翼纵向入流分布，图中横坐标表示桨盘纵向位置（来流方向）与旋翼半径的比值。可以看出，入流分布为典型前大后小，入流梯度与前进比有关，计算结果与实验值[9]吻合较好。

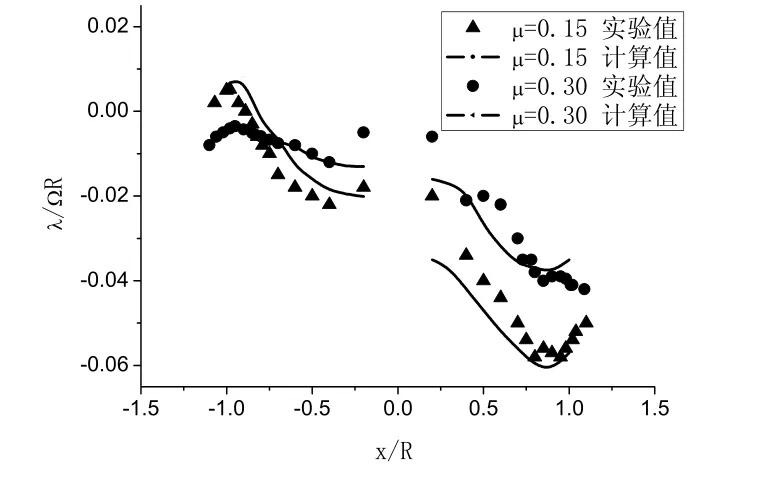
图2 前飞时旋翼纵向入流的计算值与实验值对比

图3以全尺寸直升机旋翼[10]为算例，计算了悬停时桨叶总距以200 (°)/s的速度增加到12°，之后保持总距不变时，旋翼拉力系数变化的时间历程，图中横坐标表示方位角的变化。可以看出悬停时的桨叶的拉力没有周期性变化，拉力系数迅速增大且有过冲，然后降低并在一周以后逐步达到稳定状态，计算结果与实验结果[10]吻合较好。

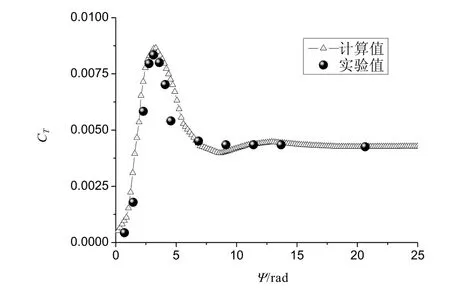
图3 悬停时计算的旋翼拉力系数响应与实验值对比

通过对入流和总距增加时拉力系数响应曲线的实验值与计算值对比，可以知道本文的方法有较好的准确性，可用来进行旋翼的响应特性分析。

4 总距突增响应分析

本节以表1的模型旋翼为算例，计算总距阶跃突增时旋翼的力、力矩系数变化及挥舞响应特性。输入条件为：旋翼稳定飞行后，旋转一周，然后总距作阶跃式突增。

表1 模型旋翼参数

4.1 悬停

拉力系数为0.01时，计算获得的悬停旋翼总距值为0.233 rad，周期变距为0。此时旋翼挥舞形成锥度角为2.78°，侧倒角和后倒角为0°。由于悬停时桨叶的气动环境相同，因而旋翼的拉力系数和锥度角均无周期性变化。图4为将桨叶总距增加到0.245 rad和0.25 rad时，其旋翼拉力系数变化的时间历程，受阶跃总距输入影响，拉力系数也近乎阶跃式突增，随着拉力系数的增大，旋翼入流也增大，于是桨叶的有效迎角又降低了。因此，拉力系数又迅速回落，之后振荡上升，经过约两个周期后，达到稳定状态。稳定后的拉力系数比总距增加前分别增加了20%和26%。

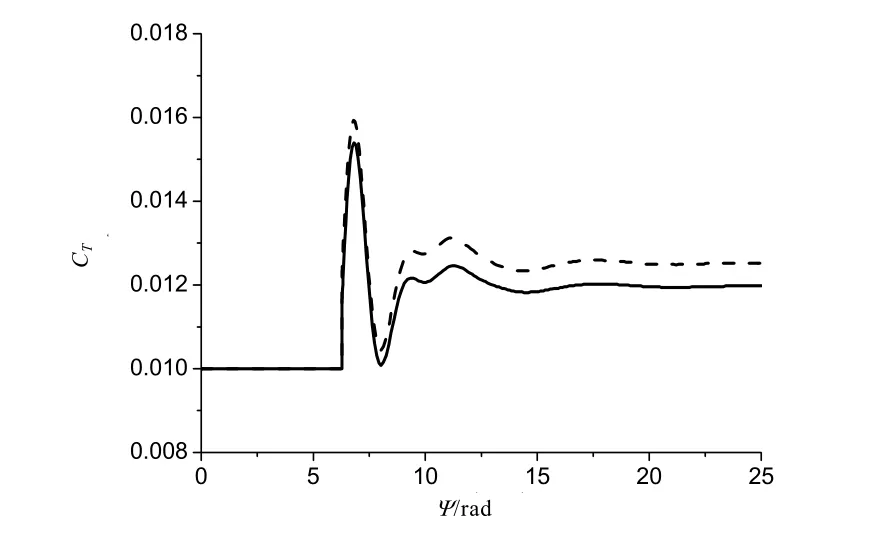
图4 总距突增时旋翼拉力系数变化的时间历程（悬停）

图5为总距增加到0.245 rad和0.25 rad时，旋翼锥度角的响应特性，初始锥度角2.78°。相比拉力系数变化趋势，总距突增后锥度角的增大较为平缓，之后呈振荡趋势，也在约两个周期后在更大的锥度角位置达到稳定，稳定后的锥度角分别为3.12°和3.27°。

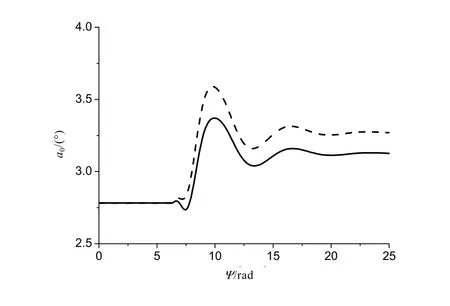
图5 总距突增时的锥度角变化的时间历程（悬停）

4.2 前飞

图6分别为前进比为0.1和0.2时的总距突增时的旋翼拉力系数响应历程。受来流影响，前飞时桨叶的气动环境有周期性变化，因此，旋翼拉力系数也呈现周期性变化。前进比为0.1和0.2，拉力系数为0.01时计算的桨叶总距分别是0.219 rad和0.204 rad。与悬停类似，总距阶跃突增到0.25 rad后，拉力系数迅速增大，然后回落，并振荡达到稳定。桨叶总距增加到0.25 rad后，前飞前进比0.2的桨叶拉力系数比0.1 大。

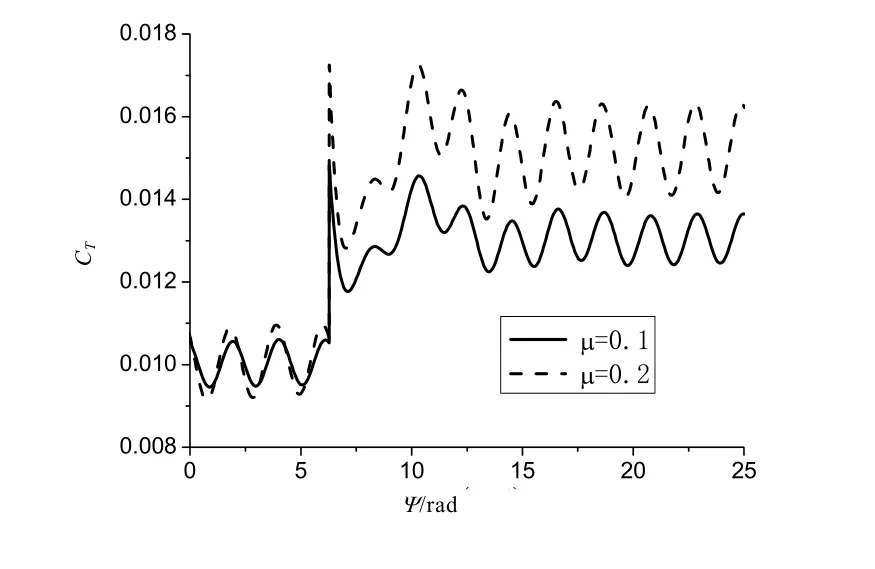
图6 总距突增时旋翼拉力系数变化的时间历程（前飞）

图7为前飞时旋翼锥度角的响应历程。总距增加前，前进比0.2时的锥度角比0.1的略大。总距突增后，锥度角较快增大且过冲回落，然后达到稳定，前飞时锥度角也呈现周期性变化，但幅度并不大。对比图5可知，相同拉力系数时，悬停时锥度角最小。前进比越大，锥度角也越大。

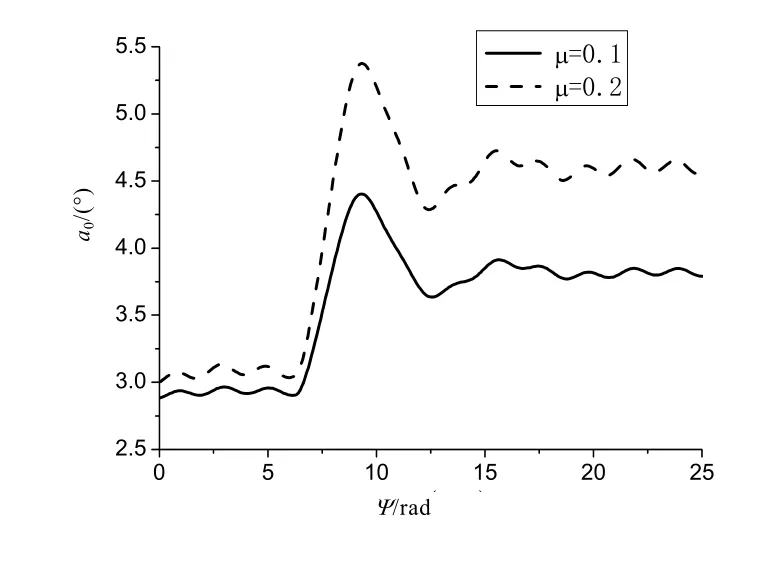
图7 总距突增时的锥度角变化的时间历程（前飞）

图8为前进比为0.1，总距突增时，俯仰和滚转力矩变化的时间历程。与拉力系数类似，前飞时受周期气动环境的影响，俯仰和滚转力矩均有周期性变化趋势。在前进比0.1时，模型旋翼的俯仰力矩和滚转力矩的峰值相位差约为32°。总距增加后，力矩系数的幅值都增加了，但俯仰力矩的均值相比总距变化前变化不明显，而滚转力矩略有增加。

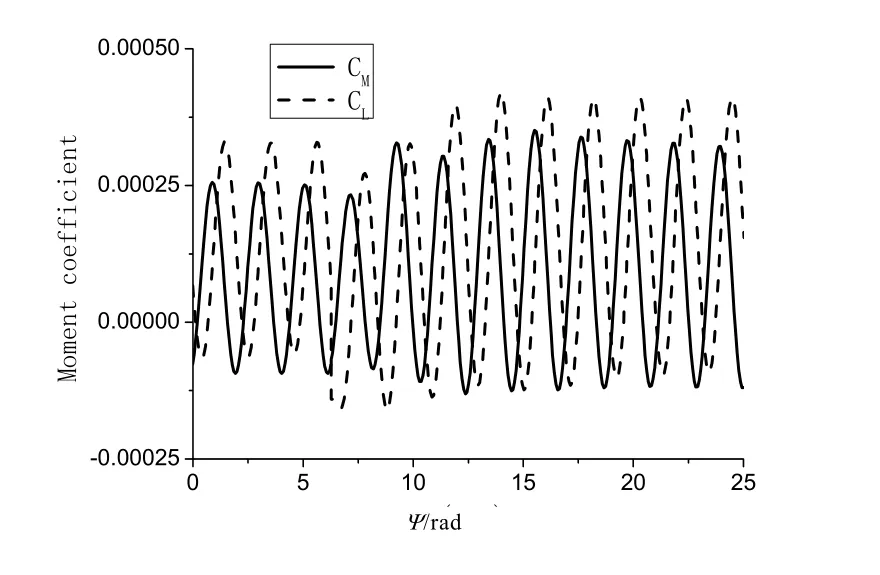
图8 总距突增时旋翼力矩系数变化的时间历程（μ=0.1）

图9为前进比为0.2，俯仰和滚转力矩变化的时间历程。

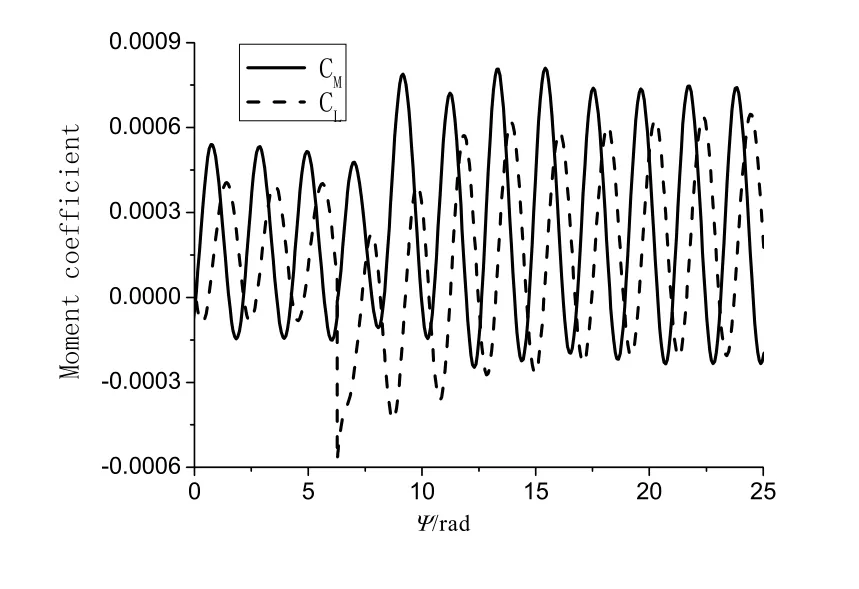
图9 总距突增时旋翼力矩系数变化的时间历程（μ=0.2）

随着前进比的增加，相同拉力系数时的俯仰和滚转力矩均有所增大。在前进比为0.2时，模型旋翼的俯仰力矩和滚转力矩的峰值相位差约为41°，比前进比为0.1时大。俯仰力矩仍然是均值基本不变，幅值增大。而滚转力矩系数是先减小后增大。在前进比为0.2时，算例计算的俯仰力矩略大于滚转力矩系数。

5 结论

1）无论是悬停还是前飞，桨叶总距的阶跃突增，会使旋翼拉力系数产生阶跃式的增大，然后迅速回落且振荡变化，约在2个周期后达到稳定。而锥度角的响应相对平滑，先增加过冲后再回落，并振荡稳定。拉力系数和锥度角的稳态值主要由旋翼总距和飞行速度决定。

2）前飞时，受周期气动环境的影响，在总距改变之前和之后，旋翼的拉力系数、俯仰力矩系数、滚转力矩系数和锥度角都有周期性变化，但锥度角的周期性变化较小。

3）锥度角与拉力系数和前进比有关。在相同拉力系数时，悬停时锥度角最小，随着前进比增大，锥度角也越大。

4）前飞时，总距突增后俯仰力矩幅值增大，均值几乎不变。而滚转力矩系数不但幅值增大，且均值也略有增加。前进比的大小会改变俯仰和滚转力矩系数峰值之间的相位差。

5）本文建立的新的时间精确自由尾迹计算方法，能够有效计算总距突增时的旋翼拉力、力矩系数和挥舞响应等旋翼的非定常气动特性。

[1]徐国华,王适存.具有后掠桨尖的旋翼气动特性计算方法[J].空气动力学学报,1999,17(3)∶111-112.

[2]PETERS D A,NINH H Q.Dynamic inflow for practical applications[J].Journal of the American Helicopter Society,1988,33(4)∶64-68.

[3]HE C J.Development and application of a generalized dynamic wake theory for lifting rotors[D].Georgia Institute of Technology,1989.

[4]MILLER W O,BLISS D B.Direct periodic solutions of rotor free wake calculations[J].Journal of the American Helicopter Society,1993,38(2)∶53-60.

[5]BAGAI A,LEISHMAN J G.Rotor free wake modeling using a pseudo implicit technique-including comparisons with experimental data[J].Journal of the American Helicopter Society,1995,40(3)∶1276-1285.

[6]BHAGWAT M J,LEISHMAN J G.Time-accurate free-vortex wake model for dynamic rotor response[C]//American Helicopter Society Specialist Meeting.2000.

[7]李春华,徐国华.悬停和前飞状态倾转旋翼机的旋翼自由尾迹计算方法[J].空气动力学学报,2005,23(2)∶152-156.

[8]BEDDOES T S.A wake model for high resolution airloads[C]//Proceedings of the 2ndInternational Conference on Basic Rotorcraft Research.1985.

[9]ELLIOT J W,ALTHOFF S L,SAILEY R H.Inflow measurements made with a laser velocimeter on a helicopter model in forward flight[R].NASA TM 100545,1988.

[10]CARPENTER P J,FRIDOVICH B.Effect of a rapid blade-pitch increase on the thrust and induced-velocity response of a full-scale helicopter rotor[R].NACA TN 3044,1953.