一种单传感器实时系统误差配准算法

宋 强，崔亚奇，何 友

（海军航空工程学院 电子信息工程系，山东 烟台 264001）

0 引言

目前，尽管多传感器信息融合技术及其理论有了飞速的发展，但是在实际的多雷达网数据处理系统中仍然有很多技术难点需要攻克，而传感器系统误差配准问题就是其中一个研究热点[1]。传感器系统误差配准的目的是准确估计并校正传感器的固有系统偏差，为其后端航迹关联与融合提供技术保障，其处理好坏将直接影响多传感器信息融合系统融合性能与可靠性[2]。

由于传感器误差配准技术均需利用各传感器对固定或运动目标的观测信息来实施。因而，按照目标的合作程度，可将当前主要的误差配准技术分为两大类，分别是基于合作式目标信息与非合作式目标信息的传感器配准技术。

对于基于合作式目标的传感器配准技术[3-7]，其前提是能够获取位置已知的固定目标或者能够实时提供高精度自身定位信息的运动目标（即合作式目标），再基于上述目标位置信息与传感器对目标量测信息构建系统误差观测模型来实施系统误差配准与补偿。采用这类技术无须多传感器协同，单部传感器自身就能达到系统误差的准确配准，但缺点是需要实时获取目标位置，并能够与传感器进行协同配准；而当无法获知目标真实位置信息时，就需要采用基于非合作式目标的配准技术[8-12]，但其前提是需要多传感器之间进行协同配准，即基于多传感器对同一运动目标的量测信息来构建对多传感器系统的观测模型，以实现对各传感器的精确误差配准。因而，该类技术的优点是无须目标自身提供定位信息，但缺点是需要多传感器进行协同配准处理，这就首先需要对目标航迹数据进行可靠关联，但此时各传感器未配准的固有系统误差又将使得航迹关联性能不可靠，导致关联与配准间产生技术矛盾的问题[13]，此外，传感器间的协同配准还将面临着异步传感器的数据时间同步问题，并且传感器间的数据通信需求还将对通信数据链造成较高的负担。

因此，为克服非合作式目标配准技术需要多部传感器相互配合进行，以及合作式目标配准技术需要目标与传感器协同处理等需求局限所带来的问题。本文研究基于非合作式固定目标的单传感器系统误差配准问题，并提出一种单传感器实时系统误差配准算法，算法利用运动平台传感器对固定目标的2时刻量测，构建系统状态方程及量测方程，通过滤波技术实现利用位置未知的固定目标对单传感器系统误差的实时精确配准。

1 系统描述与配准算法模型

假设一部二坐标传感器对一固定但位置未知的目标进行探测定位，传感器所在平台能够在公共笛卡尔坐标系中进行一定程度的运动（匀速直线、匀速圆周运动或其他机动运动），设k时刻传感器定位系统获取的自身公共坐标为而相应的传感器真实坐标为(xs(k),ys(k))，则其定位量测方程为

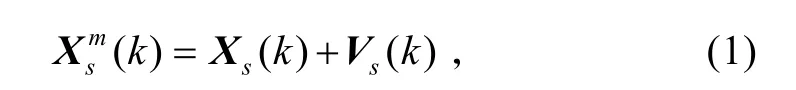
假设传感器具有测距和测方位角系统误差，且分别表示为Δr、Δθ；且传感器具有标准差分别为σr和σθ的零均值高斯分布随机量测误差，分别表示为δr (k)、δθ(k)。

此外，设在公共笛卡尔坐标系中，目标的真实坐标为(x,y)，k时刻目标在传感器局部极坐标系中的真实极坐标为(r (k),θ (k))，则相应的传感器对目标的极坐标测量值为

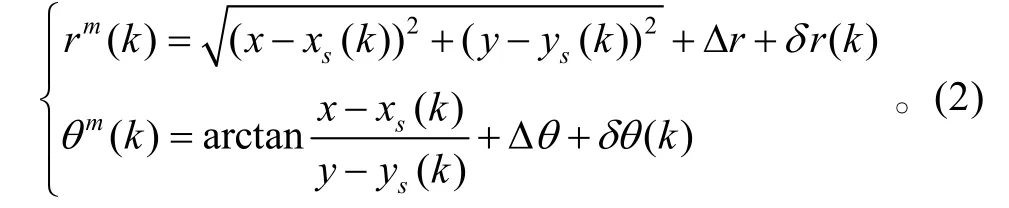
由于上式中传感器位置定位真值需采用测量值代替，而上述测量值只和目标坐标真值与传感器定位量测值间的差值有关。

这样则可将传感器定位随机误差作为目标位置具有一定程度的动态过程噪声来建模。

定义

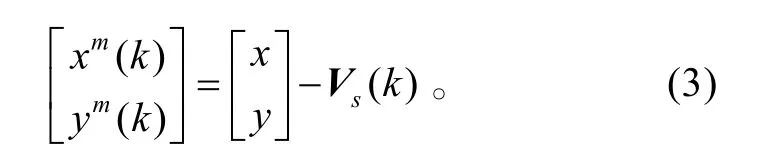
这样，式(2)就相应地转化为

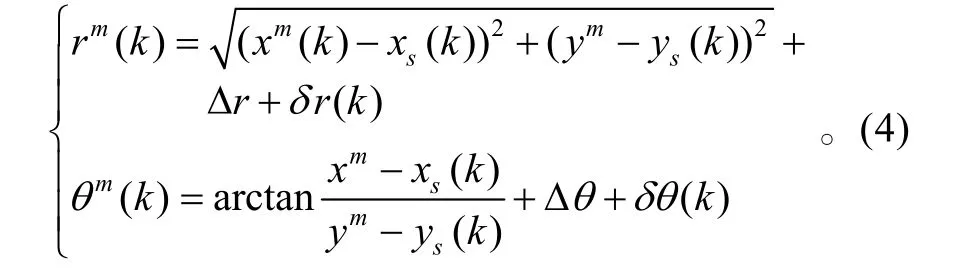
这样，利用k和k−1 两时刻的有关值，定义k时刻的系统状态向量、两时刻量测以及随机误差向量分别为

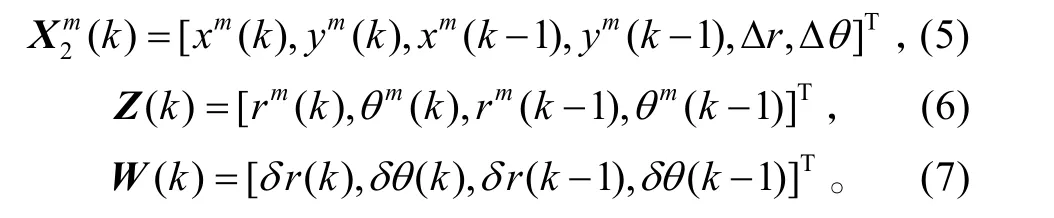
因而，2时刻系统量测方程为

式中：随机量测误差 W(k)的协方差为R(k)。

由式(3)，对于k和k-1 两时刻有

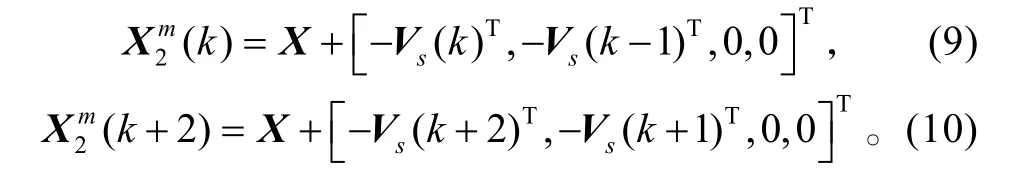
因而，由式(9)、(10)可得系统状态的动态方程为

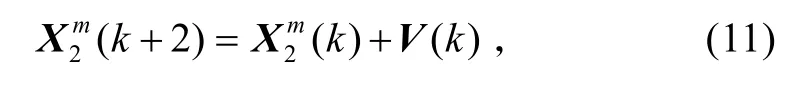
式中，

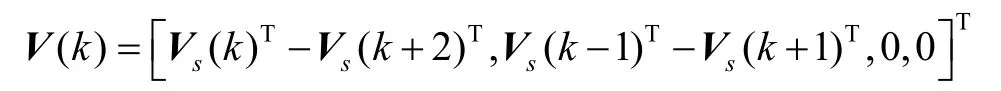
为系统过程噪声，且相应的过程噪声协方差为

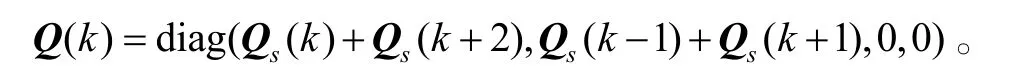
这样，根据式(8)、(11)中给出的系统量测方程和状态方程，可列出相应的两时刻EKF滤波方程组：

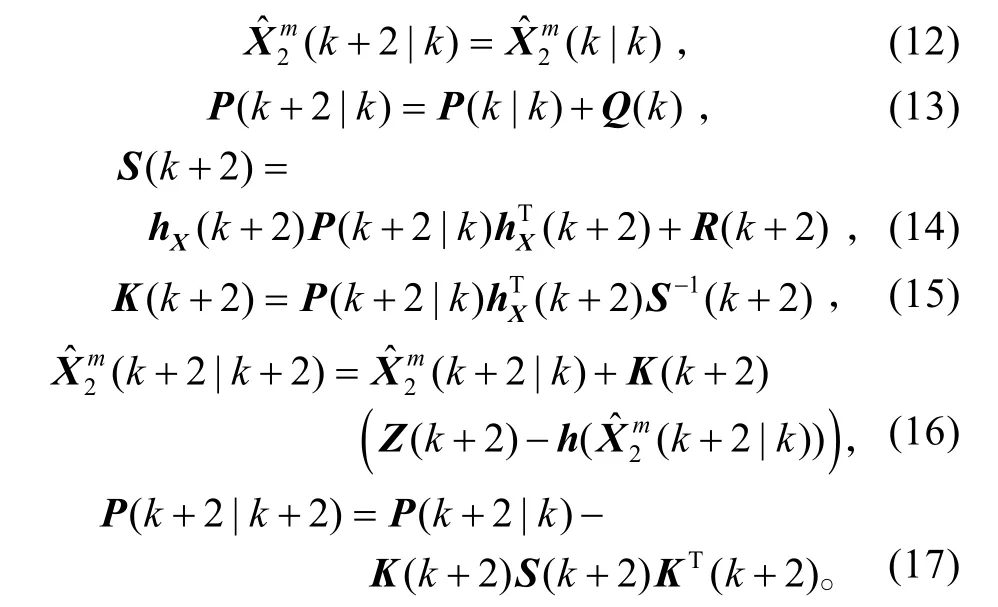
式(14)中，h的雅可比矩阵是

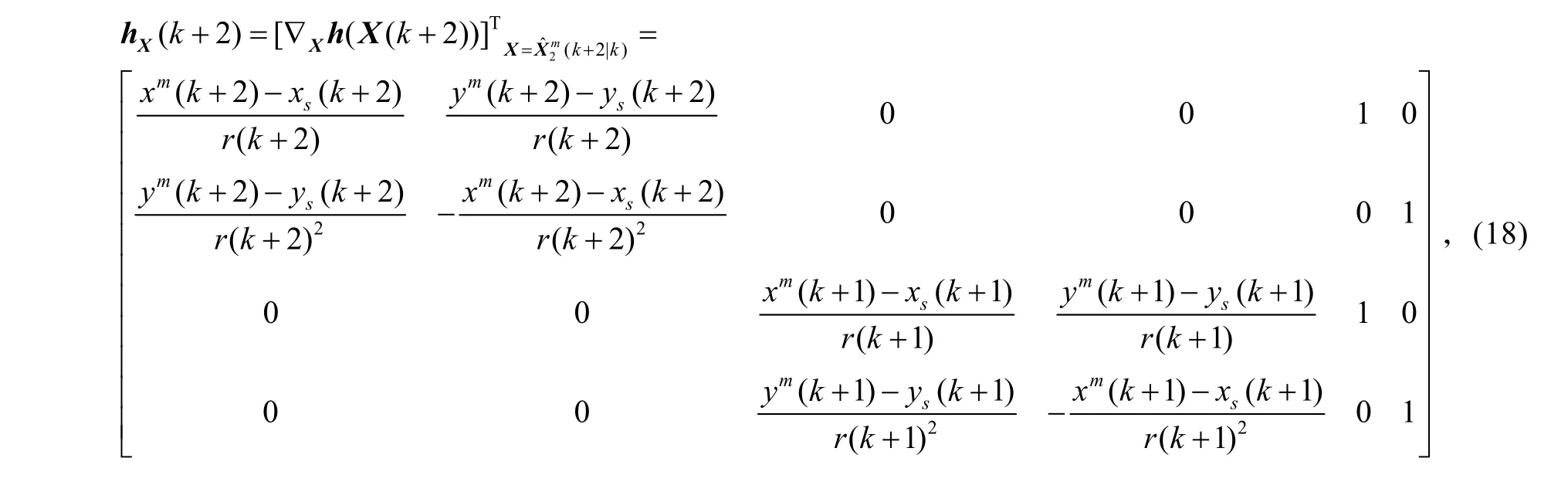
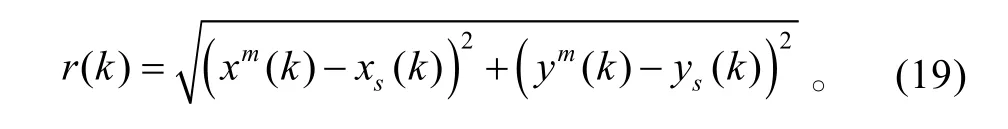
2 仿真验证与分析

采用100次蒙特卡洛仿真，每次仿真时长设置为800 s，采用本文提出的算法模型对单传感器系统误差进行实时估计。

假设传感器探测区域中固定目标的真实位置设为（50 km,50 km）；传感器的测距与测角系统误差分别设置为1 km和1°；传感器自身的定位随机误差标准差为10 m，测距与测角随机误差标准差分别为K×10 m和K×0.1°，其中，K=5,…,10，设上述测量均服从零均值高斯分布。

这里假设传感器做角速度为−0.005 rad/s的匀速圆周运动，且其初始状态为[60 km,0 m/s,50 km,250 m/s]。

仿真结果如图1、图2和表1所示，其中图1、图2分别举例给出了量测随机误差设置K=5时，传感器测距、测角系统误差的单次仿真实时估计曲线；而表1分别列出了在随机误差参数K的几种设置情况下，100次蒙特卡洛仿真后获得的测距和测角系统误差最终估计均方根误差。

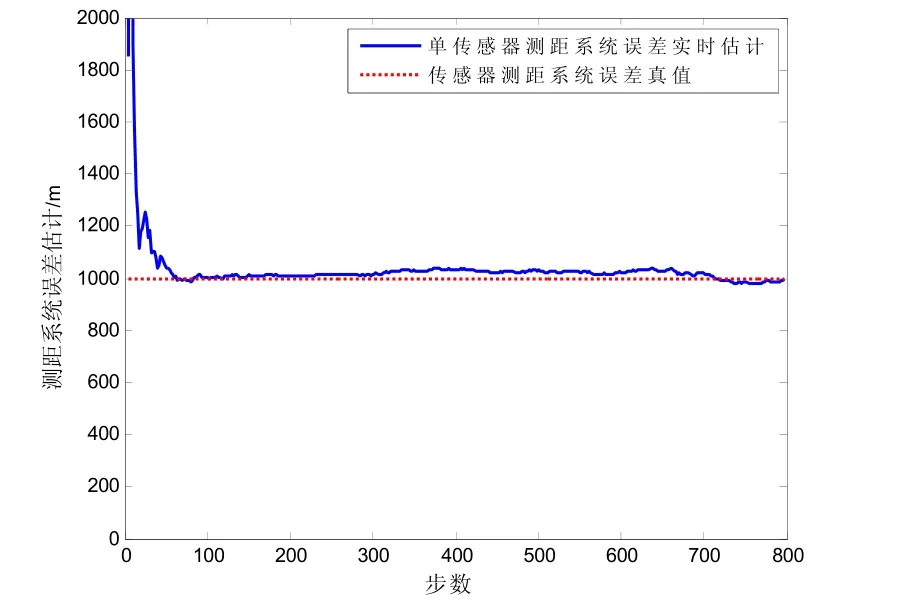
图1 测距系统误差实时估计

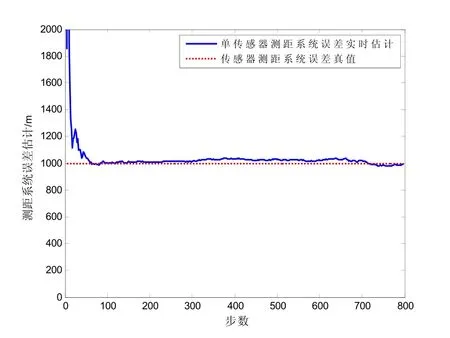
图2 测角系统误差实时估计

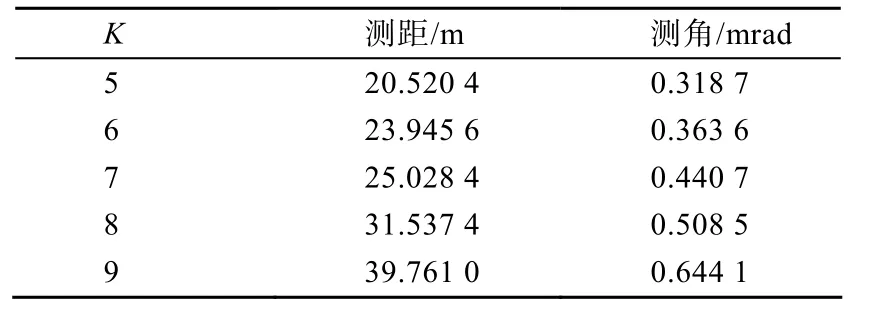
表1 系统误差估计均方根误差

从图1、图2所示的系统误差实时估计曲线可以看出，在K=5的仿真环境中，本文算法对传感器测距、测角系统误差的滤波估计能够迅速地逼近系统误差真值，具有比较快的滤波收敛速度，且对系统误差的估计性能稳定，并显示算法具有较高的实时配准精度。

而由表1中给出的系统误差的最终估计RMSE值可看出，在各种不同参数设置情况下，本文所提出的单传感器实时系统误差配准算法均表现出很好的系统误差配准估计性能，其中对于传感器测距系统误差的估计误差不超过40 m，而对测角系统误差的估计误差最多也不超过0.7 mrad，通过对传感器量测进行误差补偿将能够大幅度地降低系统误差对传感器探测融合性能的影响，这充分说明了本文算法较高的配准性能和算法有效性。

在几种常见传感器测量随机误差（K）的设置情况下，通过对比表1中给出的算法所获得系统误差最终估计均方根误差不难看出，传感器量测随机误差对算法误差配准性能有一定的影响，随着随机测量误差标准差的增大，系统误差估计精度则出现逐渐下降的趋势，但均能较好地满足传感器系统误差配准的需求。

3 结束语

本文对运动平台单传感器系统误差配准问题进行了研究，并提出了单传感器系统误差的实时配准算法。算法无须已知目标位置或目标主动为传感器提供自身导航定位信息，又没有多部传感器间进行协同配准处理的需求，具有滤波结构简单、收敛性好、配准性能稳定等优点。

蒙特卡洛仿真结果验证了本文算法利用固定目标进行单传感器实时系统误差配准的有效性。

[1]董云龙.雷达组网系统中的误差配准技术研究[D].烟台∶海军航空工程学院,2007.

[2]何友,王国宏,关欣.信息融合理论及应用[M].北京∶电子工业出版社,2010∶524-525.

[3]ONG HWA-TUNG.Sensor registration using airlanes∶maximum likelihood solution[C]//Signal and Data Processing of Small Targets.Bellingham,SPIE,2003∶390-399.

[4]PAUL D BUMS,W DALE BLAIR.Sensor bias estimation from measurements of known trajectories[C]//Proceedings of the Thirty-Seventh Southeastern Symposium on System Theory.2005∶373-377.

[5]吴泽民,任姝婕,刘熹.雷达系统误差协同配准算法研究[J].兵工学报,2008,29(10)∶1192-1196.

[6]孙海英.基于协同目标的绝对配准[J].舰船电子工程,2008,28(6)∶94-97.

[7]吴泽民,任姝婕,刘熹.组网雷达系统误差合作校准方法[J].探测与控制学报,2008,30(增刊)∶63-68.

[8]NICKENS OKELLO,BRANKO RISTIC.Maximum likelihood registration for multiple dissimilar sensors[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(3)∶1074-1083.

[9]LIN X D,BAR-SHALOM Y.Multisensor target tracking performance with bias compensation[J].IEEE Trans.on Aerospace and Electronic Systems,2006,42(3)∶1139-1149.

[10]QI YONGQING,JING ZHONGLIANG,HU SHIQIANG.New method for dynamic bias estimation∶gaussian mean shift registration[J].Optical Engineering,2008,47(2)∶1-8

[11]徐毅,陈非,敬忠良,等.基于扩展Kalman滤波的空基多平台多传感器数据配准和目标跟踪算法[J].信息与控制,2001,30(5)∶403-407.

[12]陈非,敬忠良,姚晓东.空基多平台多传感器时间空间数据配准与目标跟踪[J].控制与决策,2001,16(增刊)∶808-811.

[13]何友,宋强,熊伟.基于Fourier变换的航迹对准关联算法[J].航空学报,2010,31(2)∶356-362.