基于连续损伤模型的复合固体推进剂力学性能研究

史 佩，曲 凯，张旭东

（海军航空工程学院 a.训练部；b.飞行器工程系，山东 烟台 264001）

固体火箭发动机中推进剂药柱的结构组成是一种非常复杂的材料结构体系，它主要由模量较低的粘接剂和高体积填充分数的固体颗粒组成。研究表明：推进剂药柱的结构完整性和本构关系直接决定着发动机是否能够正常工作。[1-2]因此，建立合理的损伤和性能劣化模型对于判定固体火箭发动机能否正常工作具有至关重要的意义。

Little和Rice 回顾并总结了如何利用连续损伤理论定量描述推进剂损伤的相关研究工作，并指出如何评价含有一种或多种损伤变量的连续损伤模型好坏的方法。[3]他们总结后发现：目前研究的模型只能成功解释某些特定现象，而不能应用于发动机寿命预估。比如Ozupek[4]提出了考虑损伤的非线性本构方程，该方程只能运用于推进剂单向拉伸试验的模拟。Richard[5]提出利用连续损伤力学模型来研究推进剂力学性能变化，模型中本构关系采用弹性材料本构关系，与推进剂粘弹材料的特性不相符。由此可见，至今还未有一种非常成熟理论来模拟推进剂在多种载荷共同作用下力学性能的变化。

本文在Richard 所提出模型基础上进行改进，无损伤的推进剂应力—应变本构关系利用三元件波因廷模型，来模拟几种常见加载方式情况下推进剂的力学响应。累积损伤采用Bills[6]和Laheru[7]所提出的线性累积损伤模型，连续损伤演化函数采用Stigh[8]所提出的损伤演化函数。

1 线性累积损伤模型

累积损伤模型最先应用于研究金属材料的疲劳损伤，而这其中应用最广泛的是Miner[9]线性累积损伤模型。该模型假定在某一特定载荷下损伤为线性累加，即在特定应力水平 σi下，材料的失效时间为t*，如果假设材料经历了一系列应力水平 σi，每次时间为Δti，如果这时材料破坏，则式(1)成立：

如果Δti无限小，该损伤过程可看作连续过程，上式可转化为积分形式：

式中：t*(σi)为在某一应力 σi作用下材料蠕变破坏时间；tf（蠕变寿命）为在任意载荷作用σ (t)下材料的蠕变破坏时间。

根据Bills[6]和Laheru[7]的试验研究表明：固体复合推进剂同其他材料一样也遵循线性累积损伤破坏规律。

具体形式如下：

式中：σ0代表蠕变应力；t0为在σ0作用下的蠕变寿命；β为通过试验获得材料常数。

Laheru[7]利用上式提出了Lebesgue 正应力N：

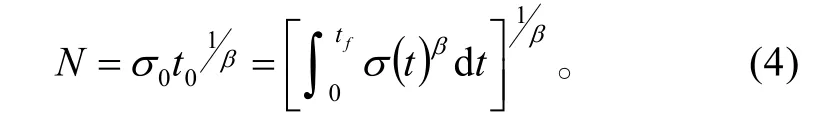
正应力N可解释为在单位时间内使材料失效的蠕变应力，其数值不依赖于材料的载荷史。也就是说，通过试验测量材料的属性N和β后，就可以计算出在任意应力 σ (t)作用下材料的使用寿命。

2 连续损伤模型

连续损伤力学的概念是由Kachanov[10]在1958年发表的论文中提出，该理论在过去的30年里在材料学科的研究过程中发挥着越来越重要的作用，Kachanov在其专著[11]中详细阐述了早期损伤力学的研究工作。

在大多数的连续损伤模型中，损伤被假定为裂纹成核和空穴的生长。而对于推进剂来讲，粘接剂和颗粒之间的脱粘引起的空穴增长是推进剂损伤的重要原因。为了定量描述这些空穴的影响，引入了有效应力和损伤变量D。当D=0时，认为材料无任何损伤，当D=1时认为材料破坏。有效应力可以被看成由于微孔洞和微裂纹的存在而使材料有效承载面积减少后承受的应力，其数学表达式可写成：

一种连续损伤模型必须要考虑损伤的演化，其演化规律可表示成损伤变量D和应力σ的函数：

因此，研究损伤力学其关键就是要确定合理的损伤演化函数。Stigh[8]通过对推进剂蠕变损伤实验研究，给出一种损伤演化方程如式(7)所示：

式中：N为线性累积损伤模型中的Lebesgue 正应力，因此该方程体现了线性累积损伤和蠕变损伤。

3 算例

为了研究推进剂在考虑损伤条件下粘弹响应，推进剂药柱采用三元件波因廷模型来研究，它是由一个弹簧元件和一个马克斯威尔元件构成，见图1。

图1 波因廷粘弹模型示意图

3.1 恒速施加应变

对于恒速施加应变下，有效应力可采用卷积积分法求解：

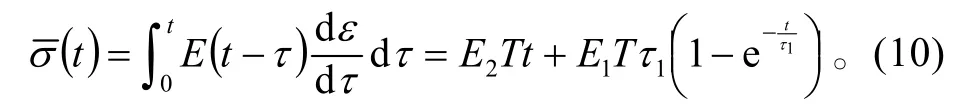
在定应变速率拉伸时推进剂的应力—应变本构关系和损伤演化规律如图2所示。从图中看出：当推进剂应变比较小时，损伤较小，此时推进剂表现为粘弹性；随着损伤逐渐变大，推进剂达到最大应力后迅速破坏。

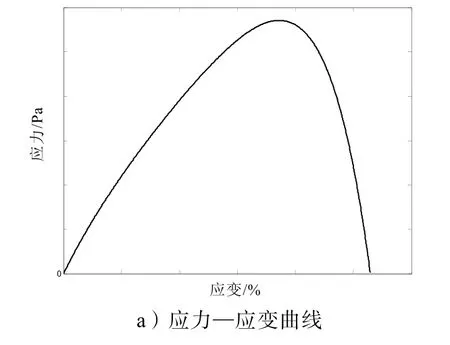
图2 恒速应变拉伸推进剂性能曲线

3.2 蠕变

对于蠕变（σ=σ0），根据文献[12]可知波因廷粘弹模型的蠕变柔量函数为：

将σ代入式(7)并进行积分可求出 D (t)，再利用式(5)、(12)可求解出 ε (t)：

推进剂在蠕变过程中的应变—时间曲线和损伤—时间曲线如图3所示。

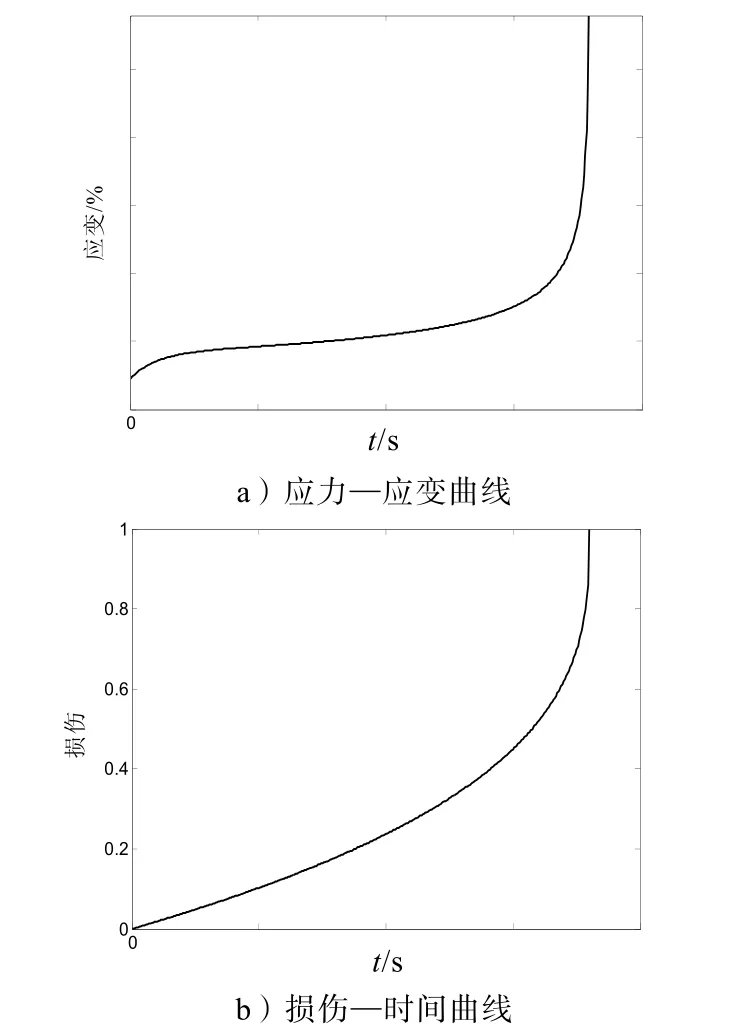
图3 蠕变下推进剂性能曲线

从图3中可看出：推进剂在蠕变过程中应变和损伤都是先缓慢增加，随后迅速变大使其最终破坏。这种趋势与推进剂蠕变试验曲线较为吻合。

3.3 应力松弛

对于应力松弛，取ε=ε0。利用波因廷粘弹模型的松弛模量公式(7)可求解出有效应力

将式(14)代入式(7)中，公式两边积分可求出D (t)，根据式(5)和式(14)可求出 σ (t)：

D (t)没有解析函数表达式，可利用定积分数值求解方法进行求解。推进剂在应力松弛过程中的应力—时间曲线和损伤—时间曲线如图4所示。从图中可看出：初始阶段虽然应力松弛较快，但损伤增加也较快。在曲线后段随着应力松弛逐渐变慢，损伤演化速率也减慢。计算的应力松弛曲线与推进剂试验所测得曲线较为符合，都是开始应力松弛快而后变慢。

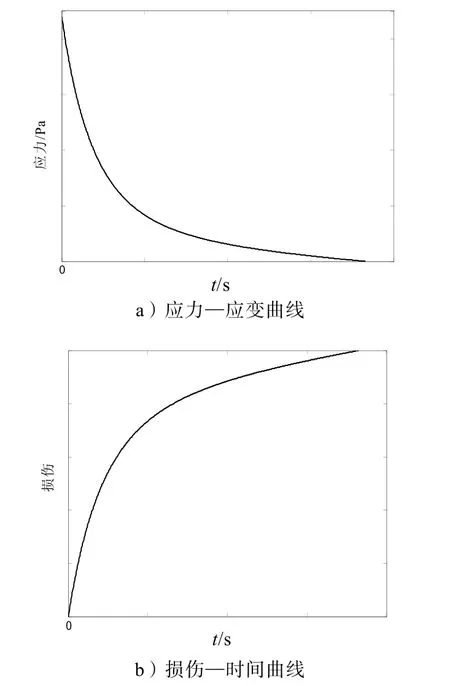
图4 应力松弛下推进剂性能曲线

3.4 定应变幅值往复拉伸

推进剂加载方式为定应变幅值往复拉伸循环试验，其应变幅值和半周期分别为1ε和1t，其曲线如图5a）所示。

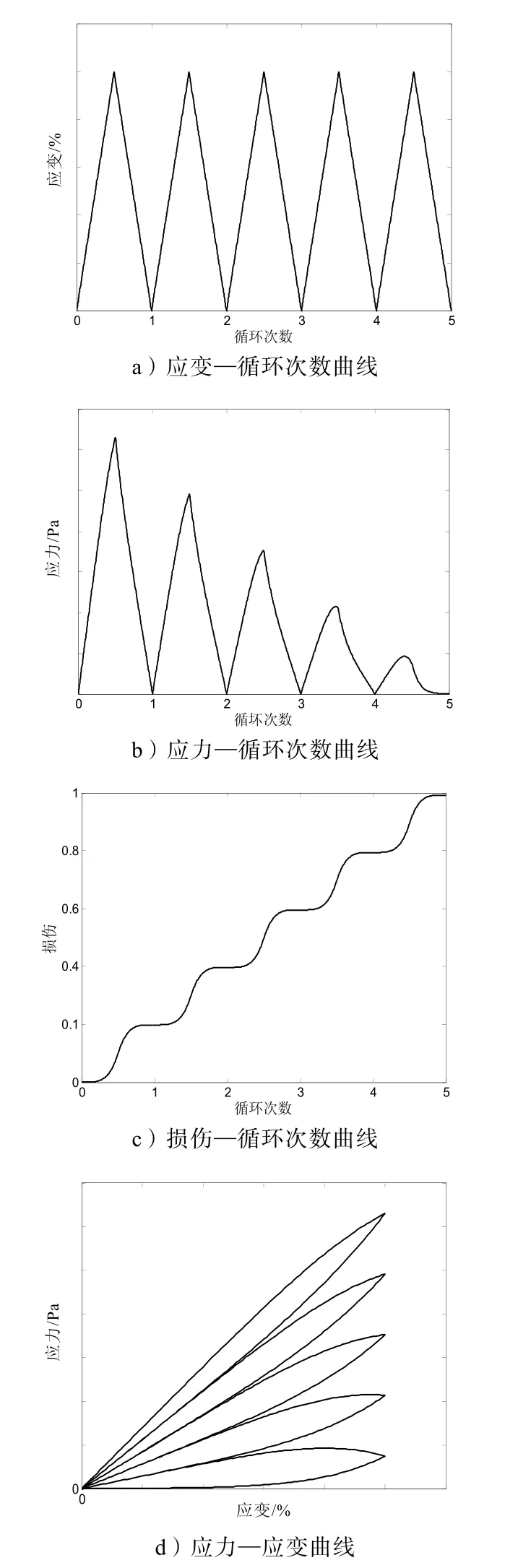
图5 定应变幅值往复拉伸下推进剂性能曲线

根据3.1 恒速施加应变的情况，可知推进剂应力—应变关系如式(10)所示，它可进一步化简：

当在应变循环的2(n−1)

t1≤t≤(2 n−1) t1周期：

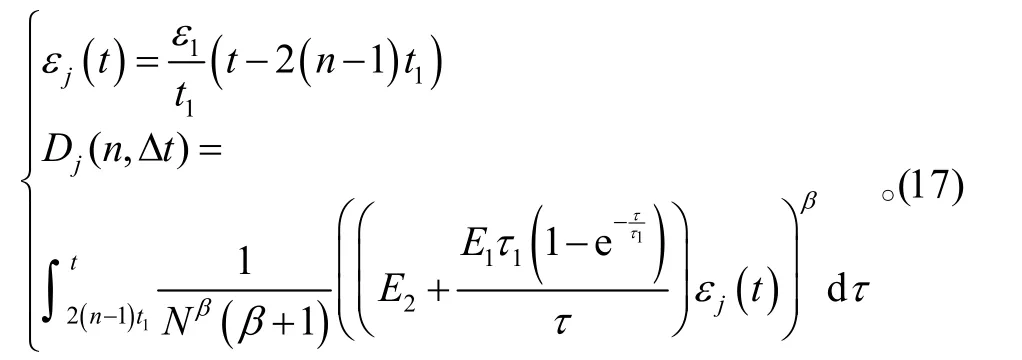
当在应变循环的(2 n−1)t1≤t≤2nt1周期：

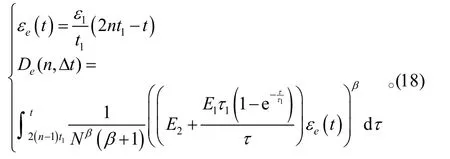
通过式(17)和式(18)可计算出每一周期的损伤量，将其累加起来可以得到总损伤，并可进一步求出应力的变化。

当2(n−1) t1≤t≤(2 n−1) t1时，

当(2 n−1) t1≤t≤2nt1时，

推进剂在定应变幅值往复拉伸循环试验中的应力—循环次数曲线、损伤—循环次数曲线和应力—应变曲线如图5b）～ d）所示。从图中可看出：推进剂损伤值随着循环次数的增加而不断增加；推进剂的最大应力随着循环次数的增加而不断减少，且应力在下降段随着循环次数的增加斜率逐渐变缓。

4 结论

结合累积损伤与连续损伤力学相关理论，建立了复合固体推进剂蠕变累积损伤模型，通过算例可得到以下结论：

1）利用本模型可以模拟推进剂在不同加载方式下应力—应变本构关系。

2）采用波因廷模型来模拟其无损本构关系，比文献[5]提出的弹性模型能更好模拟推进剂的力学响应。

3）计算所得曲线与推进剂试验所得曲线变化趋势较为吻合，可解释试验过程中出现的一些现象，它为理论计算推进剂损伤提供了一条有效可行的途径。

[1]蒙上阳,唐国金,雷勇军.材料性能对固体发动机结构完整性的影响[J].国防科技大学学报,2002,24(5)∶10-15.

[2]邢耀国,董可海.固体火箭发动机寿命预估研究的发展和展望[J].固体火箭技术,2001,24(3)∶1-4.

[3]LITTLE R R,RICE J R.Investigating damage in composite solid propellant[C]//Proceedings of the 34thJANNAF Structures and Mechanical Behavior Subcommittee Meeting.Chemical Propulsion Information Agency Publication,2001,706∶65-80.

[4]OZUPEK S.Constitutive modeling of high-elongation solid propellants[J].Journal of Engineering Materials and Technology,1992,114∶111-115.

[5]RICHARD K K.Continuum damage mechanics modeling of solid propellant[C]//44thAIAA/ASME/SAE/ASEE Joint Propulsion Conference.Hartford,CT,2008.

[6]BILLS K W.Observations on the linear cumulative damage concept[C]//Proceedings of the JANNAF Structures and Mechanical Behavior Subcommittee Meeting.Chemical Propulsion Information Agency Publication,1980∶57-59.

[7]LAHERU K L.Development of a generalized failure criterion for viscoelastic materials[J].Journal of Propulsion and Power,1992,8∶756-759.

[8]STIGH U.Continuum damage mechanics and the life-fraction rule[J].Journal of Applied Mechanics,2006,73∶702-704.

[9]MINER M A.Cumulative damage in fatigue[J].Journal of Applied Mechanics,1945,12∶159-164.

[10]KACHANOV L M.On the Creep Fracture Time[M].Izv.Akad.Nauk USSR,1958∶26-31.

[11]KACHANOV L M.Introduction to Continuum Damage Mechanics[M].Martinus Nijhoff Publishers,1986.

[12]牛秉彝.高聚物粘弹及断裂性能[M].北京∶国防工业出版社,1992∶16-20.