舰载机维修保障力量需求研究
韩 维,商兴华,李 成,刘 明
(1.海军航空工程学院 a.七系;b.研究生管理大队,山东 烟台 264001;2.海军驻景德镇昌河飞机工业公司军事代表室,江西 景德镇 333000)
0 引言
舰载机所处的环境比陆基飞机恶劣,其结构也比陆基飞机复杂,发生故障的概率更高,加之现代战争对舰载机出动强度大、时间紧的要求,必须部署足够的维修保障力量维持其战备完好率,这样才能最大限度地利用舰载机,使有限的飞机发挥最大的作战效能。但是对于载舰这样一个空间有限的“海上机场”而言,只能搭载数量有限的维修保障力量,过多的维修保障力量会造成有限资源的浪费,必须根据舰载机作战任务和维修保障要求进行部署。
维修,是为使装备保持、恢复到或改善其规定技术状态所进行的全部活动[1]。舰载机舰上维修保障力量包括舰基基层级的维护机组以及舰基中继级的维修组(由于本文研究的是维修保障活动,以下将二者统称为维修组),维修组的数量以及维修效率直接影响舰载机的战备完好率。战备完好率是装备战备完好性的度量,指的是当要求装备系统投入作战时该系统能够遂行任务的概率[2]。为简化计算,本文定义舰载机的战备完好率为一段时间内可用于执行任务的完好舰载机数量与舰上所有舰载机数量之比,这样定义的战备完好率比实际的战备完好率稍小,所以为达到某一战备完好率水平,对维修保障能力的要求更高,有利于实际战备完好率水平的实现。
维修保障过程是典型的排队过程,应用排队论研究飞机维修保障的文章较多[3-4],但是以此构建的模型并不能清楚地反映各状态飞机数量的动态变化情况。文献[5]应用动态平均值法建立了维修保障系统效能评价模型,讨论了维修系统主要参数对保障效果的影响。本文以此模型为基础研究舰载机的维修保障,考虑了故障飞机不可修复以及舰基基层级由于维修能力不足导致飞机转入舰基中继级进行维修的实际情况,使得原模型更加完善。
1 假设与前提
1)假定舰面保障m架舰载机,舰载机维修保障力量包括舰基基层级和舰基中继级两个级别,部署舰基基层级维护机组数量为1C,中继级维修组数量为C2,不考虑舰载机送交基地维修的情况。这样,舰载机处于 4种状态:完好、在舰基基层级进行或等待维修、在舰基中继级进行或等待维修、超出维修能力不能维修,数量分别为1m、2m、3m和4m。
2)舰载机返回载舰维修服从参数为λ的泊松流[6],即单位时间(d)平均有λ架次飞机发生故障返回载舰进行维修,其中一部分进入舰基基层级进行维修,比例为1p,一部分进入舰基中继级进行维修,比例为p2,还有一部分由于超出舰上维修能力而进行封存,这部分列为损失的飞机,比例为p3,且p1+p2+p3=1。
3)进入舰基基层级维修的舰载机,还会有一部分由于故障情况超出基层级维修能力转入中继级进行维修,呈强度为λ2的泊松流。
4)舰载机在舰基基层级和中继级修复时间分别服从参数为μ1和μ2的负指数分布[7]。
由上述条件可得舰载机状态转移过程见图1。
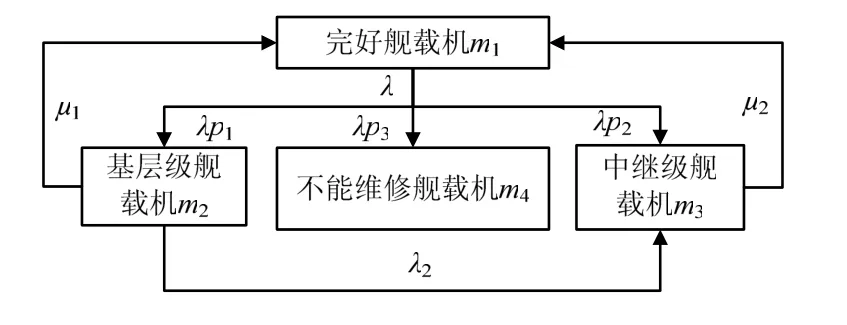
图1 舰载机状态转移图
5)每个级别的维修组在一定时间内只负责一架飞机的维修工作,即不会出现两个或者多个维修组共同维修一架飞机的情况。
6)每个级别的维修组只负责本级别的维修工作,即中继级维修组不会加入基层级工作,基层级维修组也不会加入中继级工作。
7)当需要维修的舰载机数量多于维修组数量时,一部分舰载机等待维修;当需要维修的舰载机数量少于维修组数量时,一部分维修组处于空闲状态。
2 飞机状态转移模型构建
由前述条件可知,当需要维修的舰载机数量多于维修组数量时,所有的维修组都要进行维修工作;当需要维修的舰载机数量少于维修组时,只有与待维修的舰载机数量相等的维修组进行维修工作,其余的维修组处于空闲状态。所以构建舰载机状态转移模型时,应根据维修组与待维修的舰载机数量关系,分情况进行研究。
当m2≤C1、m3≤C2时,由图1可以确定 Δt时间内Δm1、Δm2、Δm3和Δm4的变化量为

两边同除以 Δt,并令Δt→0,加上附加方程,可得方程组

当m2≤C1、m3>C2时,在中继级有 C2个维修组进行维修保障,将上式 μ2前 m3换成 C2即可,此时方程组如式(3)。
同理,可得到m2>C1、m3≤C2和m2>C1,m3>C2时的状态转移方程,如式(4)、(5)。
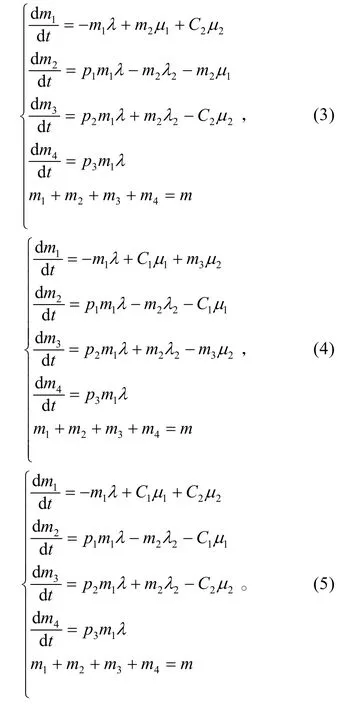
设m=24,C1=16,C2=3,μ1=1/6,μ2=1/16,λ=1/10,λ2=1/100,p1=0.82,p2=0.15,p3=0.03。
当t=0时,m1=24,m2=0,m3=0,m4=0,通过上面方程组仿真[8]出50 d过程中平均各状态舰载机数量随时间变化曲线如图2所示。

图250 天过程中平均各状态舰载机数量随时间变化曲线
由图2可以看到,随着飞行时间的不断增加,完好舰载机平均数量越来越少,但是减少的趋势不断变小并逐渐趋于相对稳定;处于舰基基层级的舰载机平均数量开始急剧增加,但是时间超过15 d后,开始有逐渐减少的趋势;处于舰基中继级维修及损毁的舰载机平均数量不断增加。
3 不同维修保障能力下完好舰载机数量变化
3.1 维修组数量对完好舰载机数量变化情况的影响
当C1=16,C2=1、2、3、4的情况下,平均完好舰载机数量随时间变化曲线如图3所示。

图3 不同舰基中继级维修组数量下平均完好舰载机数量随时间变化曲线
由图3可知,在假设条件下,前5 d飞行过程中舰基中继级维修组数量变化对平均完好舰载机数量几乎没有任何影响,而过了5 d之后,影响逐渐表现出来。到了50 d时,安排 4个中继级维修组要比安排1个维修组完好飞机数增加 4到5架左右;当中继级的维修组数量多于 4个时,变化曲线基本上与安排 4个中继级维修组时重合,说明此时安排4个中继级维修组时保障效率已达最高,再安排更多的维修组会带来人力、物力资源的浪费。
当C2=4,C1=15、16、17的情况下,平均完好舰载机数量随时间变化曲线如图4所示。

图4 不同舰基基层级维修组数量下平均完好舰载机数量随时间变化曲线
由图4可知,当中继级安排了4个维修组时,在基层级安排15个、16个或更多维护机组,平均完好舰载机数量变化曲线基本重合,说明维修保障效果基本相同。这说明并不是维护机组越多保障效果越好,应综合考虑机务保障和维修保障的要求来设置。
3.2 维修保障效率对完好舰载机数量变化情况的影响
在C1=16、C2=4、μ2=1/16的情况下,μ1=1/2、1/6、1/8时平均完好舰载机数量随时间变化曲线如图5所示。

图5 不同舰基基层级维修组维修效率下平均完好舰载机数量随时间变化曲线
由图5可知,在此条件下,基层级的维修效率对平均完好舰载机数量影响较大,当基层级的维修效率分别为1/2、1/6和1/8时,平均完好舰载机数量逐渐减小;随着时间增加,不同维修保障效率带来的差异有逐渐减小的趋势;此条件下,50 d时可以分别保证16、13、11架舰载机处于完好状态,此时战备完好率分别为66.67%、54.17%、45.83%。
在C1=16、C2=4、μ1=1/2的情况下,μ2=1/10、1/16、1/20时平均完好舰载机数量随时间变化曲线如图6所示。

图6 不同中继级维修组维修效率下平均完好舰载机数量随时间变化曲线
图6形状与图5有较大的差异,说明中继级维修组维修效率与基层级维修组维修效率对平均完好舰载机数量影响的情况有所不同,随着时间增加,不同维修保障效率带来的差异逐渐变大。在50 d左右处,中继级的维修效率由1/20增大到1/10,平均完好舰载机数量增加1架左右。
4 舰载机维修保障能力需求分析
分析舰载机维修保障能力,关键是根据舰载机的战备完好率要求进行维修保障力量的部署。
假如要求舰载机战备完好率不低于80%,由前述分析可知,在舰载机故障率 λ=1/10的情况下,通过改变各级维修组的数量和维修效率,仍不能满足战备完好率要求,说明这时舰载机的可靠性是制约其达到此战备完好率的关键因素。要想使舰载机达到80%的战备完好率,应增大舰载机的可靠性,然后通过改变那些反映维修保障能力的参数,找出满足预定战备完好率且较优的参数组合,这样就得到了满足一定战备完好率的维修保障需求。
假如舰载机的可靠性提高,其故障率为λ=1/20,当C1=16、C2=4、μ1=1/2,μ2为1/20、1/16、1/10时舰载机战备完好率随时间变化曲线如图7所示。

图7 不同中继级维修组维修效率下舰载机战备完好率随时间变化曲线
由图7可知,随着中继级维修组维修效率的提高,舰载机战备完好率逐渐增大,当中继级维修组维修效率 μ2=1/10时,在第50 d时舰载机的战备完好率为80.44%,说明这时可以保证舰载机在50 d过程中保持至少80%的完好率水平。通过改变基层级维修组的维修效率可以达到同样的效果。
当μ1=1/2、μ2=1/10、C1=16、C2=2,3,4时舰载机战备完好率随时间变化曲线如图8所示。

图8 不同中继级维修组数量下舰载机战备完好率随时间变化曲线
如果C2不变,C1变化,其效果与图8相同。
假如舰载机的可靠性提高,其故障率为λ=1/30,当C1=16、C2=4、μ1=1/2、μ2=1/10时舰载机战备完好率随时间变化曲线如图9所示。
由图7、图8可知,在上述条件下决定舰载机战备完好率的因素是维修组的维修效率,而与维修组的数量无关。由图7~9可知,舰载机的故障率对其战备完好率影响较大。所以,要想使得舰载机保持在80%的战备完好水平有两个途径:一是加强维修保障人员的培训,保证有足够的维修保障资源,以此提高维修组的维修保障效率;二是提高舰载机的可靠性水平,降低其故障发生概率。
由算例结果可知,由于舰基基层级的维修组实际就是维护机组,其数量较大,处于舰基基层级待维修和正在维修的飞机数量之和小于基层级维修组的数量,即 m2>C1的情况并没有发生,方程(3)、(4)并没有起作用,这是将实际算例应用于该模型,由于实际情况的特殊性所致。
5 结论
维修保障力量是影响舰载机战备完好率的关键。本文通过构建维修保障力量与平均完好舰载机数量关系的数学模型,分别讨论了各种反映维修保障力量的参数对舰载机战备完好率的影响。可见,在本文给定条件下,舰基基层级维修组的保障能力与中继级维修组的保障能力对维修保障效果的影响有所不同;维修组的数量并不是越多越好,应根据实际情况进行部署。在本文条件下,可以通过提高维修组的维修效率和舰载机自身的可靠性这两个途径使得舰载机达到80%的战备完好率。
[1]甘茂治,康建设.军用装备维修工程学[M].北京∶国防工业出版社,1999∶97-102.
[2]《可靠性维修性保障性术语集》编写组.可靠性维修性保障性术语集[M].北京∶国防工业出版社,2002∶28-29.
[3]吴勇,董惠茹,王俊攀.M/M/C/m/m 排队系统模型的飞机战伤抢修研究[J].电光与控制,2009,16(4)∶90-92.
[4]岳奎志,韩维,王庆官.基于排队论的机群出动能力模型[J].海军航空工程学院学报,2009,24(2)∶224-228.
[5]唐铁军,徐浩军,华玉光.动态平均值法评估航空装备一线维修保障效能[J].电光与控制,2007,14(4)∶191-194.
[6]郝杰忠,杨建军,杨若鹏.装备技术保障运筹分析[M].北京∶国防工业出版社,2006∶32-40.
[7]唐应辉,唐小我.排队论—基础与分析技术[M].北京∶科学出版社,2006∶14.
[8]张德丰.Matlab数值分析与应用[M].北京∶国防工业出版社,2007∶211-232.

