基于单天线的模式滤波测角方法
朱晓丹,裴泽霖,王克让,陈 卓,朱伟强
(1.中国航天科工集团8511研究所,江苏 南京 210007; 2.北京遥感信息研究所,北京 100192)
0 引言
角度估计是雷达、侦察、导航等领域的重要内容,按照观测量的不同,角度估计方法大致可以分为比幅测角、比相测角、时差测角等[1]。其中,比相测角和时差测角方法需要形成基线,时差测角需要2个接收天线和通道,基线相对较长;比相测角主要包括相位干涉仪、空间谱估计测角,一般要求多个接收天线和通道。比幅测角方法通过比较多个天线/波束信号幅度的相对大小得到目标角度估计,最少只需要一个天线。由于原理简单,且信号幅度易于测量,比幅测角方法得到较早的研究和发展。常见的比幅测角方法包括最大幅度搜索法[1]、最小幅度搜索法[2-3]、多天线/波束比幅法[4]以及和差波束法[5]等。但是,传统比幅测角方法一般要求天线或波束的主瓣对准目标方向,因而只利用到了方向图的主瓣信息,进一步提高测角精度需要充分利用天线在不同方向上获取的信息。文献[6~8]研究了利用旋转单天线实现测角的方法,提出了最大似然估计方法,但需要进行搜索求解,算法计算量大。文献[9]基于最大后验概率函数提出一种迭代解卷积方法,可实现超分辨率测角。文献[10~11]将旋转单天线测角问题转化为谱估计模型,并基于有限更新率采样理论,提出一种超分辨率估计方法,但需要通过零化滤波等方法求解,计算复杂度较高。文献[12]基于正交匹配追踪方法估计出目标角度。文献[13~14]将天线看成是传输函数,接收信号功率则是天线方向图与观测角度的卷积,因而提出一种基于傅里叶变换和解卷积的求法。尽管上述方法给出了目标角度的估计,但普遍存在计算复杂较高的问题,且通常将天线主瓣近似为高斯函数,引入了模型误差,因此也难以实现高精度测角。为了避免传统比幅方法的不足,并实现低复杂度测角,受文献[15~16]中幅度加权测角方法的启发,本文提出一种基于模式滤波测角方法,首先将天线方向图表示为指数和形式,再通过加权实现对特定天线模式的选择,将问题转化为可解析估计的模型,同时推导得到理论精度和无模糊测角范围。1 传统比幅测角方法单天线在旋转圆周上两个不同的观测点处接收角度为θ0的目标信号,2次观测间隔角度为Δθ。由于接收角度的不同,接收到的目标信号存在功率的差异,比较2次接收信号功率的相对大小即可实现对角度的估计,假定天线方向图为F(θ),两次接收到的信号的功率分别为p1、p2,则有:p2/p1=Fθ0-Δθ/Fθ0
(1)
因此,可由天线方向图建立比幅测角查找表,根据p2/p1确定目标角度。也可以将天线主瓣拟合为二次函数推导解析解,如将天线主瓣拟合为式(2)所示的形式:
F(θ)=aθ2+c
(2)
式中,a、c为二次拟合系数;θ∈[-θm,θm],θm为拟合的主瓣宽度,如取3dB波束宽度,其大小影响拟合的精度以及最大交叉角度Δθ,一般有Δθ<θm。则有:
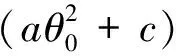
(3)
此时可根据p2/p1结合拟合系数求得:
Δθ+(a2Δθ2p1p2-ac(p1-p2)2)1/2)/a(p1-p2)
(4)
这种比幅测角方法原理简单,容易实现,但一般需要在主瓣内接收信号,测角精度和测角范围与方向图主瓣形状有关,通常主瓣越窄、主瓣内增益变化越大,测角精度越高,但测角范围也越小,在实际应用中一般难以实现高精度测角。
2 旋转单天线测角模型
为了提高测角精度,需要充分利用天线在不同方向上接收到的角度信息[17]。如图 1所示,接收天线围绕圆点O旋转并以不同角度接收来自TO方向的目标信号,图1中箭头表示天线旋转方向,粗实线表示天线方向图。假定在旋转圆周上共有Q个均匀分布的观测角度,称为观测点。天线方向图增益表示为F(θ),对角度为θ0的目标信号,假设利用增益为0dB的天线接收到信号的平均功率为P0(P0>0),则各观测点θq收到的信号平均功率rq(q为观测点序号,0≤q≤Q-1)为:rq=P0F(θ0-θq)
(5)

图1 旋转单天线测角示意图
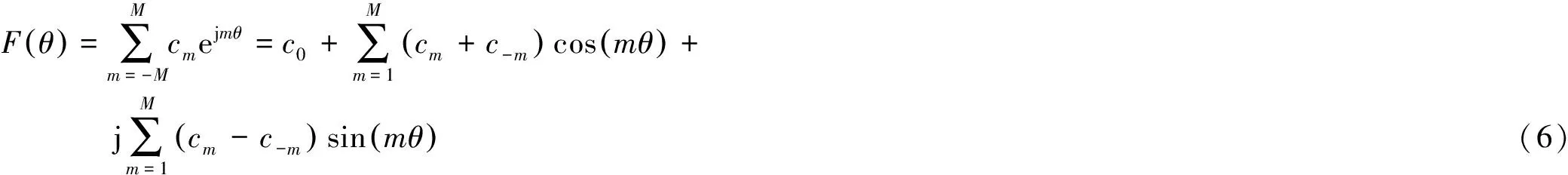
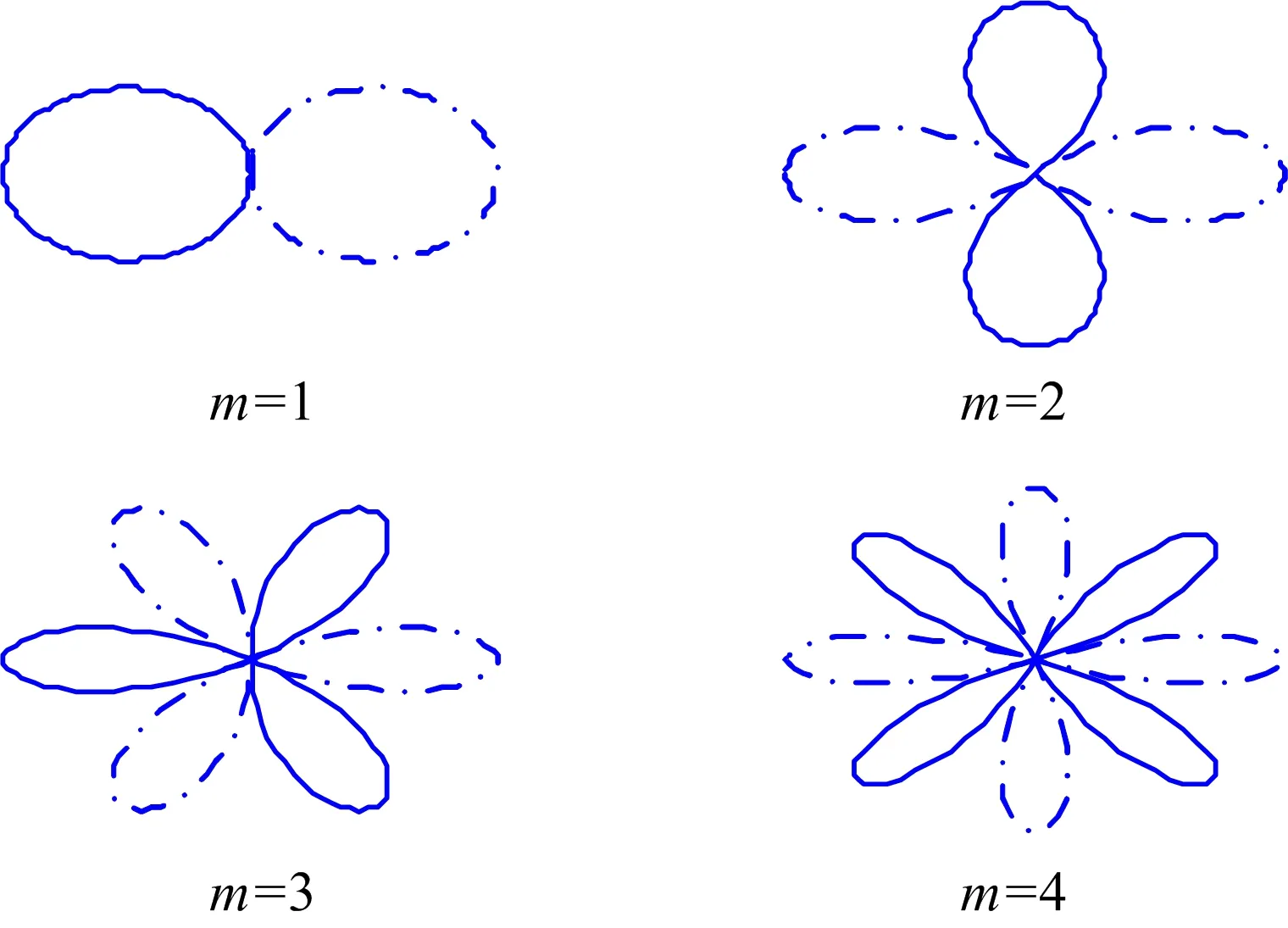
图2 不同模式下的天线方向图分量
3 基于模式滤波的角度估计
3.1 模式滤波算法

(9)
此时,如果m=pN+l只有一组解,或仅有一组解对应的cm不为零,将该解记为cm0,则有:
gl=P0Ncm0ejm0(θ0-θd)
(10)
(11)
式中,φ为cm0的相角,称为模式相位,即tanφ=lm(cm0)/Re(cm0)。从上述求解方法可以看出,加权求和实现了对模式的滤波,从而将角度估计模型转化为解析形式。
3.2 加权参数l和模式m的选择
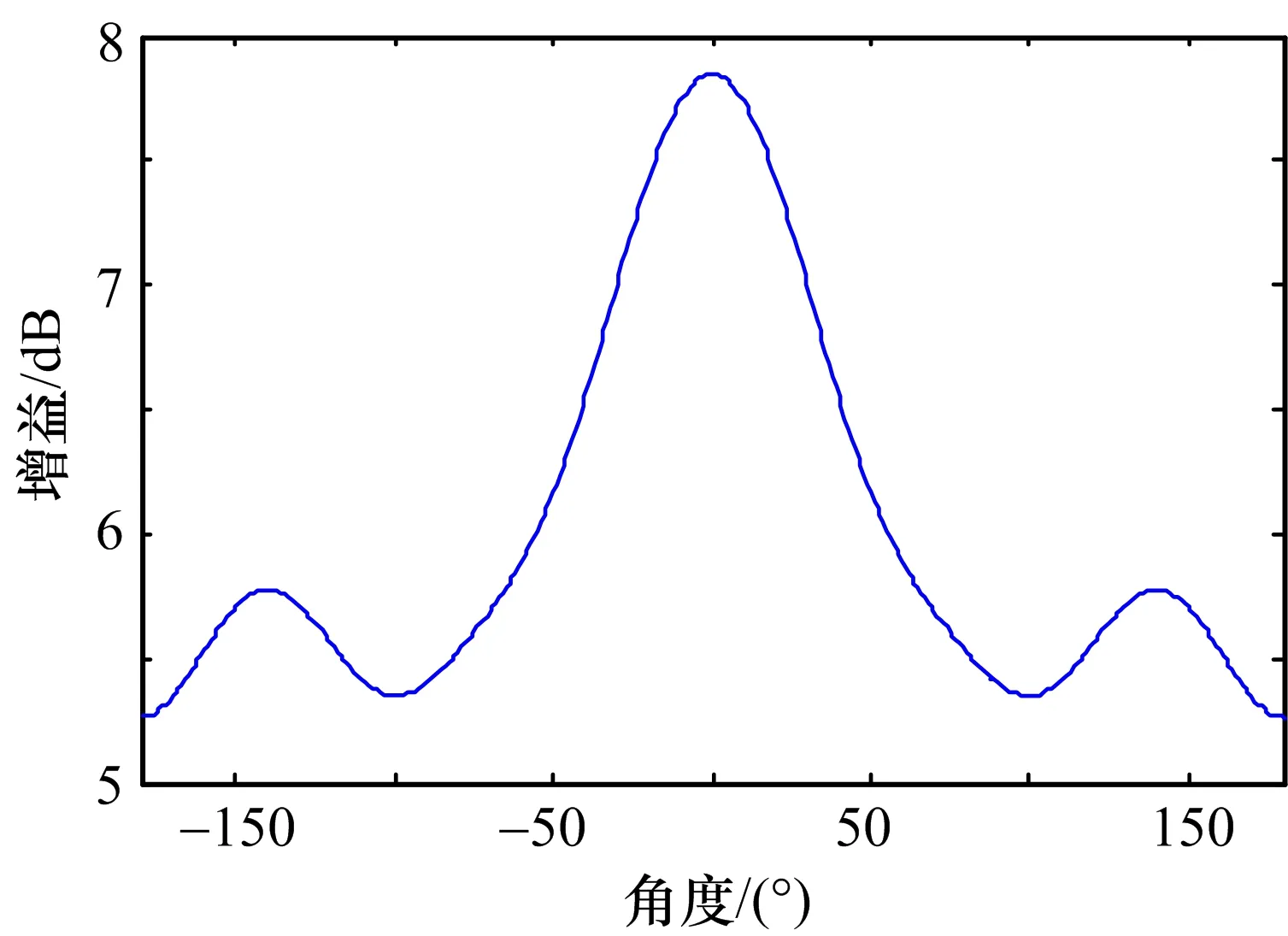
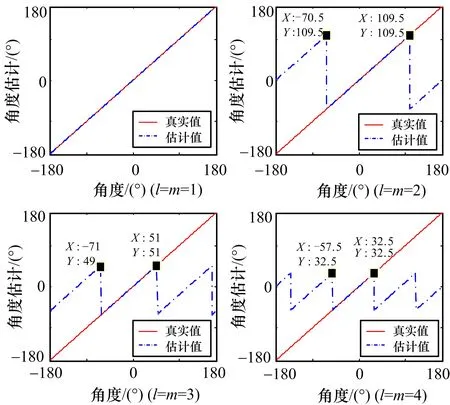
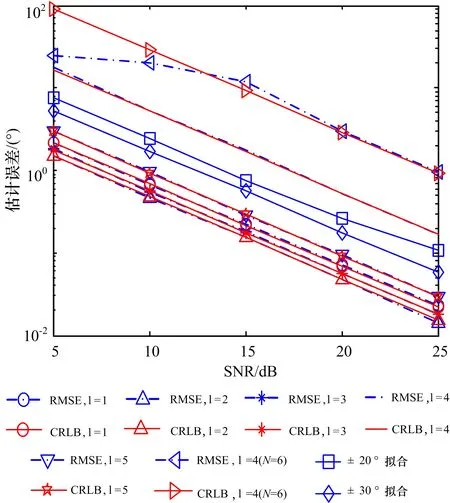
上一节指出,式(10)成立的条件是m=pN+l只有一组解,或仅有一组解对应的cm不为零。由-M≤m≤M可以得到-(M+l)/N≤p≤(M-l)/N,则p的取值范围最多为2M/N(表示不小于 2M/N的最小整数)。1)当N>2M时有-2-1-(l/N) 表 1 M=5时加权参数和模式的选择(c-5=c5≠0) 从本节的分析可以看出,可通过选定l和加权运算实现对cm的选择。对于旋转单天线,N>2M是容易满足的,只需要在旋转方向选择足够的观测点;而如果N较小,为了使用模式滤波测角方法,需要天线满足一定的条件,即特定的模式为零或非零。 为了估计角度,还需要知道φ,φ为实际天线的参数,可通过天线的测试计算得到。在K个不同的方向接收同一测试信号,信号功率记为r(θk)(k=1,…,K)。假定天线方向图关于0°对称,根据式(7)整理成向量形式为: (12) (13) 根据式(11)可以知道,由于arctan(·)函数可以得到[-π,π]的解值范围(结合g的实部、虚部的正负性),因此无模糊测角范围为[-(π+φ)/m0,(π-φ)/m0],超过这一范围将出现测角模糊,模糊周期为2π/m0。实际上,经过模式滤波,天线方向图的有效分量为2Re(cm)cos(mθ),为关于θ的周期函数,因而采用模式滤波法进行测角时,本质上是采用图 2中所示的各种周期性的方向图天线进行测角,因而出现了模糊问题,结合cos(mθ)的正负性可知,无模糊范围的大小分别为2π、2π/2、2π/3、2π/4。由图 2可以知道,m0越小,无模糊测角范围越大;在没有其它先验信息的条件下,为了在[-π,π]范围内无模糊测角,需要保留m0=1的模式。 根据式(10)可得:Re(gl)=P0N|cm0|cosφ′ (14)lm(gl)=P0N|cm0|sinφ′ (15) 式中,φ′=m0(θ0-θd)+φ。由于P0未知,对式(14)、式(15)进行微分,可整理为: (16) (17) (18)上述证明中用到了Re(a)Re (b)=2-1Re(abH+ab),H 表示对向量a或b的共轭转置。类似地,根据Im(a)Im(b)=2-1Re (abH-ab),Re(a)Im(b)=2-1Im (abH-ab),可求得: Ι2 (19) 式中,Ι2为二阶单位矩阵。代入式(17)可求得: (20) 如果对估计式(11)进行误差推导,得到的测角精度与式(20)相同,因此式(11)所示的算法可以达到理论精度,这里不再详细描述推导过程。由式(20)可以看出:1)测角误差与m0成反比,根据前一节的分析可以知道,无模糊测角范围也与m0成反比,即出现了无模糊测角范围和测角精度的矛盾;测角精度与|cm0|成反比,对特定的天线,可通过式(20)计算出不同模式对应的理论估计精度,从而选择特定的模式进行测角。2)在同样的模式下,观测点数越多,测角精度越高;信噪比越高,测角精度越高。3)估计精度与起始观测角度θd和待估计角度θ无关,因此,天线主瓣是否对准目标对测角性能没有影响。为了提高测角精度并兼顾无模糊测角范围,可以选择较小的模式保证较大的无模糊测角范围,同时提高cm0,并选择足够多的观测点数保证较高的测角精度。 图3 随机产生的天线方向图 图4 无模糊测角范围 图5 测角精度与模式和SNR的关系 下面对本文提出的旋转单天线模式滤波测角进行仿真分析。将天线量化为共计M=5个模式,随机产生的c0~c5为4.067、0.437、0.314、0.180、0.014、0.065,图 3给出了天线方向图。下面结合该天线进行仿真分析。仿真中,利用增益为0 dB的天线接收到信号的平均功率P0为1。仿真1(无模糊测角范围分析):选择N为180,此时令l=m即可实现对cm的选择。图 4给出了不同模式下的无模糊测角范围,可以看出,m越大,无模糊测角范围越小,与理论分析得到的2π/m一致。仿真2(模式和信噪比条件对测角性能的影响分析):仿真中目标角度为5°,信噪比(P0/σr)范围为5~20dB,在旋转圆周上均匀选择180个观测点,进行1000次Monte-Carlo仿真,统计测角误差。图 5给出了不同信噪比条件下,测角误差与模式的关系。为了与传统比幅测角方法进行对比,图 5还给出了同样信噪比条件下利用该天线进行比幅测角的精度,利用二次函数拟合主瓣,波束拟合范围分别为-20°~+20°和-30°~+30°,对应的双波束间隔角度分别为20°和30°,得到的方向图拟合系数分别为[-4.711,6.090]以及[-4.224,6.090]。由图 5可以看出:本文提出的模式滤波方法可以达到理论估计精度,估计精度随着信噪比的提高而提高,不同模式下测角精度不同,取决于模式及模式大小的乘积。除模式4由于模式大小偏小外,模式1~3、5对应的测角精度均优于传统比幅测角方法。图 5中还给出了N为6、l为4、测角模式m为4时的估计性能仿真。根据表 1,此时要求c-2=c2=0,为了便于对比,仿真天线模式参数c0~c5选择为4.067、0.437、0、0.180、0.014、0.065。可以看出,此时测角性能劣于N=180时模式4的测角性能,与理论分析给出的估计误差反比于(N)1/2一致。图5中,在SNR较低时出现的估计误差小于理论误差,是因为此时估计值被限定在[-π/4,π/4]范围内,影响了测角误差的估计。 本文提出一种基于模式滤波的旋转单天线测角方法,通过将天线方向图表示为指数和形式,设计合适的模式滤波参数,对旋转圆周上均匀观测点收到的信号的功率进行加权,实现对角度的解析估计;由于滤波得到的模式影响测角精度和测角范围,在不同观测条件下需要采用不同的模式选择方法。本文提出的方法可获得较高的测角精度,算法简单,容易实现,对天线的适应性较强。由于只需要单个接收天线和处理通道,该方法可应用于小型无人机、微纳卫星等装载能力有限、或难以布置长基线的平台,具有十分广泛的应用前景。■
3.3 模式相位φ的估计

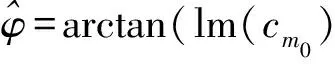
4 测角性能分析
4.1 测角范围和模糊问题
4.2 理论误差分析
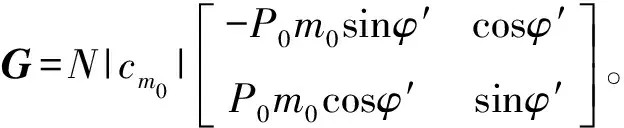
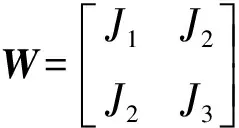
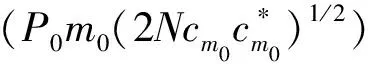
5 仿真分析
6 结束语

