基于模糊图的相位干涉仪解模糊方法

陈 璐 常 露

(航天恒星科技有限公司 西安 710100)

0 引言

相位干涉仪[1]测角方法广泛应用于遥感、雷达等系统的波达方向估计领域中[2]，其具有测角精度高、易于实现等技术特点[3]。但在高频系统中，受限于天线的物理尺寸，相位干涉仪基线长度通常大于半波长，这会导致相位差测量模糊[4]。

相位干涉仪测角方法中，相位差解模糊的正确率决定了测角精度[5]，文献[6]研究了多种相位差解模糊的方法，并讨论了各种方法的优缺点。文献[7]提出了一种基于多基线比值法的相位差解模糊方法，具有一定的工程应用价值。文献[8]提出了一种基于双频段的相位差解模糊方法，该方法不用增加基线数量，在某些体积较小的系统中具有重要实践意义。

本文将脉冲多普勒雷达距离速度模糊图[9-10]的概念推广至相位干涉仪测角系统，推导出了双基线相位干涉仪测角系统相位差模糊图的表达式，并说明了相位差解模糊余量与正确解模糊概率的关系，指出了正确解模糊的限制条件，并提出一种基于相位差模糊图的解模糊方法，该方法实现简单，可以扩展至多频多基线[11-12]相位干涉仪测角系统，为不同的相位干涉仪测角系统相位差解模糊方法提供一定的参考意义。

1 相位干涉仪测角

相位干涉仪测角系统的原理是利用基线长度为d的两个天线，接收同一目标回波信号，通过比较接收信号的相位差φ，可以得到目标的角度θ。相位差φ为[13]

(1)

其中λ为波长，通过计算可得其测角公式为

(2)

相位差测量不准会导致存在测角误差，对式(1)两边求微分并写成误差形式可得测角误差公式为

(3)

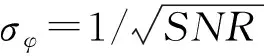
由于相位干涉仪鉴相器给出的相位差范围是(-π,π]，而实际的相位差是以2π为周期的，当d>λ/2时，会导致测角模糊[15]。图1给出了单方向最大无模糊角度与基线半波长比之间的关系。

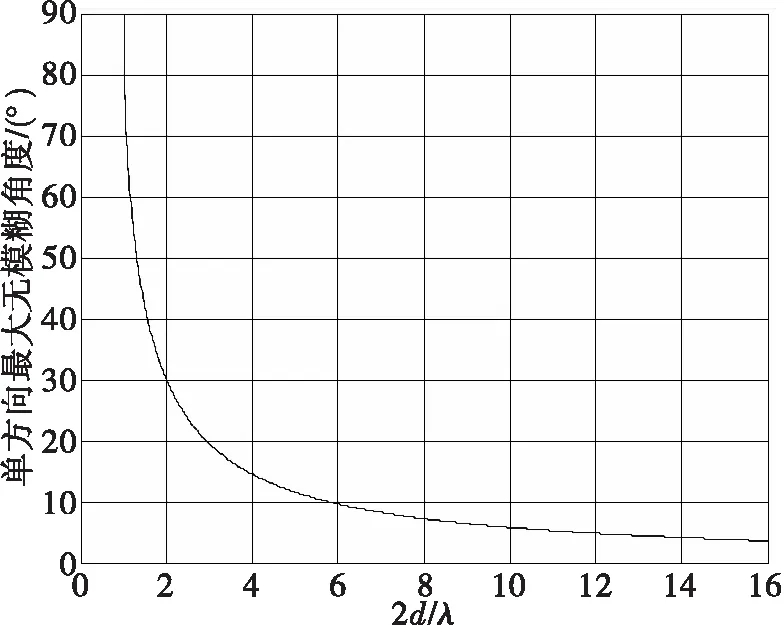
图1 最大无模糊角度与基线半波长比

图1可以看出，当基线长度d<λ/2时可以实现无模糊测角，随着基线长度增加，最大无模糊角度减小。

图2给出了当d=8λ/2时，相位差与目标角度的关系。可以看出一个相位差值对应着多个角度值。因此在测角时需要对测得的相位差值进行解模糊。

2 解模糊方法

相位干涉仪测角时基线长度d越长测角精度越高，但最大无模糊角度越小。因此通常采用长短基线相结合的方式进行相位差解模糊并进行测角[16]。而在实际应用中，当波长较短时，受天线物理尺寸限制，相位干涉仪最短基线长度很难小于半波长。图3为双基线测角系统示意图。

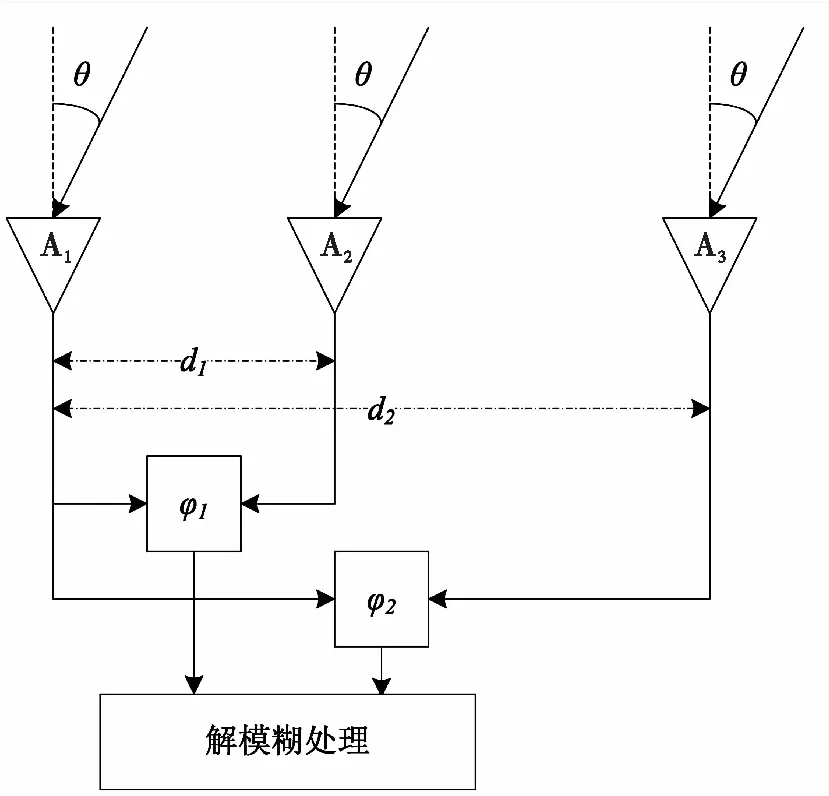
图3 双基线测角系统

双基线测角系统采用3个天线A1、A2、A3，其中A1与A2的基线长度为d1，A1与A3的基线长度为d2。两条基线测量得到的相位差分别为φ1、φ2。当不考虑测量误差时，目标角度θ为

(4)

式(4)中x1和x2分别表示在基线长度为d1和d2情况下相位模糊次数(取0, ±1, ±2, ±3, ±4, …)。重新整理式(4)可以得到

(5)

图4当d1=5λ/2、d2=8λ/2为φ2关于φ1的函数图，可以称其为双基线测角相位差模糊图[17]。各条线对应于相应的模糊次数：x1和x2。在两条基线下对目标角度无误差的测量值将对应于其中一条线上的一点。

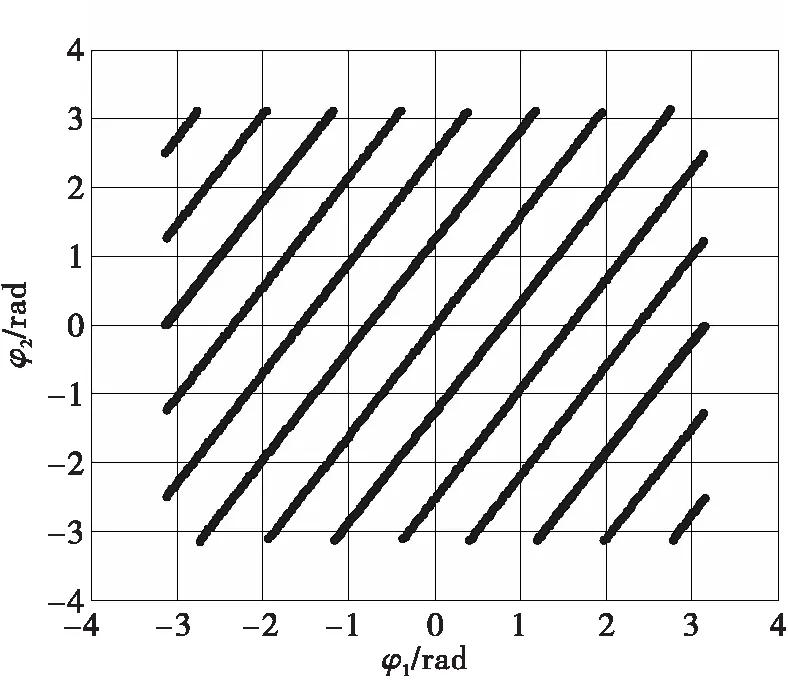
图4 双基线测角相位差模糊图

在双基线测角相位差模糊图中，x轴截距Dx和y轴截距Dy分别为

(6)

考虑到式(5)的定义域和值域都为(-π,π]，因此对于相位差模糊数x1和x2取值的约束条件为Dx≤π，Dy≤π。0点到各线的距离为

(7)

实际在相位差测量中有噪声干扰，相当于测量值偏离了模糊图中的直线，处于两条直线之间，如图5所示，点O为含有噪声干扰的相位差实际测量值在相位差模糊图中位置。

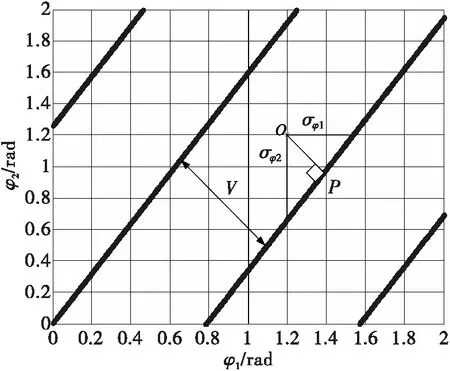
图5 相位差测量值

两条直线之间的间距V称为相位差解模糊余量。考虑到不同基线的相位差测量误差概率密度分布相同，可以令σφ1=σφ2=σφ。那么，在满足式(8)的条件时，就可以避免相位差模糊导致的测角错误。

(8)

V可以通过式(7)相邻直线相减得到。

这样可以通过求点O到最近直线的投影P点作为正确的相位差测量值。那么相位差解模糊方法可以按照下面的步骤：

1)通过系统参数得到相位差模糊图中的直线方程，即式(5)；

2)测量得到O点的坐标(Oφ1,Oφ2)；

3)利用点到直线的距离公式求出所有的OP长度，并找出最短的OPmin；

4)求出Pmin坐标(Pφ1,Pφ2)，即为无模糊的相位差值。

得到解模糊后的相位差值就可以求出目标角度θ。由式(8)可以看出相位差解模糊余量V越大，意味着相位差测量误差的容限越大，正确解模糊概率就会越高。在相位干涉仪测角系统设计时，不同参数情况下对应的相位差解模糊余量不同，应根据测角范围合理确定天线基线长度比。在一些特定情况下[18]，模糊图中的直线为等间隔的，这可以使系统设计计算更简便。在三基线相位干涉仪测角系统中，也可以通过解模糊余量来计算正确解模糊概率。

3 仿真分析

针对上述分析，我们设计相位干涉仪测角系统基线长度分别为d1=5λ/2、d2=8λ/2，测角范围-60°～+60°，输入信噪比SNR= 13 dB，按测角范围每间隔1°进行10000次随机试验，验证各角度的相位差正确解模糊概率，试验结果如图6所示。

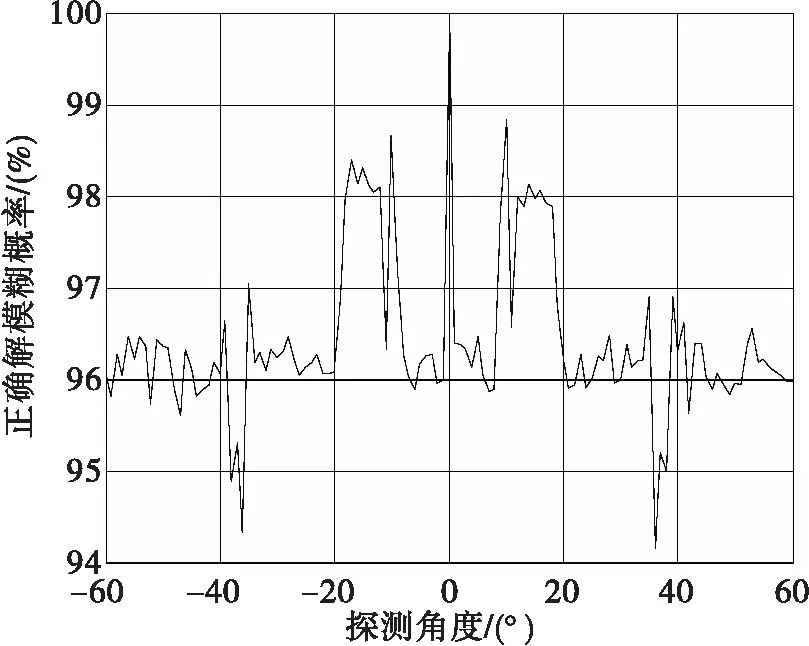
图6 探测角度与正确解模糊概率

由图6可以看出在试验设计参数情况下，正确解模糊概率可以达到94%以上。

为了验证解模糊性能，我们设计相位干涉仪测角系统参数{d1=5λ/2、d2=8λ/2}，{d1=5λ/2、d2=13λ/2}，{d1=8λ/2、d2=13λ/2}，相应的解模糊余量为V1=0.666 rad，V2=0.451 rad，V3=0.412 rad，测量某一固定角度(试验中选择35°)，在输入信噪比SNR= 5～18 dB，每隔1 dB进行10000次随机试验，试验结果如图7所示。

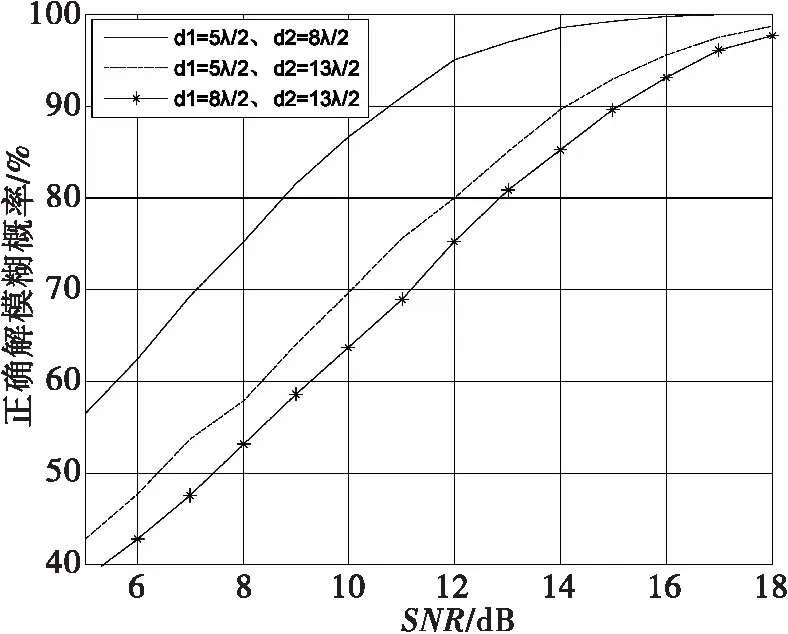
图7 信噪比与正确解模糊概率

由图7可以看出，相位差正确解模糊概率随信噪比增加而增大；在同一信噪比情况下，相位差解模糊余量越大正确解模糊概率越大。

4 结束语

当基线长度大于半波长时，相位干涉仪测角系统存在相位差测量模糊问题。本文将脉冲多普勒雷达距离速度模糊图概念推广至相位干涉仪测角系统，推导出双基线相位干涉仪测角系统相位差模糊图的表达式，并提出一种基于模糊图的相位差解模糊方法。该方法通过寻找含有噪声干扰的测量点到模糊图最近距离点得到解模糊的相位差值，并通过仿真分析验证了该方法的可行性。并指出在相位干涉仪设计时，应根据相位差解模糊余量合理确定天线基线长度比。这种方法实现简单，可以扩展至相位干涉仪多基线或多频段测角系统。