框架－剪力墙混合结构层模型试验研究＊

谢 凡，沈蒲生

（湖南大学土木工程学院，湖南长沙 410082）

高层混合结构目前在我国的地震区和非地震区的高层建筑以及超高层建筑中应用较多，国内已有不少学者对各种模型进行了振动台、拟动力以及节点等一系列研究［1－2］.显然抗震能力是研究这种结构体系的重点，基于性能的设计需要考虑结构及构件在地震荷载作用下的非线性反应，为了解混合结构的滞回特性及变形性能，制作了一组层模型试件，通过低周循环反复加载试验进行分析研究，并试图找到合适的数值模拟方法.

1 试验概况

1.1 试件设计与制作

本次试验共制作了6榀框架－剪力墙结构层模型试件（图1）.剪力墙分2种类型，整体墙和分缝墙，其中，整体墙高宽比为1.0；分缝墙是整体墙中间开20mm的缝，形成两个墙肢，每个墙肢的高宽比为2.0.框架柱分3种类型：钢柱、钢骨混凝土柱和钢筋混凝土柱，其中，钢柱采用10号热轧普通工字钢；钢骨混凝土柱的截面尺寸为100mm×115 mm，内部采用格构柱，由4个等边角钢∟25×3组成工字形，缀板宽50mm，厚5mm，采用螺栓连接；钢筋混凝土柱截面尺寸为100mm×125mm.3种柱的截面按照抗弯刚度EI基本相等的原则设计，框架柱和剪力墙的刚度比与文献［1］中的模型一致.框架梁均为钢筋混凝土梁，截面尺寸150mm×100 mm，梁柱线刚度比为0.75.每种剪力墙分别对应3种类型的柱组成6个不同形式的框架－剪力墙结构：钢筋混凝土框架－整体墙（RC－W）、钢筋混凝土框架－分缝墙（RC－SW）、钢框架－整体墙（S－W）、钢框架－分缝墙（S－SW）、劲性混凝土框架－整体墙（SRC－W）和劲性混凝土框架－分缝墙（SRC－SW）.试件材料的力学性能见表1和表2.

图1 试件尺寸及配筋图Fig.1 Size and reinforcement of the specimens

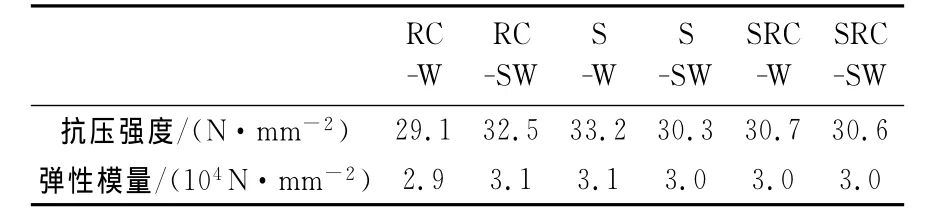
表1 混凝土的力学性能Tab.1 Mechanical properties of concrete

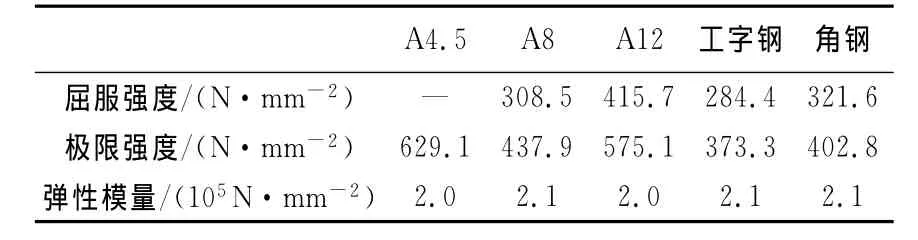
表2 钢筋及型钢的力学性能Tab.2 Mechanical properties of steel

1.2 试验装置及测试内容

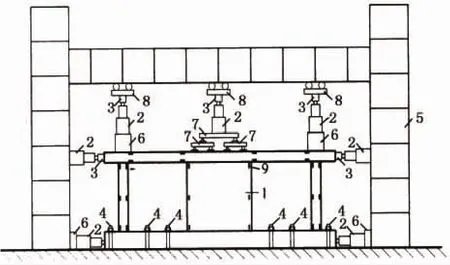
图2 试验装置图Fig.2 Experimental device

试验装置如图2所示.剪力墙顶部承受的竖向荷载采用八分点四集中荷载方式来模拟均布荷载，水平荷载由框架梁两端的千斤顶提供.在柱顶、剪力墙顶部中点以及底梁两端各布置一个位移计.剪力墙、框架柱的上下端及框架梁左右端表面两侧均布置有应变片，内部相应部位的钢筋或型钢也预埋有应变片.

加载制度：根据《建筑抗震试验方法规程》的要求［3］，先施加竖向荷载，稳定后开始施加水平荷载，全程采用位移控制加载.试件开裂前每级荷载进行1次循环，开裂后，每级荷载进行3次循环.

测试的主要内容有：试件的荷载－位移滞回曲线，钢筋、混凝土应变，试件的裂缝分布等.

2 试验描述及分析

2.1 RC－W和RC－SW

对于RC－W，经过弹性阶段后，试件开始出现受拉裂缝，出现顺序依次为：剪力墙、框架柱及框架梁.剪力墙边缘出现水平裂缝，腹部出现对角斜裂缝.腹部斜裂缝随荷载的增加进一步增多，由下至上遍布整个墙体，同时底部形成一条主水平裂缝向压区延伸.其后，剪力墙斜裂缝发展变缓，裂缝发展主要表现在底部那条主水平裂缝，不断往压区延伸，裂缝宽度开始显著增加.底部受压区出现压碎迹象，荷载也接近达到峰值.随后，框架柱底部也出现压碎迹象.在位移不断加大及反复作用下，剪力墙底部主水平裂缝的宽度不断扩大并贯通整个截面，两底角混凝土压碎，剥落.

剪力墙的破坏从破坏特征来看仍属剪弯破坏.框架柱的破坏集中在上下两端，且均被压碎，下端更为严重.框架梁在与剪力墙相连的下部和与框架柱相连的上部均出现混凝土压碎迹象，与剪力墙相连处破坏更为严重，混凝土有少量剥落，钢筋从读到的应变上看已达到受拉屈服.

RC－SW的初期裂缝的发展与RC－W类似，但剪力墙的斜裂缝开展较少，裂缝主要分布在各墙肢下半部分，各墙肢顶部竖缝两边有少量水平裂缝及斜裂缝，连接两个墙肢的顶部小连梁的裂缝开展较大.

剪力墙为典型的剪弯破坏.由于该试件框架柱的轴压比加大，柱的破坏更为严重，柱下端混凝土大量剥落，箍筋露出，纵筋被压曲外鼓.荷载达峰值后，继续加大位移，水平承载力无明显下降，试件有明显的屈服阶段，延性较好.加载到最后阶段，框架柱下端由于混凝土大量剥落，截面削弱较多，轴向承载力降低，而无法保持最初的轴压比.框架梁的破坏过程基本和上个试件相同，只是该试件的延性较好，在位移很大时，框架梁的破坏程度更严重一些.

2.2 S－W和S－SW

剪力墙和框架梁的破坏过程分别同RC－W和RC－SW相似.不同之处在于框架柱，由于是钢柱，加载到最后阶段，钢柱的外观完好，但从应变上可以看到，钢柱翼缘压应变已达屈服，拉应变尚未屈服.柱子仍有较好的轴向承载力.

2.3 SRC－W和SRC－SW

试件的破坏过程分别同RC－W和RC－SW，不同之处在于，SRC－W的柱子轴压比达到了0.5，而RC－W的柱子轴压比仅为0.2，因此加载到最后，劲性混凝土框架柱的破坏比较严重，混凝土剥落明显，箍筋外露，内部角钢被压曲，外鼓.

综合而言，无论剪力墙为整体墙或者分缝墙，加载到最后，框架柱和框架梁均达极限状态，出现压区被压碎或屈服.当框架柱为钢筋混凝土和劲性钢筋混凝土的试件时，框架柱的破坏均比较严重，混凝土出现了剥落，柱截面削弱明显，无法保持最初施加的轴压比，从而试件丧失承载力.而对于框架柱为型钢的试件，在达到同样位移的情况下，型钢的外观完好，轴向承载力并没有削弱，破坏主要表现在剪力墙上，两侧的框架对剪力墙起到了一定的支撑作用，试件的延性有所提高，相比采用钢筋混凝土柱的试件，延性要提高13%左右，劲性混凝土柱和型钢柱类似.

试验结果见表3，表中的极限位移取试件进入下降段后，荷载下降至峰值荷载的85%所对应的位移.

表3 试件基本参数及试验结果Tab.3 Basic parameters of specimens and experimental results

3 滞回特性及分析

6个试件的荷载－位移滞回曲线如图3所示.

3.1 剪力墙对滞回曲线的影响

当为整体墙时，所对应的3个试件的滞回曲线成弓形，存在捏缩效应，表明受到了剪力以及钢筋粘结滑移的影响，耗能能力一般.试件没有明显的屈服点，荷载在达到峰值荷载后，承载力下降明显，下降段较陡.

当为分缝墙时，所对应的3个试件的滞回曲线形状饱满圆滑，呈梭形，滞回环包围面积较大，表明有较强的耗能能力.试件存在明显的屈服点，进入下降段后，坡度较缓.

3.2 框架柱对滞回曲线的影响

框架柱为型钢和劲性混凝土的试件延性较好，达峰值位移后，仍有较好的变形能力，下降段相对较长，而采用钢筋混凝土的试件延性相对较差.

3.3 轴压比对滞回曲线的影响

剪力墙的轴压比的适当增加会提高承载能力，增加刚度，降低延性.框架柱的轴压比会产生与剪力墙类似的效果，但轴压比对不同类型柱的试件的延性的影响有着显著的差别，由小到大依次为型钢柱、劲性混凝土柱、钢筋混凝土柱.轴压比较大时，在反复荷载作用下，混凝土破碎，导致劲性混凝土和钢筋混凝土的截面减小，承载力降低，框架对剪力墙的支撑约束作用将会削弱，试件的延性降低.

图3 试件滞回曲线试验值及计算值比较Fig.3 Tested and computational results of the specimens

4 数值模拟

4.1 材料的本构曲线

混凝土受压应力－应变关系按照Mander建议的公式计算［4］；而受拉应力－应变曲线采用上升段线性，下降段按照混凝土结构设计规范取值.钢筋的应力－应变曲线则采用理想弹塑性模型.

4.2 梁柱单元模型

4.2.1 计算模型的选择

梁柱单元的非线性模型可分为集中塑性模型和分布塑性模型2大类，本文采用分布塑性模型.

分布塑性模型需将截面的刚度或柔度通过数值积分方式集成，因此需捕捉加载过程中各求积节点处的切线刚度或柔度.计算截面刚度或柔度的方法可分为基于塑性理论和纤维模型，本文采用纤维模型.纤维模型是将截面离散为多个纤维（弹簧），在平截面假定的条件下，得到截面在多轴作用下的弹塑性应力－应变关系［5］.

有2种方式将各求积节点的截面刚度（柔度）集成：一种是根据几何协调关系假设单元变形场的分布形式，利用虚位移原理由各截面刚度集成得到单元刚度，即刚度法；另一种是根据平衡方程假设单元力场的分布形式，利用虚力原理由各截面柔度集成得到单元柔度，即柔度法［6］.柔度法的单元柔度矩阵可表达为：

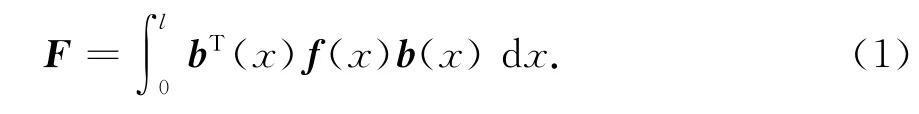
式中：b（x）为力插值函数矩阵；f（x）为切线截面柔度矩阵.

设单元长度为l，式（1）采用数值积分形式：

式中：ξi为求积节点局部坐标，ξi∈［0，l］；ωi为权系数；Np为高斯点数.

柔度法预设的力分布模式在不考虑几何非线性的条件下，在变形过程中能够严格遵守，且对一个构件只需划分一个单元就可以得到较为准确的结果，本文采用柔度法.

4.2.2 梁柱单元柔度法下降段的处理

钢筋混凝土梁柱由于混凝土应力达峰值后会出现应变软化，从而引起截面的力变形曲线出现下降段.柔度法针对下降段的处理方法如图4所示.

当受力最大的截面1达到峰值后开始进入下降段，2，3，4，5的截面将为了保持平衡关系而进入弹性卸载.此时，截面1的曲率继续增加，而其他截面的曲率减小，变形朝截面1所在的积分段集中，单元的计算模型从分布塑性模型转化为集中塑性模型.集中塑性的塑性区长度取决于截面1的权系数，与单元自身的物理特性无关，且会随着求积节点数的增加，计算结果和实际结果偏差加大［7］.

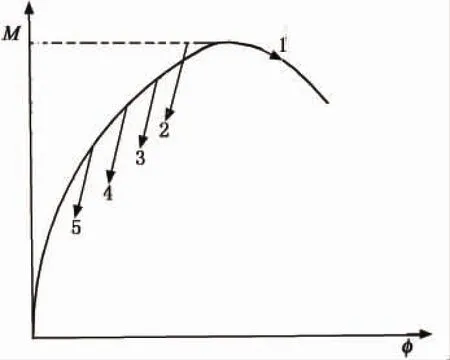
图4 弯矩曲率关系图Fig.4 Moment－curvature relation

文献［8］针对这个问题通过引入合理的塑性区长度lp，并根据lp设置数值积分方式，将单元划分为3段，中间为弹性段，两侧为弹塑性段，两侧采用两点Gauss－Radau积分，通过设定两侧单元段的长度使其边界求积节点的权系数等于lp，这样就消除了数值积分的影响.lp根据文献［9］的经验公式计算：

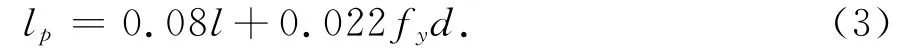
式中：l的取值按悬臂梁柱取全长，两端固支的梁柱取长度的一半；fy为钢筋屈服强度；d为钢筋直径.

但文献［8］的方法对计算模型做了较大的调整，模型更接近于集中塑形模型，降低了计算精度，限制了模型的使用范围，本文提出改进的模型.

将f（x）分解为弹性部分和塑性部分：

式中：fe（x）和fp（x）分别为截面弹性柔度矩阵和截面塑性柔度矩阵.

当某一求积节点的截面进入软化段时，设为ξ1，fp（x）除了位于ξ1的截面不为零以外，其余各求积节点的截面因进入卸载变为弹性，截面塑性柔度均为零，fp（x）变为分段函数，其一阶导数不存在，在整个积分区间对其进行数值积分已无意义，这也是前面所说增加积分点反而会令偏差加大的数学原因，因此令进入软化段的求积节点截面的权系数等于lp，lp由式（3）确定；fe（x）会因为塑形变形的累积在反复加载过程中出现刚度退化，但认为其在单元内的分布是光滑连续的，仍可采用数值积分，因此式（2）变为

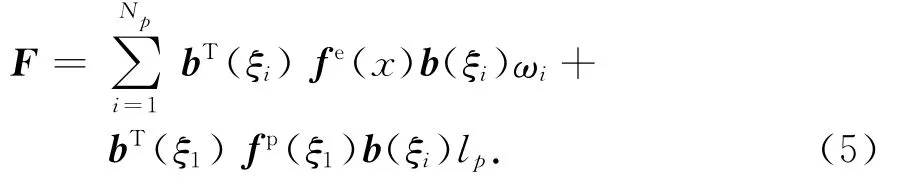
式（5）即为进入下降段的单元柔度表达式，在上升段，采用式（2）计算单元柔度.

4.3 剪力墙单元模型

无开洞剪力墙的非线性模型经过多年的研究，目前主流的可分为两类，一类是以梁柱单元为基础，考虑剪力的作用.与梁柱单元类似，可以进一步划分为基于塑性理论模型和纤维模型.不同的是，梁柱单元因剪力较小被忽略，多采用Euler－Bernoulli梁理论，剪力墙的剪力较大，除了基于Euler－Bernoulli梁理论的单元模型外，还有基于Timoshenko梁理论的单元模型，如多垂直杆单元模型就是一种基于Timoshenko梁理论的纤维模型.

另一类是采用分层壳单元，即将一个壳单元划分成很多层，通常按照钢筋、素混凝土、约束混凝土分类划分.通过有限元计算，可以得到壳单元中心层的应变和曲率.壳单元在平面内无需采用平截面假定，能够考虑剪力作用下的截面翘曲，但在平面外即厚度方向需采用平截面假定，这样就可以由中心层应变和曲率得到各钢筋和混凝土层的应变.两类单元一个重要的差别在于和其他类型单元的连接上，基于梁理论的剪力墙单元和周围的梁单元连接时，连接节点处的抗转刚度为零，因此需在墙单元内设刚性梁和周边的梁连接，而分层壳单元因采用了节点含转动自由度的膜元，则不存在这个问题，因此本文采用分层壳单元模型.

分层壳单元模型无法像梁柱单元那样可以采用柔度法，力变形曲线下降段的处理相对较为棘手.刚度法处理下降段的方法有虚加刚性弹簧法、位移控制法、弧长法等［10］，本文采用弧长法.至于结构整体力变形曲线下降段的处理同样采用弧长法.

无论是梁单元还是墙单元，均假设钢筋和混凝土在受荷变形过程中粘结良好，不会出现粘结滑移现象.不考虑钢筋和型钢的屈曲.

利用上述方法采用自编程序对6个试件进行了数值模拟，得到了顶点位移－基底剪力的包络线，如图3所示.

5 结 论

1）框架－剪力墙结构的抗侧刚度及延性主要取决于剪力墙，两侧框架能有效地延缓剪力墙的破坏，改善结构的变形能力.

2）随着位移的加大，在剪力墙达极限状态后，柱、梁均会进入极限状态，起到良好的耗能作用.

3）为了防止强震下结构的垮塌，应对框架柱的轴压比进行控制，发挥框架对剪力墙的支撑作用，避免在反复荷载作用下，框架柱过早丧失承载力.

4）3种类型的框架柱相比较，从抗震耗能的角度来看，钢柱最好，其次是劲性混凝土柱，最后是钢筋混凝土柱.

［1］ 龚炳年，郝锐坤，赵宁.钢－混凝土混合结构模型动力特性的试验研究［J］.建筑结构学报，1995，16（3）：37－43.GONG Bing－nian，HAO Rui－kun，ZHAO Ning.Experimental investigations of the dynamic characteristics of a 23－storey Steel－RC mixed structure model［J］.Journal of Building Structures，1995，16（3）：37－43.（In Chinese）

［2］ 龚治国，吕西林，卢文胜.混合结构体系高层建筑模拟地震振动台试验研究［J］.地震工程与工程振动，2004，24（4）：99－105.GONG Zhi－guo，LV Xi－lin，LU Wen－sheng.Shaking table model test of hybrid high－rise building structure［J］.Earthquake Engineering and Engineering Vibration，2004，24（4）：99－105.（In Chinese）

［3］ 中华人民共和国建设部.JGJ 101－96建筑抗震试验方法规程［S］.北京：中国建筑工业出版社，1996.Ministry of Construction of People’s Republic of China.JGJ 101－96Specification of testing methods for earthquake resistant building［S］.Beijing：China Architecture ＆Building Press，1996.（In Chinese）

［4］ MANDER J B，PRIESTLEY M J N，PARK R.Theoretical stress－strain model for confined concrete［J］.Journal of Structural Engineering，ASCE，1988，114（8）：1804－1826.

［5］ TAUCER F，SPACONE E，FILIPPOU F.Fiber beam－column model for seismic response analysis of reinforced concrete structures［R］.Berkeley：University of California，Berkeley，Earthquake Engineering Research Center，1991.

［6］ SPACONE E，CIAMPI V，FILIPPOU F C.Mixed formulation of nonlinear beam finite element［J］.Computers ＆Structures，1996，58（1）：71－83.

［7］ COLEMAN J，SPACONE E.Localization issues in forcebased frame elements［J］.Journal of Structural Engineering，ASCE，2001，127（11）：1257－1265.

［8］ SCOTT M H，FENVES G L.Plastic hinge integration methods for force－based beam－column elements［J］.Journal of Structural Engineering，ASCE，2006，132（2）：244－252.

［9］ PAULAY T，PRIESTLEY M J N.Seismic design of reinforced concrete and masonry buildings［M］.New York：Wiley，1992：141－142.

［10］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京：清华大学出版社，2005：253－259.JIANG Jian－jing，LU Xin－zheng，YE Lie－ping.Finite element analysis of concrete structures［M］.Beijing：Tsinghua University Press，2005：253－259.（In Chinese）