反平面残余应力作用下压电体界面裂尖分析＊

肖万伸，张俊兰，谢 超

（湖南大学机械与运载工程学院，湖南长沙 410082）

压电材料结构中的各种缺陷，例如：孔洞、位错、裂纹等，会影响压电材料的电弹耦合性能.由材质不同的材料加工成的双相复合材料都包含残余应力与应变.文献［1］研究了在无穷远反平面剪切和面内电场共同作用下压电材料基体中一个压电螺型位错与含界面裂纹圆形弹性夹杂的电弹耦合干涉作用.文献［2］研究了反平面均匀残余应力作用下基体包含一条界面裂纹的情况.文献［3］研究了平面非均匀残余应力作用下基体包含一条界面裂纹的情况.文［4］进一步研究了残余应力作用下同种材料微机械裂纹尖端刃型位错扩展和位错塞积问题.文［5］运用线性压电理论求解了在反平面机械载荷与面内电场耦合作用下压电体界面裂纹与螺型位错之间的相互作用问题.文［6］研究了在远端均布荷载和面内电场耦合作用下无限大压电体中螺型位错与有限裂纹之间的干涉作用问题.

反平面残余应力与压电性的耦合作用下界面裂纹问题至今仍无人研究.本文研究反平面残余应力作用下双相压电材料中裂纹尖端撕开位移及其所引起的裂纹尖端螺型位错塞积群的问题.运用复变函数方法，求出了该问题的一般解答.作为特例，当界面只含一条裂纹时，导出了反平面残余应力作用下双相材料界面裂纹问题的复势，裂纹尖端应力强度因子和电位移场强度因子，裂纹尖端撕开位移及其所引起的裂纹尖端螺型位错塞积群，以及位错塞积区等效应力强度因子和电位移等效场强度因子的解析表达式.

1 问题描述

参考文［1］，考虑极化方向沿z轴的无限大双相压电复合材料，设xOy平面为横观各向同性平面，远端无荷载作用，在界面残余应力和面内电场共同作用下，反平面位移仅与面内电场耦合，只产生沿z轴方向的位移w，应力分量τxz和τyz，电势φ，电位移Dx和Dy，并且所有变量均为x和y的函数.

反平面位移与电场耦合的本构关系是

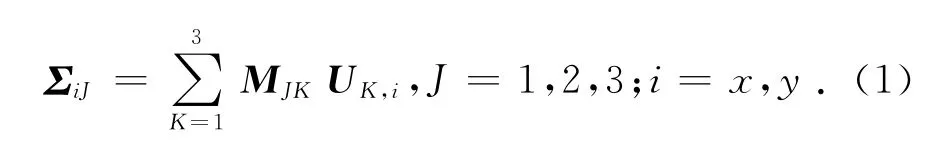
式中：广义应力、刚性系数、广义位移分别为

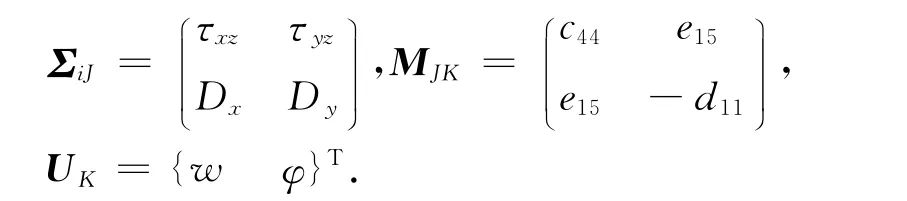
广义位移U，广义应力｛Σi｝＝｛τizDi｝T可分别用复变函数及其导数表达为：

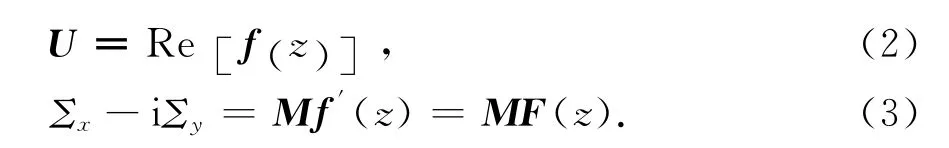
考虑如下问题：如图1所示，设压电材料电弹性模量为M1的介质Ⅰ占有上半平面S＋，电弹性模量为M2的介质Ⅱ占有下半平面S－.广义残余应力τ＝Σ0＝｛｝T作用在界面裂纹从－（g＋h）到－g和从g到（g＋h）区段上，设无穷远处受力为零.约定相应于这两种介质的量以下标1和2标记.沿实轴上有一长度为2f的绝缘裂纹L′，界面的剩余部分用L表示，rb为裂纹扩展区的长度，在裂纹扩展区产生螺型位错塞积，单个螺型位错大小用b＝｛bwbφ｝T表示.界面连接条件可以表示为：

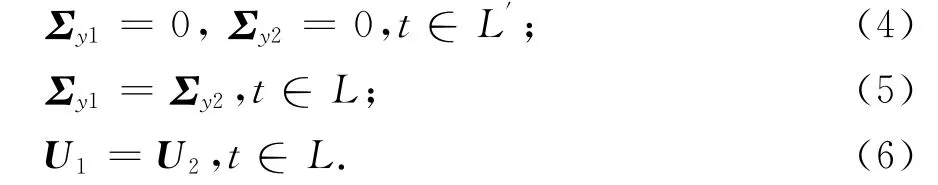
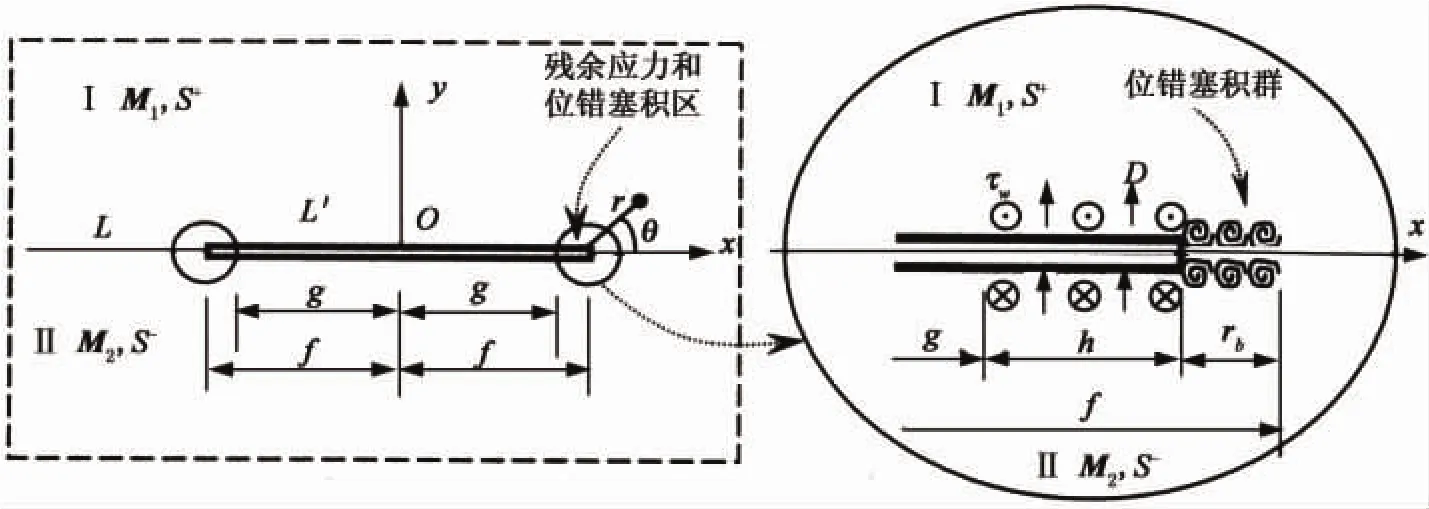
图1 反平面残余应力作用下压电体界面裂纹尖端撕开位移Fig.1 Interfacial crack－tip tearing displacement of piezoelectric materials under anti－plane residual stress

2 一般解答

当一对反平面广义集中力P位于裂纹面上时，

其复势函数按文献［1］作简化处理，得：

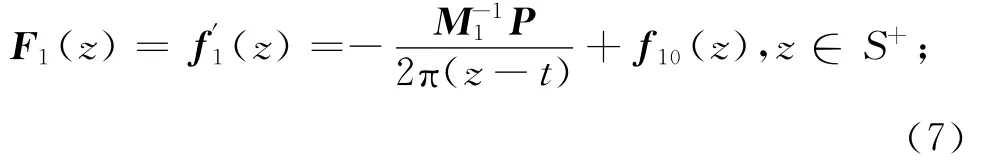
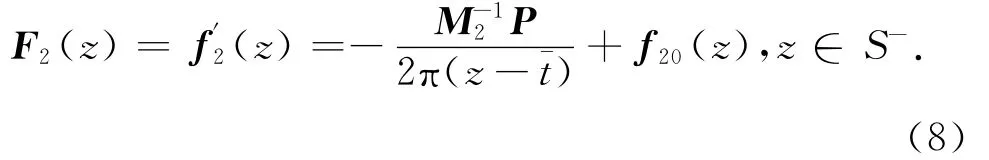
式中：f10（z），f20（z）分别在区域Ⅰ和区域Ⅱ中全纯.

由界面连接条件（4）～（6）可得到如下边值问题：

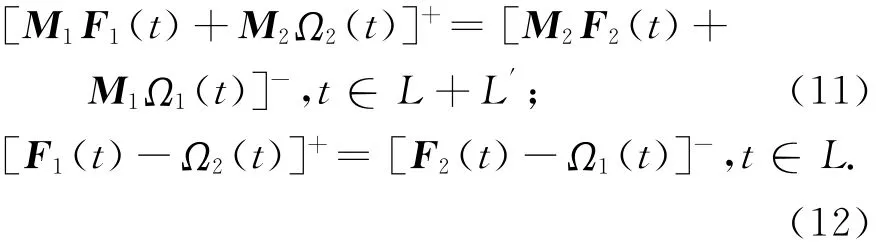
考虑式（7）～（10），对式（11）由Liouville定理可得：

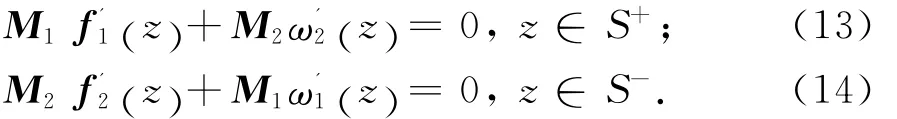
由式（12）可设

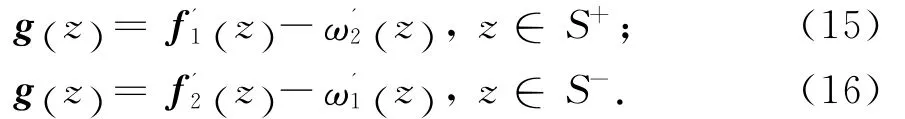
对g（z）进行奇性分析可得

式中：g0（z）在沿L′割开的全平面内全纯，在无穷远处为零.

综合以上式（13），（14），（16）和（17）可得：

将式（4）代入式（11），并注意到式（18）～（21），得

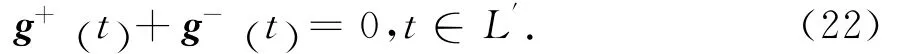
根据文献［7］中Muskelishvili理论，应用-t＝t＝x，得上述边值问题的解答

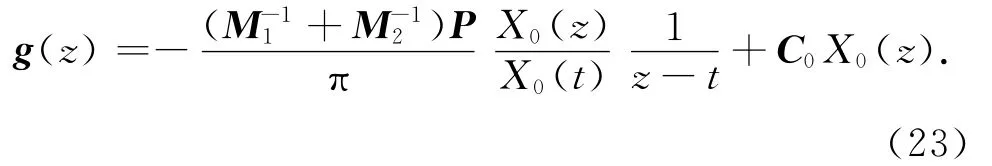
式中：

系数C0由裂纹表面应力为零条件式（4）决定.将式（4）代入式（15），（16），并考虑式（18）～（21），得∮∧g（z）dz＝0，式中∧为包围L′的围道，将式（23）代入此式可求得

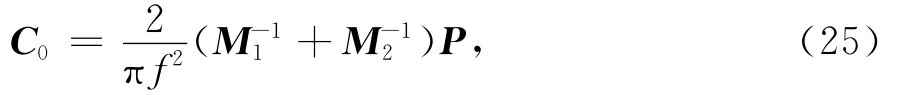
从而求得两个区域中的复势函数

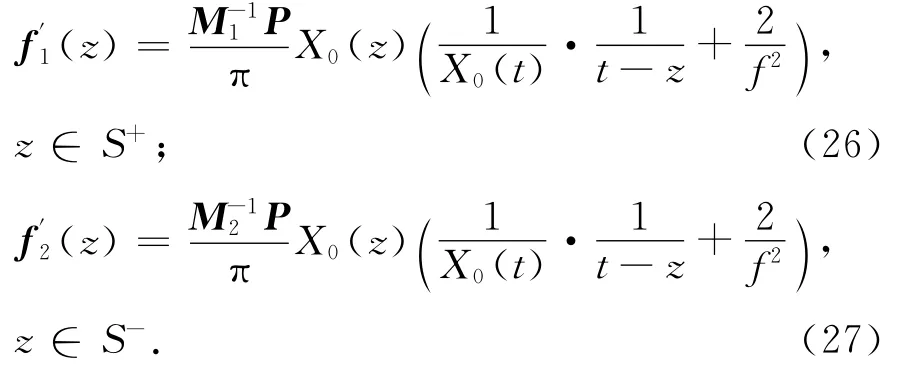
将式（26）和（27）对t从－（g＋h）到－g和g到（g＋h）积分，根据文［8］可得

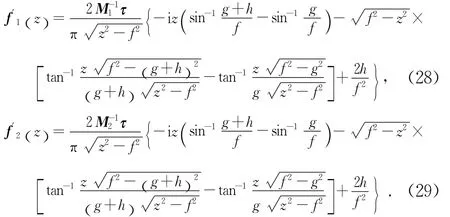
强度因子

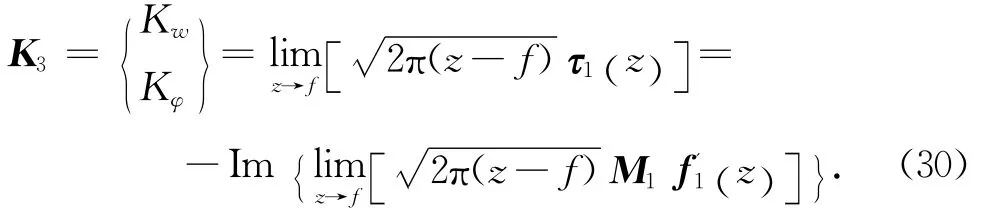
将式（28）代入式（30）得到

将式（28）和式（29）分别对z积分，得到

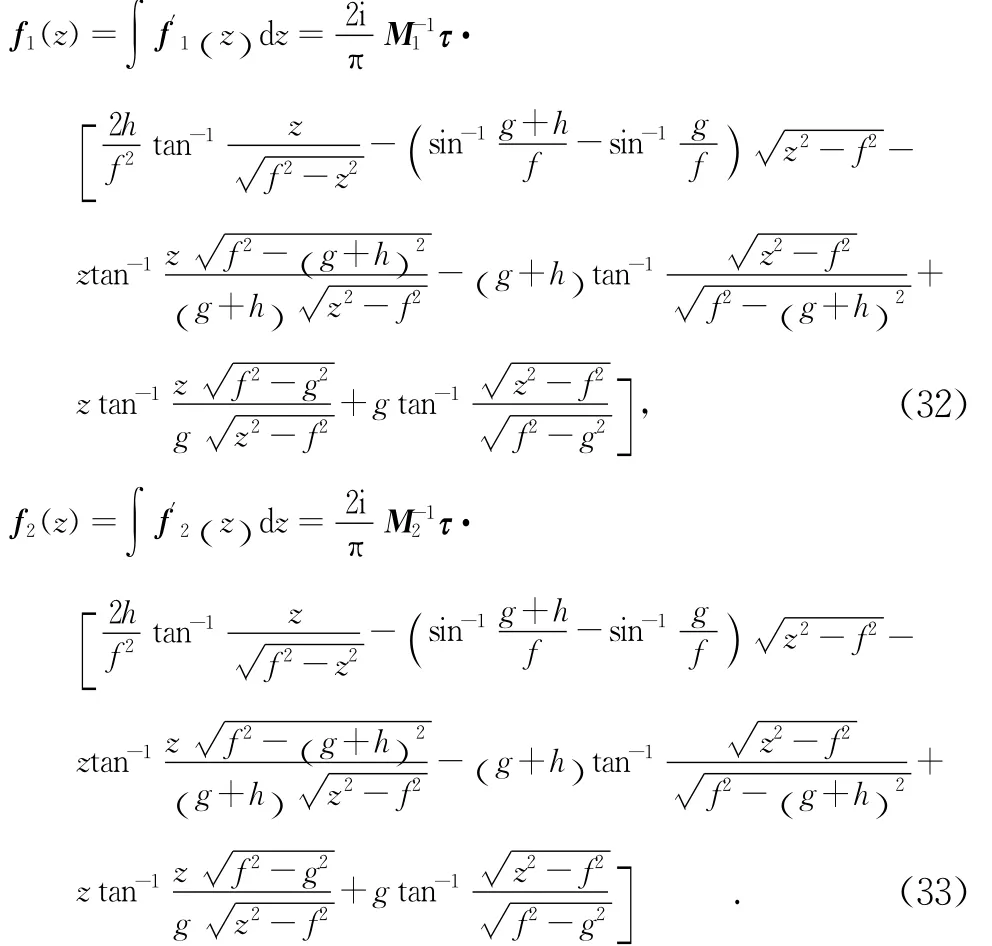
3 裂纹尖端撕开位移

裂纹尖端撕开位移

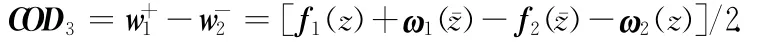
将式（32）和（33）代入上式得

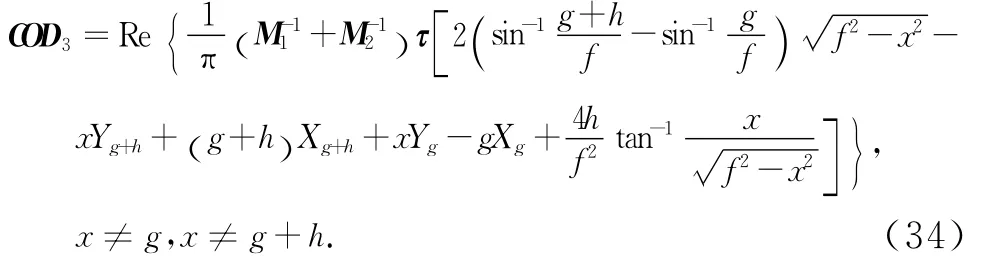
式中：

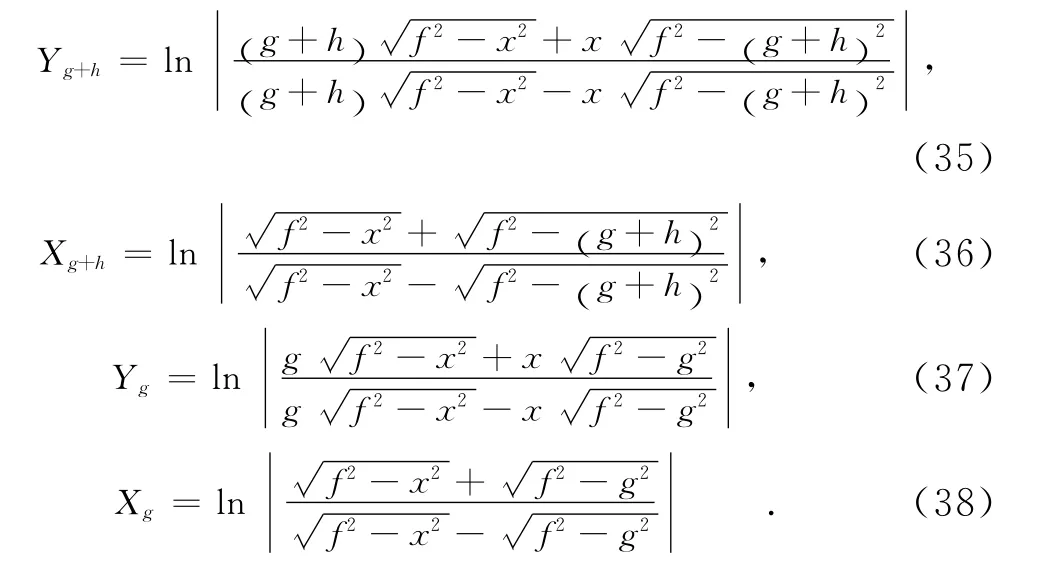
式（34）为裂纹尖端撕开位移的一般解答式，我们要对裂纹尖端点进行分析，所以要求得裂纹尖端点的撕开位移，即取x＝g＋h，代入式（34）～（38）得到

4 裂纹尖端位错塞积区位错数量

假定在位错塞积区rb力荷载残余应力和场残余应力分别产生了nw和nφ个螺型位错，那么其总的位移量应该和裂纹尖端撕开位移相等，即

由于一个螺型位错的解答可以得到多个反平面位移场，而当θ＝2π时，反平面位移量恰好等于nwbw和nφbφ，因此可得位错塞积区等效位移和等效应力强度因子如下：

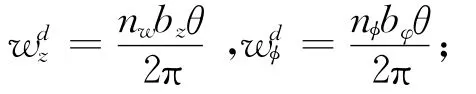
位错塞积区的等效应力强度因子和裂纹尖端应力强度因子的关系为其中α为二者之间的一个比例常数，可通过应力强度因子和等效应力强度因子求得.

5 数值分析

为了方便，取螺型位错为

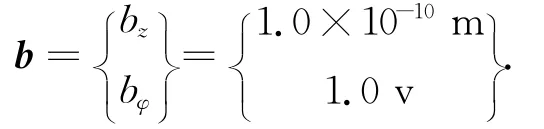
假设压电材料为PZT－6B压电陶瓷，其刚性矩阵为

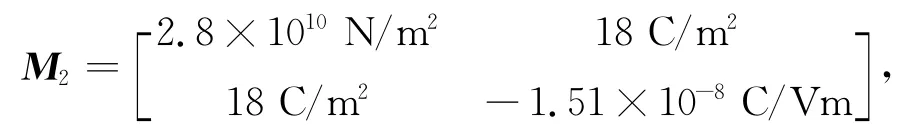
取g＝0.01m，h／g＝0.01，rb／h＝β，f＝g＋h＋βh，ζ＝c441／c442，η＝e151／e152，λ＝0.1，μ＝0.1，τ＝｛λ×c442μ×e152｝T，d111＝d112.

结合公式和已给定的数值，可得到如图2～图9的结论，下面对各个图进行分析.

如图2和图3所示，当ζ和η取上面给定的值时，力荷载作用下的裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）随着β的增加先变大达到峰值然后逐渐变小为零，而电荷载作用下的裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）达到了10－12，几乎为零，不予考虑，此处只做力荷载作用下的分析.另外，随着β的变化，当ζ＝1，η＝1时，模型退化为一种压电材料的情况，在rb＝1.4的时候，裂纹尖端撕开位移变为零，力荷载作用下的裂纹尖端螺型位错塞积群的数量同时也变为零，跟已有文献［2］相符.当η＝2不变，ζ从2变化到5时，裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）在两种材料的材料属性差异变大时随着β的增加而增加，并且随着ζ的变大，裂纹尖端撕开位移增大的幅度越来越小.

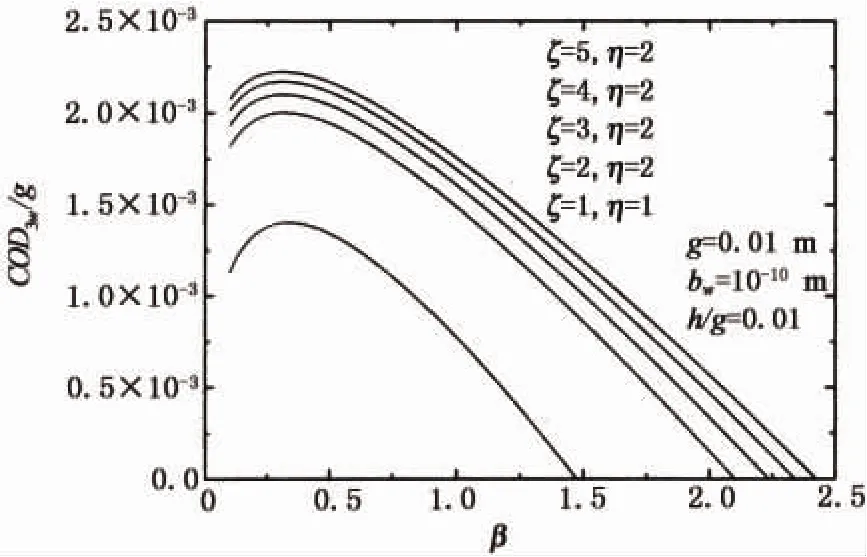
图2 力荷载作用下裂纹尖端撕开位移COD3w随着β的变化Fig.2 Variation of crack－tip tearing displacement COD3wversusβunder force load

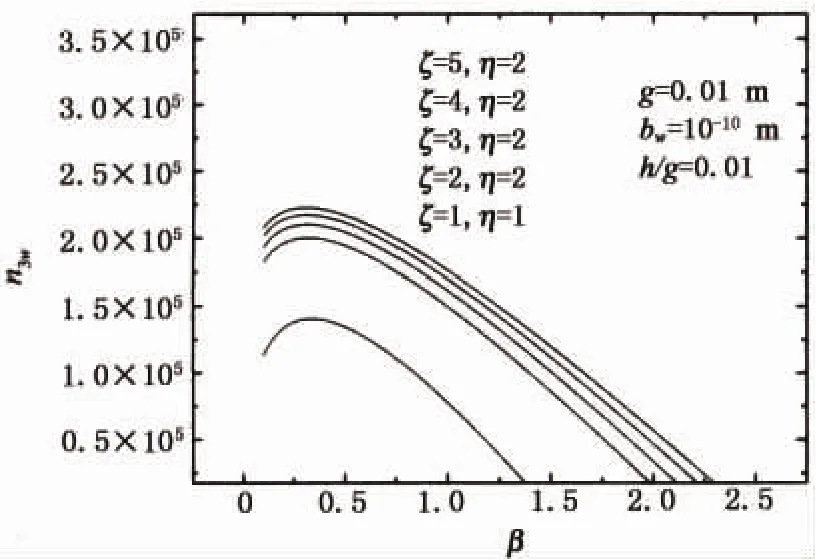
图3 力荷载作用下裂纹尖端螺位错塞积数目n3w随着β的变化Fig.3 Variation of the number n3wof the pileup screw dislocations at crack－tip versusβunder force load

如图4和5所示，当β给定时，力荷载作用下的裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）随着λ的增加而线性增加.从图中还可以看出，当β增加时，力荷载作用下的裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）随着λ的增加而减小，说明在λ一定时，β越大，在力荷载作用下的裂纹尖端撕开位移（COD3w）和裂纹尖端螺型位错塞积群的数量（n3w）反而越小.

图4 力荷载作用下裂纹尖端撕开位移COD3w随着λ的变化Fig.4 Variation of crack－tip tearing displacement COD3wversusλunder force load

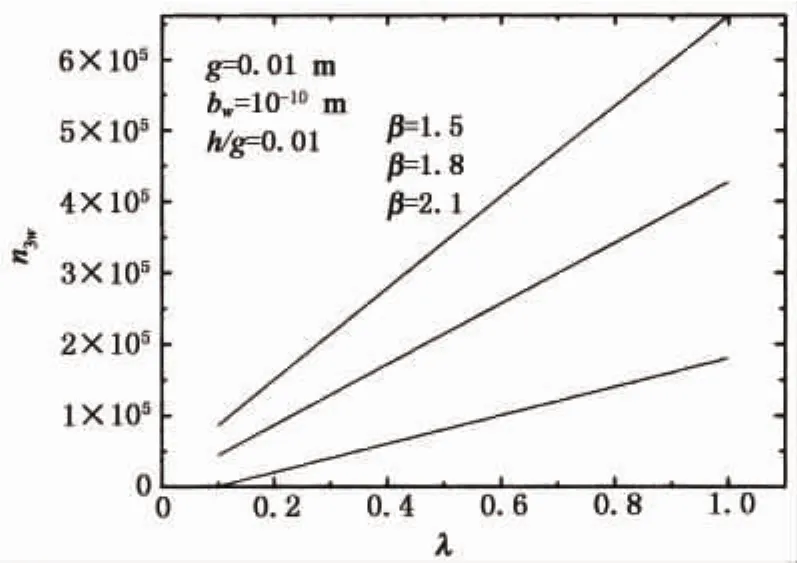
图5 力荷载作用下裂纹尖端螺位错塞积数目n3w随着λ的变化Fig.5 Variation of the number n3wof the pileup screw dislocations at crack－tip versusλunder force load

如图6所示，裂纹尖端的应力强度因子K3w随着β的增大而逐渐变小，说明在裂纹尖端，力荷载产生的螺型位错塞积群的反屏蔽效应越来越小.

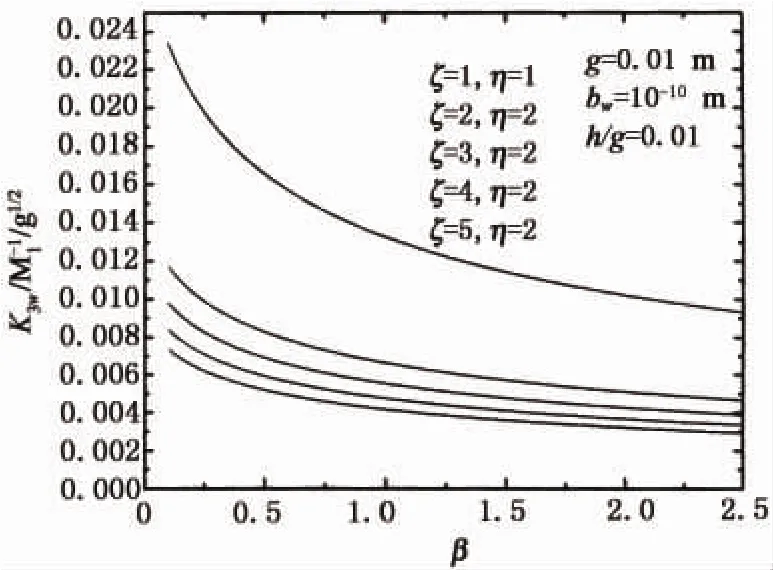
图6 裂纹尖端应力强度因子K3w随着β的变化Fig.6 Variation of crack tip stress intensity factor K3wversusβ

如图7所示，裂纹尖端的电位移场强度因子K3φ的绝对值随着β的增大而逐渐变小，说明在裂纹尖端，电荷载产生的螺型位错塞积群的屏蔽效应越来越小.

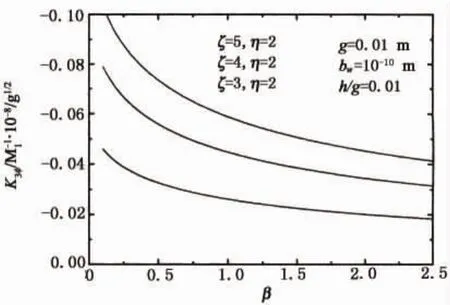
图7 裂纹尖端电位移场强度因子K3φ随着β的变化Fig.7 Variation of the electric displacement field intensity factors K3φat crack tip versusβ

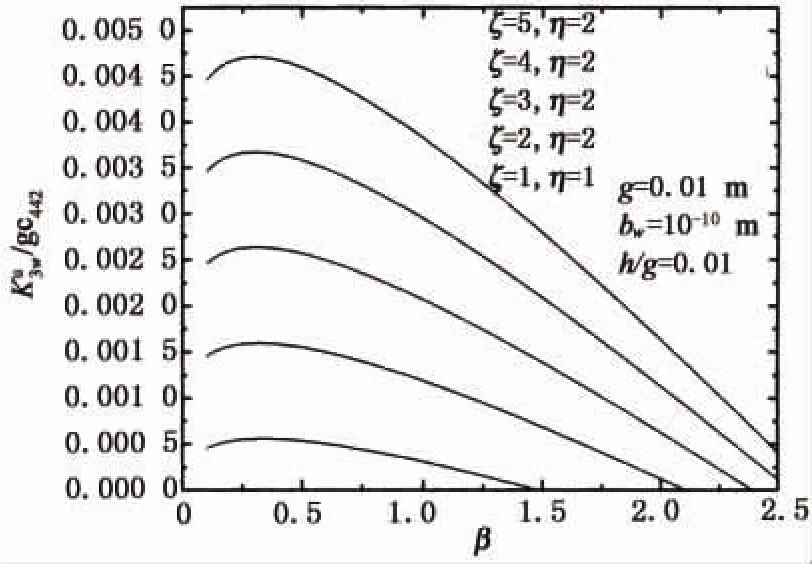
图8 位错塞积区等效应力强度因子随着β的变化Fig.8 Variation of equivalent stress intensity factor of dislocation pileup area versusβ

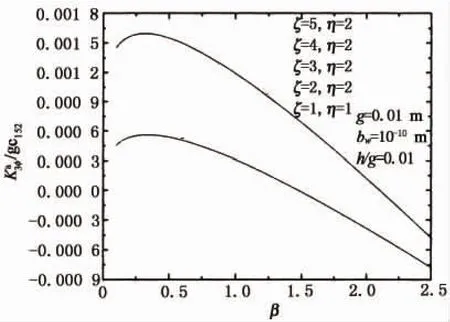
图9 位错塞积区电位移等效场强度因子随着β的变化Fig.9 Variation of equivalent electric displacement intensity factor of dislocation pileup area versusβ

6 结 论

数值结果表明，反平面残余应力对裂纹尖端撕开位移及其所引起的裂纹尖端螺型位错塞积群具有强烈的扰动效应，裂纹尖端应力强度因子对基体产生极强的反屏蔽效应.本文解答不但可用于研究残余应力对基体裂纹尖端的影响，而且可以用于研究界面裂纹和基体中任意形状裂纹的裂纹尖端撕开位移及其所引起的裂纹尖端螺型位错塞积群问题.

［1］ 刘又文，方棋洪.压电螺型位错和含界面裂纹圆形夹杂的电弹干涉效应［J］.应用数学和力学，2004，25（12）：1305－1312.LIU You－wen，FANG Qi－hong.Electroelastic interaction between a piezoelectric screw dislocation and a circular inhomogeneity with interfacial cracks［J］.Applied Mathematics and Mechanics，2004，25（12）：1305－1312.（In Chinese）

［2］ SIH G C，TANG X S.Screw dislocations generated from crack tip of self－consistent and self－equilibrated systems of residual stresses：atomic，meso and micro［J］.Theoretical and Applied Fracture Mechanics，2005，43（3）：261－307.

［3］ TANG X S，SIH G C.Edge dislocations generated from a microcrack under initial residual stress of non－uniform distribution［J］.Theoretical and Applied Fracture Mechanics，2005，44（3）：208－233.

［4］ LI L X，TANG X S，WANG Z D.A micromechanical cracking imperfection model of edge dislocations generated by residual stresses［J］.Journal of the Chinese Institute of Engineers，2008，31（3）：427－435.

［5］ WU X F，STEVE C，YURIS A D.Screw dislocation interacting with interfacial and interface cracks in piezoelectric bimaterials［J］.International Journal of Engineering Science，2003，41（7）：667－682.

［6］ CHEN B J，XIAO Z M，LIEW K M.A screw dislocation interacting with a finite crack in a piezoelectric medium［J］.International Journal of Engineering Science，2004，42（13／14）：1325－1345.

［7］ MUSKHELISHVILI N L.Some basic problems of mathematical theory of elasticity［M］.Leyden：Noord－hoff，1975.

［8］ GRADSHTEYN I S，RYZHIK I M.Table of integrals，series，and products［M］.7th ed.New York：Academic Press，1980.