基于模态柔度矩阵识别结构损伤方法研究
刘小燕,姜太新,王光辉,2
(1. 长沙理工大学土木与建筑学院,湖南 长沙410076;2. 湖南理工学院土木与建筑学院,湖南 岳阳414006)
基于模态柔度矩阵识别结构损伤方法研究
刘小燕1,姜太新1,王光辉1,2
(1. 长沙理工大学土木与建筑学院,湖南 长沙410076;2. 湖南理工学院土木与建筑学院,湖南 岳阳414006)
基于模态柔度对结构损伤的高灵敏性,采用低阶的模态参数,利用结构损伤前、后的模态柔度矩阵,计算出模态柔度改变率,并对其进行中心差分,得到模态柔度改变率曲率,作为结构损伤识别的新指标.以简支梁和四跨连续梁为例,建立有限元模型,考虑多种损伤情况,计算新指标,并与模态柔度差、模态柔度改变率、模态柔度差曲率等指标进行对比分析,证明了新指标的有效性和简便实用性.
模态参数;模态柔度矩阵;模态柔度改变率曲率;损伤识别
结构的无损检测一直是土木工程研究的热点问题,结构损伤将导致结构刚度变化,刚度改变引起结构柔度的变化.虽然高阶模态参数对结构的刚度矩阵贡献大[1],但由于实际测试中高阶模态难以准确得到,因此,利用高阶模态来评估受损结构具有局限性.与之相反,模态柔度矩阵则受低阶模态参数影响大,在工程实践中低阶模态则比较方便获得,故基于模态柔度的方法成为结构损伤识别中一类重要方法.Raghavendrachar和Aktan[1]进行了大量桥梁模态试验,发现模态柔度以及模态柔度的变化能很好地评估桥梁结构和性能;De Wolf和Zhao[2]将固有频率、模态振型和模态柔度对损伤的敏感性进行对比分析,表明模态柔度比固有频率、模态振型对损伤更敏感;Pandey和Biswas[3]研究发现柔度矩阵差比固有频率或振型对局部损伤更敏感.国内学者在利用模态柔度评估受损桥梁方面也做了大量工作,取得了有益的结果.曹晖和Friswell[4]提出了基于模态柔度曲率的损伤检测方法.李永梅等[5]提出了基于柔度差曲率的结构损伤识别方法.彭念等[6]提出了基于损伤柔度曲率矩阵的结构损伤识别方法.
然而,在结构受损不是很严重、柔度改变不大,模态振型变化不是十分明显的情况下,利用固有频率、模态柔度改变就很难评估桥梁的受损情况.鉴于此,本文提出基于模态柔度矩阵,利用模态柔度改变率曲率新指标评估受损桥梁.通过计算损伤前、损伤后模态柔度矩阵,得到模态柔度差矩阵,计算模态柔度差矩阵对角元素,与损伤的前柔度矩阵对角元素之比得到模态柔度改变率,再对其进行中心差分,最后得到模态柔度改变率曲率.通过简支梁和连续梁的有限元计算比较,来证明新指标是否更加有效.
1 模态柔度改变率曲率基本原理与计算
柔度的物理意义是单位力作用下作用点处的位移.结构的柔度矩阵可以通过其固有频率和振型,利用下式计算[2].
(1)
其中,φi为第i阶振型,ωi为第i阶固有频率.当结构受到损伤时,结构的柔度值相对于未损伤时有较大的改变,如果损伤很严重,用模态柔度差(ModalFlexibility,简称MF)指标就能判断受损位置,或者用模态柔度改变率 (RateofModalFlexibility,简称RMF)指标、模态柔度差曲率(CurvatureofModalFlexibility简称CMF)指标来判断损伤位置.如果损伤不是很严重,MF、RMF、CMF或多或少地会带来误判.如果通过模态柔度改变率对坐标进行二阶求导,即求模态柔度改变率曲率,其变化的程度将会变得更加明显.基于此,本文提出一种基于柔度矩阵的新指标:即模态柔度改变率曲率.对损伤梁进行模态分析,得到固有频率、振型、阻尼比等模态参数,进而得到损伤前、损伤后模态柔度矩阵,两者之差得到模态柔度差矩阵.然后计算模态柔度改变率,再对其进行中心差分,最后得到模态柔度改变率曲率RMFC(i).计算步骤如下:
(1)求损伤前、后结构模态柔度差矩阵
(2)
式中,Fu、Fd分别为损伤前、损伤后模态柔度矩阵,ΔF为模态柔度差矩阵.
(2)计算模态柔度改变率(RateofModalFlexibility)
模态柔度差矩阵对角元素与损伤前模态柔度矩阵对角元素之比为模态柔度改变率.其表达式为:
(3)
式中diag(ΔF)、diag(Fu)为对矩阵进行取对角元素计算.
(3)计算模态柔度改变率曲率(RateofModalFlexibilityCurvature)
将式(3)中得到的模态柔度改变率列阵进行中心差分,即得到模态柔度改变率曲率列阵RMFC,其计算过程为:
(4)
RMFC(i)与节点位置一一对应,其大小反映结构损伤后柔度差变化的快慢.当结构某个部位出现损伤时,该部位的刚度下降,柔度增加,模态柔度改变率曲率也增大.通过绘制模态柔度改变率曲率RMFC(i)随节点变化的曲线,曲线突变处即为结构损伤的位置,同时,根据曲线突变的幅度,还可定性地判断损伤的程度.
2 损伤梁结构的有限元模拟计算
实际工程结构中的损伤,如裂缝、材料性能退化,一般会引起结构刚度产生较大的变化,而对结构的质量影响较小.因此,在有限元计算中,假定结构单元损伤只降低单元刚度,而不引起单元质量的改变[7].单元的损伤通过降低弹性模量来模拟,例如,某单元损伤程度为10%,则将改单元的弹性模量设为0.9E.
本文以常用的简支梁和四跨连续梁作为损伤识别研究的模型,将其简化为平面杆系,每个节点仅考虑竖向的振动.采用有限元分析软件ANSYS分别进行结构损伤前模态、损伤后模态分析,提取结构的固有频率和模态振型,绘制基于模态柔度差曲率矩阵的RMFC(i)曲线,并与多个模态柔度指标进行对比分析.
3 简支梁损伤有限元数值模拟计算
某梁长为4m,截面尺寸为200mm×400mm,(图1、图2),将其划分为50个单元,共51个节点.弹性模量为E=3×1010Pa,容重γ=2500kN/m3,泊松比ν=0.3.考虑单点损伤和多点损伤情况,分别计算.

图1 简支梁单元划分图
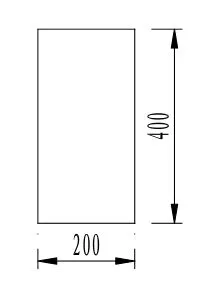
图2 截面尺寸
3.1 单点损伤识别计算分析
(a) (b)
(c) (d)
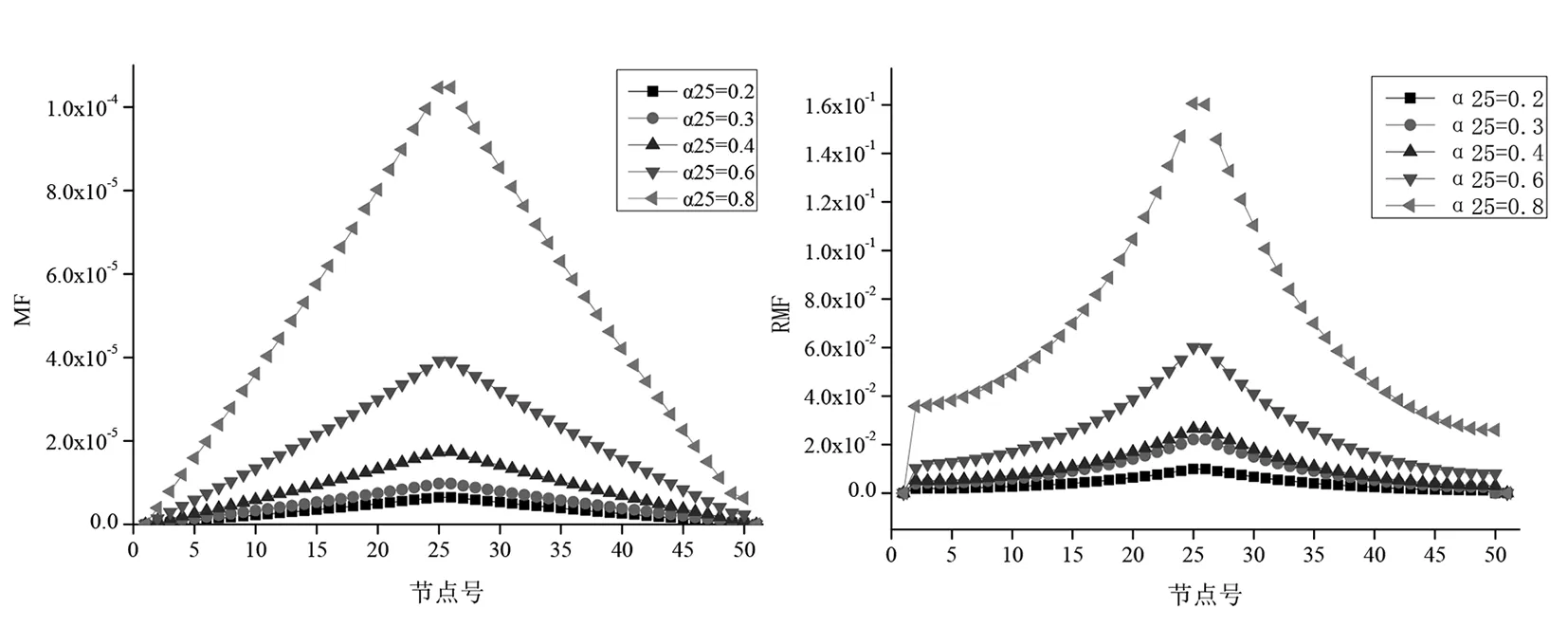
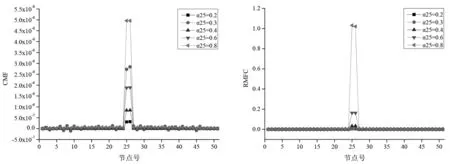
假设只有25号单元损伤,考虑损伤导致刚度下降20%,30%,40%,60%,80%共5个工况,记为α25=0.2,α25=0.3,α25=0.4,α25=0.6,α25=0.8.采用前3阶的模态参数计算得到损伤结构的模态柔度差MF、RMF、CMF和RMFC这四个指标曲线如图3所示.
由图3(a)、图3(b)可知,MF、RMF都能以最大值的方式判断出损伤单元的位置,与损伤的位置完全一致,但周边未损伤单元的指标值并不为零,这将影响对损伤单元的判断,尤其当损伤很小时.图3(c)可知,在损伤位置处,CMF法的节点指标值取得最大值,并且未损伤部分的指标值大部分趋近于零,但是损伤单元周边的单元受到影响,其指标值不规则变化.图3(d)可知,RMFC法准确的识别出损伤位置,且损伤单元周边的节点指标值都趋近于零,比CMF法更优越.而且对同一损伤程度,RMFC法的指标值比其他损伤指标大几个数量级,因此,RMFC法比其它损伤识别方法对损伤更敏感,是一种更为有效、优越的识别方法.
3.2 多点损伤识别计算分析
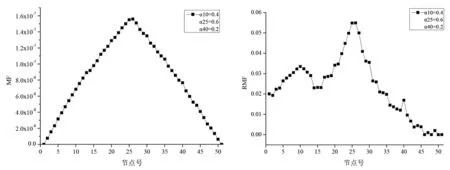
考虑3个单元损伤的情况,10号单元刚度降低40%、25号单元降低60%、40号单元降低20%,分别记为α10=0.4,α25=0.6,α40=0.2,分别计算MF、RMF、CMF、RMFC四个指标,结果如图4所示.
(a) (b)

(c) (d)
从图4(a)可以看出,MF对损伤严重的单元25可以识别出,但不太严重的单元10和单元40就很难识别.图4(b)虽然有3个峰值,但单元10跟单元40处的指标值没有明显突变,也很难判断;另外还有些地方并未损伤,但RMF指标值比损伤处的还要大,这会导致误判.从图4(c)看出3个损伤单元处有峰值,也能引导判断,但损伤单元附近的节点9的指标值比损伤单元的指标值要大,也容易引起误判.另外未损伤单元3的指标值与损伤单元40相近,会导致错判.对比发现,RMFC峰值明显,不会对附近单元产生影响,能够很好地用于损伤识别.
4 连续梁损伤有限元数值模拟计算分析
考虑一四跨连续梁,各跨跨度相等,均为4m;每跨均等分为8个单元,则共计32个单元.同样考虑单一损伤和多处损伤.单一损伤取12号单元作为损伤单元,分别考虑损伤10%、20%、40%和60%四种刚度降低情况,材料属性、截面参数均同前述的简支梁.限于篇幅,只计算在简支梁损伤识别中表现好的CMF、RMFC指标,并进行比较,结果如图5所示.
由图5(a)可知,在12号单元处,指标值达到峰值,说明CMF可以识别出损伤,但损伤单元附近的3个单元的指标值都很大,会使得判断出现误差.而模态柔度改变率曲率则消除了这一影响,从图5(b)可以看出,RMFC准确识别出损伤位置,且附近单元的损伤指标值趋于零,说明RMFC更加合理.
对于多个单元发生不同损伤程度的情况,考虑单元4、单元12、单元20和单元28刚度分别下降40%、60%、60%和40%,其指标计算结果如图6所示.

(a) (b)

(a) (b)
由图6可知,CMF依旧存在影响附近单元这一不足,对于边跨2个单元的损伤识别效果不明显.新指标则能够对连续梁的多处损伤进行准确的判断.
5 结论
本文利用结构损伤前、后的模态柔度矩阵,计算出模态柔度改变率,进一步计算得到模态柔度改变率曲率,用它作为结构损伤识别的新指标,并与模态柔度差、模态柔度改变率、模态柔度差曲率等指标进行了对比分析,以简支梁和连续梁的不同程度和不同位置的单点或者多点损伤为例进行损伤识别分析,结果表明:新指标能够更好地进行损伤识别.
[1]RaghavendracharM,AktanAE.Flexibilitybymultireferenceimpacttestingforbridgediagnostics[J].JournalofStructuralEngineering, 1992,(8):2186-2203.
[2]DewolfJT,ZhaoJ.Sensitivitystudyforvibrationalparametersusedindamagedetection[J].JournalofStructuralEngineering, 1999, (4):410-416.
[3]PandeyAK,BiswasM.Damagedetectioninstructuresusingchangesinflexibility[J].JournalofSound&Vibration, 1994, (1):3-17.
[4] 曹晖,FriswellMI. 基于模态柔度曲率的损伤检测方法[J].工程力学, 2006,(4):33-38.
[5] 李永梅,周锡元,高向宇.基于柔度差曲率矩阵的结构损伤识别方法[J].工程力学,2009,(2):188-195.
[6] 彭念,张永兴,陈建功.基于损伤柔度曲率矩阵的结构损伤识别新方法[J].工业建筑,2013,(8):15-18.
[7]CawleyP,AdamsRD.Thelocationofdefectsinstructuresfrommeasurementsofnaturalfrequencies[J].JournalofStrainAnalysis, 1979, (2): 49-57.
(责任编校:晴川)
Research on the Method of Structural Damage Detection Based on Modal Flexibility Matrix
LIU Xiaoyan1, JIANG Taixin1, WANG Guanghui1,2
(1. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha Hunan 410114, China; 2. College of Civil Engineering and Architecture, Hunan Institute of Science & Technology, Yueyang Hunan 414006, China)
Based on the high sensitivity of the change in modal flexibility to structural damage, the rate of modal flexibility curvature is presented as a new indicator for structural damage detection, derived from rate of modal flexibility calculated before damage and after damage by means of difference calculation through only a few of the lower order modes. The simply supported beam and four-span continuous beam are taken as the numerical simulation examples with considering the single damage and multiple ones. Comparing with the modal flexibility, rate of modal flexibility and curvature of modal flexibility, the results show that the new indicator is more effective and practical.
modal parameters; flexibility matrix; rate of modal flexibility curvature; damage detection
2017-03-22
国家重点基础研究发展计划(973)项目(批准号:2015CB057701);湖南省教育厅青年项目(批准号:12B056);长沙科技计划项目(批准号:k1309003-11).
刘小燕(1963— ),女,湖南桃江人,长沙理工大学土木与建筑学院教授,硕士.研究方向:钢筋混凝土基本理论、桥梁结构分析与工程控制.
U442
A
1008-4681(2017)02-0015-05

