《九章筭术》正负术“无人”辨

郭书春

(中国科学院 自然科学史研究所,北京 100190)

1 《九章筭术》正负术

《九章筭术》方程章提出了正负术,即正负数完整的加减法则。其大典本①明《永乐大典》(1408年)抄录的《九章筭经》卷 8,已佚。此据由《武英殿聚珍版丛书》本与《四库全书》本《九章算术》对校并由戴震的校勘记恢复的戴震辑录本。、杨辉本②南宋杨辉《详解九章筭法》(1261)抄录的《九章筭术》,此据《宜稼堂丛书》本并由宋景昌的《札记》恢复的原文。均作:

正负术曰:同名相除,异名相益。正无人负之,负无人正之。其异名相除,同名相益。正无人正之,负无人负之。

其中“无人”,清戴震改作“无入”[1,2]。笔者最近在《九章筭术译注》[3]中恢复了大典本、杨辉本原文,但是囿于篇幅,对几百年来在这个问题上的不同观点,没有充分展开,现进一步讨论之,以就教于方家。

《九章筭术》正负术的数学意义是明白无误的。名:名分,指称,此处即今之正负号。同名:即同号。除:这里是减的意思。前四句是正负数减法法则。“同名相除”就是相减的两个数如果符号相同,则它们的数值相减,即刘徽所说的“以赤除赤”,“以黑除黑”,则它们的数值 (这里是绝对值)相减。即“异名相益”就是相减的两个数如果符号不同,则它们的数值相加。异名:即不同号。益:增益,加。这里是说,符号不同的数相减,即以赤除黑,或以黑除赤,则它们的数值(这里是绝对值)相加。即

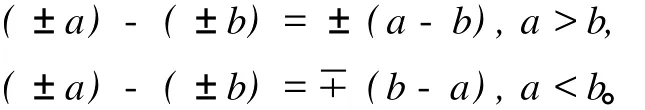
“正无人负之”是说,正数没有与之对减的数,则为负数。即

“负无人正之”是说,负数没有与之对减的数,则为正数。即

后四句是正负数加法法则。“异名相除”就是如果两者是异号的,则它们的数值(这里是绝对值)相减。即

“同名相益“就是如果相加的两者是同号的,则它们的数值(这里是绝对值)相加。即

“正无人正之”就是如果正数没有与之对加的,则为正数。即

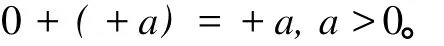
“负无人负之”就是如果负数没有与之对加的,则为负数。即

当然,关于“正无人负之”、“负无人正之”与“正无人正之”、“负无人负之”看法,学术界不尽一致。比如关于前者,钱宝琮的解释是:设b>a≥0,则b=a+(b-a),a-b=a-[a+(b-a)]=-(b-a)。在中间的式子里a和a对消,+(b-a)无可对消,改为负号,所以说“正无人负之”。

-a-(-b)=-a-[-a-(b-a)]=+(b-a)。在中间的式子里 -a和 -a对消,-(b-a)无可对消,改为正号,所以说“负无人正之”。[6]

下面将看到,钱宝琮的理解基本上与戴震一致。

2 关于“无人”的不同看法

关于“无人”,自南宋杨辉起就有不同看法。杨辉本方程章“卖牛羊”问在“一法”之“无入”下注:“古本误刻‘无人’者,非。”[7]所谓“古本”即北宋贾宪的《黄帝九章筭经细草》,它是杨辉本的底本①杨辉《详解九章筭法》实际上是为北宋贾宪《黄帝九章筭经细草》作详解,因而含有《九章筭术》本文、魏刘徽注、唐李淳风等注释、贾宪细草及其杨辉详解 5种内容。见:郭书春:《贾宪〈黄帝九章算经细草〉初探》,《自然科学史研究》Vol.7,No.4(1988.10)。。宋景昌据此认为“杨氏亦从‘入’”。钱宝琮认定戴震此处参考过《永乐大典》中所引杨辉本[8]。

1774年,戴震从《永乐大典》中辑录出《九章算术》,并加校勘,据其正本抄入《四库全书》,据其副本摆印,收入《武英殿聚珍版丛书》。戴震将正负术中的“无人”改作“无入”,并写了一个比较长的校勘记。他说:

“入”原本讹作“人”,下文及注并同。据注云“无人为无对也”,“无对”之说亦未分晓。释方程者,专为遇空位起例,而左右两行相对减,或正宜变为负,或负宜变为正,往往不得其义例。今考“同名相除,异名相异”者,如下实左右俱正,所减之余属左行,则去右行;属右行则去左行。其物品以正减正,余①此“余”,聚珍版讹作“负”,依下文及《四库全书》本校正。在所去之行,为“正无入”;以负减负,余在所去之行,为“负无入”。以正从负为“正无入”,以负从正为“负无入”。负对空位而负数在所去之行,与以负减负同例。正对空位而正数在所去之行,与以正从负同例。此皆所谓“正无入负之,负无入正之”也。“异名相除,同名相益”者,如下实左右俱正,并为一数,则无分于左右。其物品以负减正,余或左或右,为“正无入”;以正减负,余或左或右,为“负无入”。以正从正为“正无入”,以负从负为“负无入”。正对空位,与以负减正同例。负对空位,与以负从负同例。此皆所谓“正无人正之,负无人负之”也。由是言之,在所去之行则其数无入,而或左或右,以与无分于左右,合为一行。因亦谓之“无人”。“人”字乃传写之误,明矣。今悉改正。[1,2]显然,戴震反对刘徽的“无人为无对”之说,在将“人”改作“入”之后,认为“正无入负之,负无入正之”与“正无人正之,负无人负之”分别是附属于它们前面两句话的,是分别处理“同名相除,异名相异”与“异名相除,同名相益”的结果的,而不是分别独立于前面两句,处理 0-(±a)=∓a,a>0与 0+(±a)=±a,a>0的情形的。此后不久,汪莱、李潢就对戴震的改动提出异议。汪莱说:

“无人”,“人”不误。“无人”谓有空位也。“异名相益”,并右行于左行,则右行空。并左行于右行,则左行空。右行之正亦已无也,故负之。右行之负并于左行之正,左行本无负也,右行之负亦已无也,故正之。左并右亦然。“同名相除”,余在右行,而正正矣。若改归左行,左行本空位,无正也,而右行之正亦已无,故负之。余在右行,而负负矣。若改归左行,左行本无空位,无负也,而右行之空位亦已无,故正之。余在左亦然。正负者,物也,人物通称耳。[9]

显然,汪莱尽管不同意戴震将“人”改作“入”,但仍与戴震一样,将“正无入负之,负无入正之”与“正无人正之,负无人负之”分别看成是附属于它们前面两句话的。他承认“无人”就是有空位,但是这种“空位”是由“异名相益”或“同名相除”产生的。李潢按云:

“无人”之“人”字原本作“人”,孔刻改为“入”,非是。

李潢以孔刻本②孔刻本通常称为微波榭本,是孔继涵于 1777年或其后在微波榭刊刻的戴震重校的《九章算术》。戴震在此本中将自己的大量校勘冒充原文,并作了若干修辞加工。孔继涵又将此戴震校本冒充北宋秘书省刻本的翻刻本,并将刻书时间提前到乾隆三十八年(1773年)。上海古籍出版社 1990年影印了微波榭本。为底本,因此,他“于经、注作‘入’,仍孔刻也”。而在自己撰写的“说”中“作‘人’,遵原本也”。李潢说曰:

云“正无人负之,负无人正之”者,此条“同名相除”为例,正宜消正,今减行无正,则以正夺其位而为负;负宜消负,今减行无负,则以负夺其位而为正。云“正无人正之,负无人负之”者,此条“异名相除”为例,正宜消负,今减行无负,则以正夺其位而

为正;负宜消正,今减行无正,则以负夺其位而为负。“人”为相对也。减行直空位为

无对;或减行之数不足减,反减之,亦为无对,皆使消夺者居其位也。[10]

李潢将“无人”理解成“无对”,既认为减行中的空位为无对,又将减行中之不足减为无对。这与刘徽对“无对”的理解基本一致。

然而,汪莱、李潢的看法未引起后人的重视,自 1963年的钱校本[11],到 2004年的汇校本增补版[12],40余年间的各家校勘本均从戴校。

3 “无人 ”辨

正负术中的“无人”就是“无偶”,“无对”。人:偶,伴侣。《庄子·大宗师》:“彼方且与造物者为人,而游乎天地之一气。”《庄子·应帝王》:“予方将与造物者为人。”《庄子·天运》:“丘不与化为人。”郭庆藩集释引王引之云:“人,偶也。为人,犹言为偶。”[13]郭象关于这几处“为人”的解释都是错误的。《淮南子·齐俗》云:“上与神明为友,下与造化为人。”[14]“为人”亦训“为偶”。因此,《九章筭术》正负术中的“无人”不误。戴震认为“无人”系传写之误,改作“无入”,是师心自用。刘徽说:“无人,为无对也。”完全符合“无人”的本义。戴震没有理解“无人”的涵义,指责刘徽关于“无人”的解释,是没有道理的。这就是《九章筭术译注》恢复大典本、杨辉本原文的根据。

刘徽说:在“无人”的情况下,“无所得减,则使消夺者居位也”,也就是 (1)、(2)式。

“无人”为“无对”。但是,在刘徽看来,不同符号的数也是“无对”。他说:“其异名者,非其类也。非其类者,犹无对也。”李潢关于“无人”的理解含有空位与不足减两种意义的论述,接近刘徽的思想。而戴震、汪莱、钱宝琮的理解都有失偏颇。

1 (清)戴震整理.九章算术[M].乾隆御览《武英殿聚珍版丛书》本.中国科学技术典籍通汇·数学卷[Z].第 1册.郑州:河南教育出版社,1993.79—214.

2 (清)戴震整理.九章算术[M].四库全书 (文渊阁本)[Z].台北:商务印书馆,1986.

3 郭书春.九章筭术译注[M].上海:上海古籍出版社,2009.332—338.

4 郭书春.古代世界数学泰斗刘徽[M].济南:山东科学技术出版社,1992.39—40.

5 郭书春.古代世界数学泰斗刘徽 (修订本)[M].台北:明文书局,1995.36—38.

6 钱宝琮主编.中国数学史[M].李俨钱宝琮科学史全集[Z].第 5卷.沈阳:辽宁教育出版社,1998.60—61.

7 (南宋)杨辉.详解九章算法[M].宜稼堂丛书[Z].(清)道光二十年 (1842).

8 钱宝琮.戴震算学天文著作考[J].李俨钱宝琮科学史全集[Z].第 9卷.沈阳:辽宁教育出版社,1998.143—167.

9 (清)汪莱.校正《九章算术》及戴氏订讹[M].衡斋遗书[Z].1892.

10 (清)李潢.九章算术细草图说[M].中国科学技术典籍通汇·数学卷[Z].第 4册.郑州:河南教育出版社,1993年.1149—1152.

11 钱宝琮校点.九章算术[M].钱宝琮校点.算经十书[Z],上册.李俨钱宝琮科学史全集[Z].第 4卷.沈阳:辽宁教育出版社,1998.177—178.

12 郭书春汇校.九章筭术(增补版)[M].沈阳:辽宁教育出版社.台北:台湾九章出版社.2004.356—357.

13 (清)郭庆藩.庄子集释[M].北京:中华书局,1961.

14 何宁.淮南子集释[M].北京:中华书局,1998.