有限集的排列构成的格

梁菊先,钟裕林

(1.河北北方学院理学院,河北张家口075000;2.海南软件职业技术学院,海南琼海571400)

1 引 言

本文沿用文献 [1-3]中的术语和符号.在文献 [3]中给出了有限集合的所有子集作成的格及其特征多项式.在文献 [1]和 [2]对子空间轨道生成的格进行了详细的讨论.得出一些重要结果.本文采用文献 [1]中讨论问题的方法,给出了有限集的所有排列作成的格,讨论了它们的包含关系,给出格中元素的刻画及它的特征多项式.

设 P是一个非空集,≤是定义在 P上的一个二元关系.如果下列的三条公理P01-P03成立,P就叫做一个偏序集,≤就叫做 P上的偏序.

P01对于任意 x∈P,都有 x≤x.

P02对于任意 x,y∈P,如果 x≤y,而且 y≤x,那么 x=y.

P03对于任意 x,y,z∈P,如果 x≤y,而且 y≤z,那么 x≤z.

P上的偏序≤有时记作≥,如果 x≤y,而 x≠y,就记 x＜y(或 y＞x).

设 P是一个偏序集,a,b∈P,a＜b,如果不存在c∈P,使得 a＜c＜b.则称b是a的覆盖,记作 a＜·b.P中的元素m叫做 P的一个极小 (大)元,如果不存在 x∈P,使得 x＜m(x＞m).如果对所有x∈P,都有 m＞x(m＜x),则 m叫做 P的最大 (小)元.P中唯一的最大 (小)元记作1(0).

对于 x,y∈P,x＜y.如果存在 x=x0,x1,…,xn=y,使得

把 (1)叫做以 x为起点,y为终点的链,也叫 x,y链,而 n叫做它的长.如果 xi＜·xi+1(i=0,1,…,n-1),(1)就叫做 x,y的极大链.如果

也是 x,y的链.而 Xi(1≤i≤n)都在 (2)中出现,则 (2)就叫做 (1)的加细.设 P是包含0的偏序集,如果0,a链都可加细成极大链,并且所有极大链有相同的长,就把这相同的长记作r(a).

定义1 设 P是包含0的偏序集,0是非负整数所成的集合.函数 r∶P→0;a叫 P上的秩函数.如果下面的 (i)和 (ii)成立.

(i)r(0) =0

(ii)对于 a,b∈P,而 a＜·b,那么 r(b) =r(a) +1.

设 T是偏序集的一个子集,u∈P,如果对所有 x∈T都有u≥x(≤x),u就叫做 T的一个上 (下)界,如果 u是 T的一个上界,而对 T的任一个上界v,都有 v≥u,那么 u就叫做 T上确界.同样可以定义下确界.

偏序集L称为格,如果L中任意两个元素都有上确界和下确界.把L中元素a和b的上确界和下确界分别记为a∨b和a∧b,分别读作 a并b和a交b.当格L含有有限个元素时,就称为有限格.

设L是包含0的偏序集.覆盖0的元素称为L的原子,包含0的格称为原子格,如果对每个 a∈L{0},a都是L中一些原子的上确界,即

定义2 设L是包含0的有限格,L叫做几何格,如果满足以下的条件:

(i)L是一个原子格;

(ii)L具有秩函数r,而且对所有的 x,y∈L,都有

定义3 设 P是有限偏序集,K是特征数为0的域,并且μ(x,y)是定义在 P上而在 K中取值的二元函数.假定μ(x,y)满足以下三个条件:

(i)对任意 x∈P,总有μ(x,x) =1;

(ii)对于 x,y∈P,如果 x∈y,则μ (x,y) =0;

(iii)对于 x,y∈P,如果 x＜y,则∑x≤z≤yμ(x,z) =0,就把μ (x,y)叫做 P上而在 K中取值的Möbius函数.

定义4 设 P是包含0和1的有限偏序集,并且 P上有秩函数r和Möbius函数μ,那么多项式

叫做 P上的特征多项式.

2 n元有序集的排列作成的格

设A (n)={1,2,…,n}是n个元素的一个全序集 (其序按自然数的大小顺序),是 A (n)的 k元排列 (i1,i2,…,ik),k=0,1,2,…,n,记为Ak.约定0元排列A0是空集ø.A (n)的n元排列共有n!个,Ak= {i1,i2,…,ik}的的子排列Al指的是Ak的一个子集,并且按Ak的序得到A (n)的一个排列 (ji,j2, …,jl),记为 {ji,j2, …,jl} ⊂ {i1,i2, …,ik},即Al⊂Ak.

令￡(A (n))是以An的所有k(k=0,1,2,…,n)元排列为元素组成的集合,对于 Ak,Al∈￡ (A (n)),如果Ak⊃Al,就定义 Al≤Ak.那么≤是￡ (A (n))的一个偏序关系,￡ (A (n))是一个有限偏序集,并且ø和A (n)分别是它的最大元和最小元.对于 Ak,Al∈￡(A (n)),定义 Ak∩Al是它们公共元按A (n)的序所成的排列,Ak∪Al是Ak和Al中元的并按A (n)的序所成的排列.显然,Ak∩Al,Ak∪Al∈￡ (A (n)).再定义 Ak∨Al=Ak∩Al,Ak∧Al=Ak∪Al,那么￡ (A (n))对于所定义的∨和∧封闭.因而作成一个有限格,记为￡R(A (n)),称为 A (n)的排列按反包含关系生成的格.

3 重要结果

引理1 设A (n) = {1,2,…,n}是n个元素 (简称 n元)的全序集,￡R(A (n))是由A (n)的排列按反包含关系生成的格,那么|￡R(A (n)) |=

证明 因为A (n)的 k元排列Ak的个数是n(n-1) … (n-k+1),k=0,1,…,n,而￡R(A(n))是由A (n)的所有排列组合的集合,所以|￡R(A (n)) |=1+n+n(n-1) +…+n(n-1)…(n-k+1) +n!而n(n-1) …(n-k+1)因此|￡R(A (n)) |=

定理2 n＞1,X∈￡R(A (n)).定义

那么 r′∶￡R(A (n)) →0是格￡R(A (n))的秩函数,并且￡R(A (n))是几何格.

证明 前面已给出的￡R(A (n))是一个格.现在证明 (3)是￡R(A (n))的秩函数.显然,r(A (n)) =0.令 X,Y∈￡R(A (n)),X＜·Y,而 X= (i1,i2,…,ik),Y= (j1,j2,…,jl),那么 Y是 X的子排列,|X|=|Y|+1.由 (3),有 r′(Y) =n- (k-1) =n-k+1,r′(X) =nk.所以 r′(Y) =r′(X) +1.因此 r′是格￡R(A (n))的秩函数.

下面证明 ￡R(A(n))的几何性.令{^i}=A(n) {i},i=1,2,…,n,那么(1^),(2^,…,(^n)是 ￡R(A(n))的原子,∀X∈￡(A(n)),记=(i,i,…,i),那么=(i)∪(i)∪…∪(i),因而 X=∩…∩(^i)R12l12ll因此 ,在 ￡(A(n))中(i)成立.R

设 X,Y∈￡R(A (n)),当≠A (n),Y≠A (n)时,令 X= (i1,i2,…,ik),Y= (j1,j2,…,jl),那么 r′(X) =n-k,r′(Y) =n-l,因为 X∩Y是 (1,2,…,n)包含在 X,Y中元数最多的t元排列 (h1,h2,…,ht),而 X∪Y是 (1,2,…,n)包含 X,Y中元数最少的 p元排列 (m1,m2,…,mp),所以 p=k+l-t,因而|X∪Y|=|X|+|Y|-|X∩Y|,|X∨Y|=|X|+|Y|-|X∧Y|.由 (3)式,有 r′(X∨Y) =n-|X∨Y|,r′(X∧Y) =n-|X∧Y|.所以

当 X=Y=A(n)时,显然 r′(X∨Y)+r′(X∧Y)=r‘(X)+r‘(Y);当 X,Y中有一个是A(n),不妨设 X=A(n).Y≠A(n),那么 X∨Y=Y,X∧Y=X,因而 (4)成立.因此,在￡R(A(n))中 (ii)成立.

综上所述,￡R(A (n))是几何格.

定理3 设 n＞1,那么￡R(A (n))的特征多项式是

证明 因为ø和A(n)分别是￡R(A(n))的最大元和最小元.设 X,Y∈￡R(A(n)),定义

断言(5)是 ￡R(A(n))的 Möbius函数.实际上,μ(X,X)=1;并且 XY时,μ(X,Y)=0;当|X|-|Y|=t时,如果 X＜Z≤Y,而|X|-|Z|=i,那么 Z的选取个数是,而μ(X,Z)=(-1)所以

因此上述的断言成立.

由特征多项式的定义,对于 X,X′∈￡R(A (n)),如果|X|=|X′|=m,0≤m≤n,那么=tm. 因为 A (n) 含 m 个元的排列的个数是而μ (A (n),

定理4 设 M(A(m,n))={X∈￡(A(n))||X|=m},1≤m≤n-1.由 M(A(m,n))中元素的交组成的集合记为￡(A (m,n)),并且约定A (n)是M(A (m,n))中零元素的交,如果按￡R(A (n))的偏序关系来规定￡(A(m,n))的偏序,即对于 X,Y∈￡(A(m,n)),如果Y是X的子排列,就规定 X≤Y,那么￡ (A (m,n))是一个有限格,记为￡R(A (m,n)).

证明 显然|￡R(A(m,n))|＜∞,并且对于￡R(A (n))的偏序≤来说,￡R(A (m,n))是一个偏序集,而∩X∈￡R(A(m,n))X和A (n)分别是它的最大元和最小元,现在证明按照￡R(A (n))所定义的交和并是封闭的.任取 X1,X2∈￡R(A (m,n)).由 X1和 X2是 M(A (m,n))中元素的交,可知X1∨X2=X1∩X2∈￡R(A (m,n)).因为 X1∪X2⊂A (n),而 A (n) ∈￡R(A (m,n)),并且￡R(A (m,n))中包含 X1∪X2的元素的交也包含 X1∪X2,所以￡R(A (m,n))中有唯一包含 X1∪X2的最小者,因此 X1∧X2=∩{Z∈￡R(A (m,n)) |X1∪X2⊂Z} ∈￡R(A (m,n)).于是￡R(A(m,n))是一个有限格.

定理5 设 n≥m≥0.

的充分必要条件是m≥m1≥0.

证明 充分性.当n=1时,显然 (6)成立.下面假设 n≥2.我们来证明

设 P∈M (m-1,n),P= (i1,i2,…,im-1).把A (n)中的元素添加到 P中,使得 (jt0,1,it0,2, …,jt0,t0,i1,jt1,1,jt1,2,…,jt1,t1,i2,…,im-1,jtm-1,1,jtm-1,2,…,jtm-1,tm-1) = (1,2,…,n),其中{jtk,1,jtk,2, …,jtk,tk},k=0,1,2, …,m-1,有可能是空集,因为n-m≥2,所以￡R(A (m,n))中有两个不相同的子排列 P∪ (jtp,k)和 P∪ (jtq,h),jtp,k≠jtq,h},使得 P= (P∪ (jtp,k)) ∩ (P∪(jtq,h)) ∈￡R(A (m,n)),其中 k,h∈{1,2, …,l},l=t0,t1, …,tm-1,ip,iq∈{i0,i1, …,im-1}.因此 (8)成立,从而 (7)成立.

现在来证明 (6).当m=m1时,显然 (6)成立.下设 m＞m1.由 (7),可得￡R(A (m,n)) ⊃￡R(A (m-1,n)) ⊃…⊃￡R(A (m1,n)).因此 (6)成立.

必要性.由M (A (m1,n)) ⊂￡R(A (m1,n)) ⊂￡R(A (m,n)),可知￡R(A (m,n))含A(n)的m1元排列Q,并且Q是M (A (m,n))中元素的交,所以在￡R(A(m,n))中存在A(n)的m元排列 P,使得 P⊃Q,因此 m≥m1≥0.

定理6 设 n＞m≤0.那么￡R(A(m,n))由 A(n)和 A(n)的元数≤m的全体排列组成.

证明 由￡R(A(m,n))的定义,A(n)∈￡R(A(m,n)).因为￡R(A(m,n)) {A(n)}中的元素是 A(n)的含m个元的排列的交,所以对于 X∈￡(A(m,n)) {A(n)},有|X|≤m.

反之,设 P是A (n)的 k元排列,0≤k≤m,那么 P∈M(A(k,n))⊂￡R(A(k,n)).由定理5,￡R(A(k,n))⊂ ￡R(A(m,n)),所以 P∈￡R(A(m,n)).

推论7 设 n＞m≥0,那么 ø∈￡R(A (m,n)).因而￡ (A (m,n))的最大元∩X∈￡(A(m,n))X=ø.

推论8 ￡R(A (m+1,n)) =￡R(A (m+1)).

定理9 设 n＞m≥0.那么￡R(A (m,n))的特征多项式

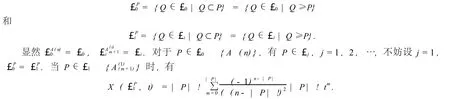
是￡1的秩函数.因为￡0是有最大元 ø和最小元A (n)的有限格,而￡1是有最大元 ø和最小元A(1)m+1的有限格,所以￡0和￡1的特征多项式分别是

[1] 万哲元,霍元极.有限典型子空间轨道生成的格 (第二版)[M].北京：科学出版社,2004：8-54

[2] Huo Y,Wan Z.On the geomertricity of lattices generated by orbits of subspaces under finite classical groups[J].Algebra,2001,243：339-359

[3] Aigener M.Combinatorial Theory[M].Berlin：Spring-Verlag,1979：1-40