转化思想在小学数学“图形与几何”教学中的应用

摘" 要：新课标中对“图形与几何”领域做出了具体的指示，强调要在真实情境中引导学生发现和提出问题，并探索运用正确的数学思想建立模型意识和数学应用意识.本文针对转化思想在小学中高年级“图形与几何”教学中的应用策略进行重点研究，深入探究学生在“图形与几何”实际教学中，数学思维能力的形成过程.

关键词：小学中高年级；数学教学；“图形与几何”；转化思想

小学中高年级数学“图形与几何”教学内容，主要集中在图形的认识与测量以及图形的位置与运动等方面，需要学生从真实的物体中抽象出几何图形，并充分认识图形的特征以及点、线、面的关系，初步形成空间观念.基于此，教师要在教学中着重培养学生的转化思想，引导学生在研究和分析“图形与几何”问题的过程中能够科学合理地进行问题的转化，进一步达到解决问题的目的.

1" 结合教材内容，进行转化思想的具体应用

在小学中高年级“图形与几何”教学中运用转化思想，需要教师紧密地结合教材内容.教材作为数学课程开展的重要依据，其内容中存在着大量可进行转化的内容.因此，教师需围绕教材内容进行具体的转化创设.［1］首先，教师要在备课环节中对教材的内容进行更加清晰、精准地拆解和分析，从而拟定转化思想运用的关键点，实现转化思想的充分利用.其次，教师要结合教材教学内容，拟定转化思想的渗透方式和渗透程度，进而形成对“图形与几何”课程内容的精准把控.

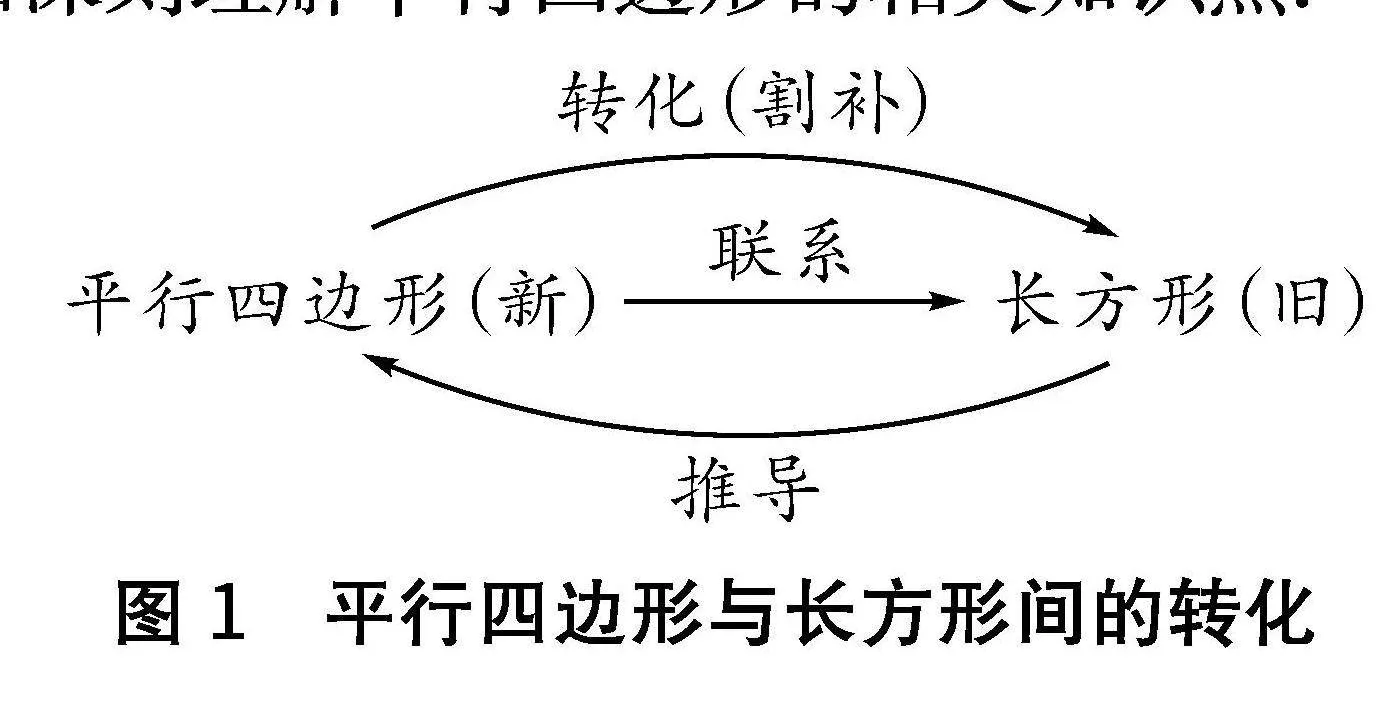
例如，“平行四边形的面积”的主要教学目标是引导学生应用转化思想推导出平行四边形的面积计算公式，从而精准地求解平行四边形的面积，并在观察、操作、分析、归纳等学习过程中，让学生获得良好的数学学习情感.教师要在课程中充分地结合教材内容，进行转化思想的运用.［2］课堂导入环节，教师可以结合问题情境，引发学生的思考.例如，引导学生借助比较大小的方式，辨析平行四边形与长方形的异同点，学生使用基础图形学习方法进行数方格比较大小，但由于平行四边形的图形特征并不太适用于数方格的方法，教师要引导学生借助教材的提示，认真观察平行四边形，并自主寻求新的比较方式.有的学生提出可利用割补或拼接的方式，将平行四边形进行结构重组.教师要鼓励学生大胆地进行动手尝试，积极地开展数学实验，用美工刀和硬纸板等道具，动手验证此种求解的猜想，最终将平行四边形成功地转化为长方形.在动手实践过程中，实现了转化思想的应用（如图1），进而让学生明确清晰认识到平行四边形与长方形的关系，并能够根据长方形的面积计算公式，完成平行四边形面积计算公式的推导.在此过程中，教材内容可起到一定的提示功能，为学生动手实践提供重要的理论支撑，有助于学生更加深刻理解平行四边形的相关知识点.

图1" 平行四边形与长方形间的转化

2" 强化转化思想渗透，进一步达成教学目标

小学中高年级“图形与几何”领域的教学旨在让学生的综合运用能力得到提升，让其能够借助所学知识和方法进行实际问题的解答，显著地提升课程的综合性和实践性.因此，在“图形与几何”课程教学中，教师要充分进行转化思想的渗透，并结合新课标的指导要求，进行具体的教学设计，从而有效地设定和达成教学目标，提升学生的数学学习技能和思维，让其积累有用的数学经验.［3］在具体的数学课堂教学中，教师要科学合理地设定教学目标，并加强转化思想的渗透和应用，结合学生的认知特征及学习需求，构建高效课堂，引导学生感知学习数学的目的.

例如，在“梯形的面积”课程教学中，教师要结合多边形面积单元教学经验，引导学生对未知图形进行转化，实现多个已知图形的拼接，进而有效地对未知图形的面积进行求解.对于梯形面积的求解，可将其转化为三角形，利用三角形面积进行推导，并形成梯形面积计算公式.由此可以设定如下教学目标.

（1）知识与技能目标.掌握梯形面积计算公式及推导过程，并能够精准地进行梯形面积的计算.

（2）过程与方法目标.培养学生观察、操作、讨论、归纳等方面的能力，使其能够掌握数学转化思想，能够科学合理地进行梯形面积的转化推导，初步锻炼学生的空间观念.

（3）情感态度与价值观目标.借助转化探索活动，让学生形成较强的团队合作意识，并能够养成严谨的探究态度，有效地领悟到学习数学的乐趣.

3" 注重转化思想渗透过程，培养学生数学思维能力

转化思想在数学课堂“图形与几何”教学中具有十分重要的地位.教师要注重课堂教学过程中转化思想的渗透，进一步优化课堂教学效果，从而有效培养学生的数学思维能力.

3.1" 导入环节的转化思想渗透

课堂导入环节作为课堂活动的兴趣建立阶段，对学生的学习状态、学习态度、学习互动等具有一定的促进作用.在该环节中进行转化思想的渗透，能够让“图形与几何”课程教学内容更加具象化，便于调动学生对“图形与几何”教学的关注，为后续的新知教学奠定良好的基础，在一定程度上起到降低教学难度的作用.例如，在“不规则物体的体积计算”课程教学中，教师可以借助曹冲称象的故事，对学生的思维形成牵动，让学生能够在不规则物体体积计算过程中，结合转化思想，进行体积的转化求解.

另外，课程导入环节还能够实现旧知与新知的串联，为“图形与几何”课程的新知教学提供支点，便于有效地帮助学生构建数学知识体系，让其能够有效地掌握数学思维与能力.例如，在“三角形的面积”课程教学的导入环节中，教师可渗透转化思想，借助平行四边形面积公式的推导过程，唤醒学生对推导转化方法的认识，进而为三角形面积计算公式的推导提供转化基础.教师可在该课程导入环节中播放平行四边形面积公式推导的微课视频，让学生进行快速的复习，调动学生已有的数学经验和面积计算公式推导记忆，并借助平行四边形面积计算公式推导过程.教师引导学生思考，平行四边形与三角形的关系，并让学生运用割补法和拼接法等方法，借用平行四边形面积计算公式推导过程，进行三角形面积计算公式的推导.

3.2" 新知讲授环节的转化思想渗透

“图形与几何”课程教学过程中，需要教师充分地利用转化思想的渗透，让学生更加深入地对新知识进行解读和思考，强化学生的学习体验.由于“图形与几何”的内容教学探究，更加注重学生逻辑思维和空间想象力的培养.因此，为了让学生能够获得更加流畅的几何知识学习过程，学会思考、学会观察，教师要充分借助转化思想的渗透，开展新知教学，进一步强化学生的认知体验，让其全方位地掌握数学知识.

例如，在“多边形的面积”课程教学中，课程主要针对多边形面积的计算方法进行讲解和阐述.教师需要引导学生熟练地进行多边形的面积计算，并使其能够运用多边形面积计算方法进行实际问题的解决.教师可以借助多媒体课件的动态模拟过程，让学生更清晰地观察多边形，并辨析多边形与已学过图形间的关系，从而拟定使用何种图形面积计算公式进行多边形面积的求解.在具体的图形转化过程中，并不存在着唯一性，教师要引导学生根据已知条件，用多种方法进行多边形面积的求解，进而让其通过多种解题方法的对比，选择最适宜的求解方式，良好地运用数学转化思想进行解题.

3.3" 练习应用环节的转化思想渗透

为保证数学课堂的完整性，教师还要将转化思想渗透于课堂的练习应用环节，让学生能够更深入地进行转化思想的学习和应用，掌握正确地解决“图形与几何”问题的方法.数学课堂练习应用环节的教学目的主要是帮助学生加深对所学知识的认识，并使其能够巩固数学解题方法的应用，起到夯实课程知识的效果.在此环节中进行转化思想的渗透运用，对学生数学思维的形成有着极大的帮助.因此，该环节除了要进行课堂重难点的针对性练习，还要对学生的转化思想进行有效训练.在具体练习应用环节设计中，教师设置的问题类型要多样化，对学生的转化思想进行针对性的训练和强化，进一步帮助学生积累解题经验.例如，在“三角形内角和”的课堂练习应用环节，教师可以针对内角和的概念及应用，进行转化思想的训练，借助正六边形内角和的计算练习，让学生进行三角形内角和的转化训练，运用拆分法对正六边形进行转化，让学生的数学模型思维和空间观念得到进一步的锻炼.

3.4" 复习总结环节的转化思想渗透

数学课堂中的复习总结环节，是进一步巩固转化思想应用的关键环节.该环节能够让学生的逻辑思维得到系统化的梳理，并让学生更加清晰、有效地认识到“图形与几何”教学领域中，转化思想的重要性，有助于学生数学思维的提升.例如，在“圆的面积”课程复习总结环节中，教师可以先引导学生对本节课的教学内容进行总结.有的学生说他学会了圆的面积计算公式；有的学生说他认识到圆与平行四边形存在着极大的相似性和联系，可以借助平行四边形面积计算公式进行圆的面积计算.教师要着重针对圆的面积公式推导过程中运用的转化思想进行总结，让学生加深对转化思想的认识和应用.

4" 优化课堂教学方式，提升学生的转化思想感悟

《义务教育数学课程标准（2022年版）》强调要针对不同学段学生特点，采用适宜的教学方式，从而引导学生综合地运用数学学科知识与方法解决问题.相比以往的数学课程教学，此种教学改变更能够让课堂实现精准教学，并关注学生主体的学习需求，让其形成知识及技能的培养.尤其针对小学中高年级的“图形与几何”教学，更需要学生掌握解题的过程，增强解题的灵活性，提升学生的数学知识应用能力.基于此，教师要尝试在课堂教学中，着重提升学生对转化思想的感悟，并引导学生积极地进行实践操作，验证转化思想的正确性，进一步深化学生对转化思想的理解，有效地降低“图形与几何”课程教学难度.

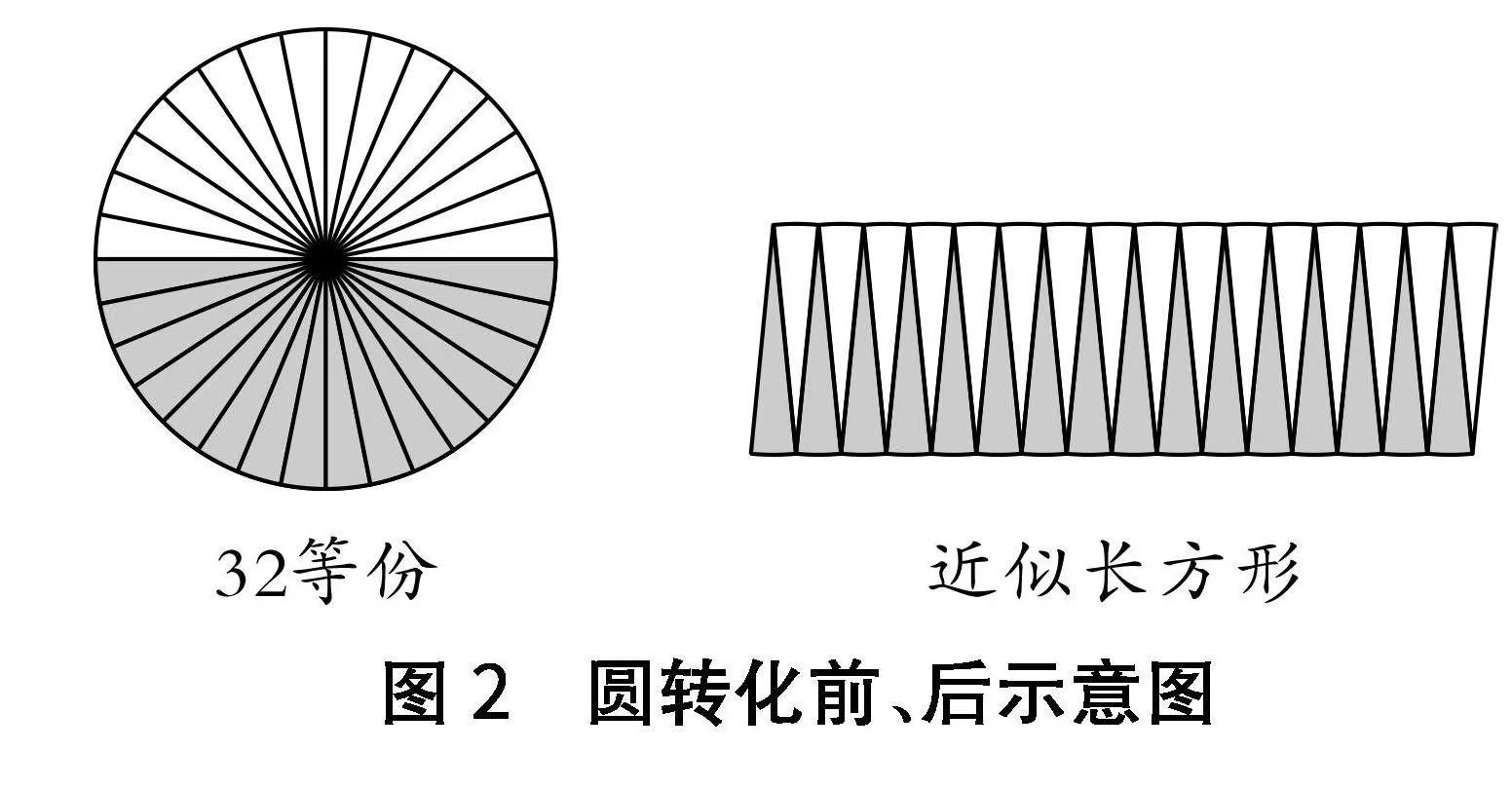
例如，在“圆的面积”教学过程中，由于学生已经初步具备了几何图形的相关学习经验，能够知晓转化思想在图形面积求解过程中的重要作用，教师要在教学中积极地鼓励学生进行大胆想象，并动手实践操作进行转化思想的验证，进而推导出圆的面积计算公式.课堂中，教师可先利用多媒体课件进行圆的面积推导演示，然后引导学生进行动手操作，将提前准备好的圆形纸片进行裁剪，分别分成16等份、32等份、64等份，并利用图形碎片进行相应图形的拼摆，最终可发现平均裁剪的份数越多，结果计算越精确.如图2所示，最终可将圆形纸片拼接成为近似长方形的图形，此时近似长方形的底边长为圆周长的一半，宽与圆形半径相等，最终可根据长方形的面积公式完成圆的面积公式推导.该推导过程中涉及转化思想和极限思想，即可尽量将圆形的裁剪次数极限延伸，用以降低转化中的误差.通过动手操作对转化思想的验证，能够一定程度上提升学生对转化思想的感悟，使其能够更有效地借助转化思想进行数学问题的解答.

图2" 圆转化前、后示意图

5" 结语

转化思想是小学中高年级数学“图形与几何”教学中的重要数学思想方法，其能够将抽象的知识点具象化，并让学生的逻辑思维能力得到显著提升，对构建高效课堂具有重要的帮助.在实际应用中，教师要充分关注转化思想的渗透程度，并关注各课堂教学环节中转化思想的应用形式，让学生能够高效地进行“图形与几何”方面的知识学习，为学生的数学高阶思维形成奠定基础.

参考文献

［1］蔡益磊.转化思想在小学数学“图形与几何”教学中的实践［J］.理科爱好者，2024（1）：235-237.

［2］苏邦屯.浅谈转化思想在小学数学图形与几何中的应用［J］.学苑教育，2023（24）：82-83＋86.

［3］孟元春.立足学生思维发展，渗透数学思想方法——转化思想在小学数学“图形与几何”中的应用［J］.数学学习与研究，2022（36）：68-70.