借助数学活动 发展抽象能力

《义务教育数学课程标准（2022年版）》指出数学课程要培养的学生核心素养主要表现为：抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。基于此，教学设计及实施如何指向核心素养的培养，让学生的抽象能力得到应有的发展呢？笔者认为，学生在课堂中参与的各种教学活动是培养核心素养的重要载体，教师可以以启迪学生思维、发展学生数学能力的数学活动为抓手，设置有价值的问题，引导学生积极动手、动口、动脑，在操作活动中，让学生的思维从直观感知上升到抽象归纳，从而达成教学目标。下面，笔者以苏科版数学七（上）“图形的运动”的教学为例，具体谈谈数学活动的设计与实施。

一、教学目标

借助生活实例，抽象出图形的运动变化，感悟“点动成线，线动成面，面动成体”；通过仔细观察、动手操作等活动，认识图形的平移、旋转、翻折等三种变换方式，感悟让图形“动”起来是研究图形性质的重要方法；经历“观察→思考→探究→实践→思考”等过程，感受数学与生活的联系，体会转化、分类等数学思想，培养观察、分析问题的能力，提升抽象能力、几何直观等核心素养。

二、教学过程

1.课堂引入

教师播放动画《生活中的运动现象》。动画中有雨点从空中落下、汽车雨刮器运动、宾馆的旋转门在旋转等画面。

师：你还能举出生活中类似的运动例子吗？

随后，教师引导学生用数学的眼光将生活中物体的运动抽象成图形的运动。

【设计意图】通过动画，学生感受生活与数学的密切联系，学着用数学的眼光观察世界，即学着由生活中的运动抽象出图形的运动。

2.动手操作，探究体验

活动1：探究点、线的运动。

问题1：把笔尖看成点，这个点在纸上运动时形成了什么图形？你还能举出生活中这样的例子吗？

问题2：把笔抽象地看成一条线，这条线可做什么样的运动？可以形成什么样的图形？你还能举出生活中这样的例子吗？

用多媒体分别进行动态展示，请学生用语言分别概括从这些运动中观察到的数学现象。

【设计意图】学生的学习应该是现实的、有意义的、富有挑战的。学生在已有的认知水平和知识经验基础之上，发现点的运动可以形成线，线的运动可以形成面，多媒体的动态展示使学生深刻感悟“点动成线”“线动成面”。通过举例、动画展示、自制学具，学生能更加直观地感受知识的生长过程，激发探究欲望。

活动2：探究面的运动。

请学生利用事先准备好的长方形纸片、直角三角形纸片、圆形纸片，进行动手操作，探究它们可做什么样的运动，可以形成什么样的图形。学生先独立思考，再分组合作、交流展示。随后，教师用几何画板展示，请学生用语言概括从这些运动中观察到的数学现象。最后，师生一起回顾几何画板动画，总结构成图形的最基本元素。

【设计意图】给学生留足独立思考的时间和交流机会，让学生类比线的运动，动手探究面的运动，了解知识的发展过程，真正成为课堂的参与者，既获得数学知识，积累活动经验，又发展探究精神和创新意识；运用几何画板进行演示、回顾，学生的思维从直观感知上升到抽象归纳，总结得出“点是构成图形的最基本元素”。

活动3：拼一拼。

问题3：将两块相同的直角三角尺相等的边拼在一起，可以拼成哪些不同的平面图形？请你说出这些图形的名称。

【设计意图】以自主、合作、探究的方式组织学生学习，让学生体会复杂的图形是由简单图形运动组合而成的，渗透分类讨论的数学思想，培养学生的观察能力、问题分析能力及合作意识。

活动4：试一试。

问题4：对于活动3中拼出的每一个图形，请你让其中一块三角板不动，操作另一块三角板，通过哪种方式运动后，它能与不动的那块三角板完全重合？

【设计意图】学生通过让图形“动”起来，不断探索图形与图形之间的变化，感悟“让图形动起来”是研究图形性质的重要方法，进一步认识和体会图形的平移、翻折、旋转；经历自主尝试、动手操作，学着从复杂图形中甄别能够完全重合的三角形，即全等三角形，为后续学习相关知识做铺垫。过程中还可以让学生用语言描述图形的运动，引导学生清晰正确地表达，一方面帮助学生加深对概念的理解，另一方面培养学生的数学语言表达能力。

活动5：画一画。

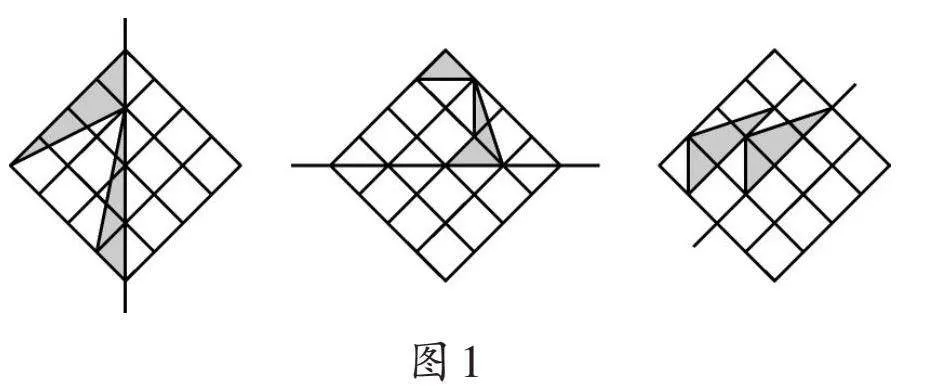
问题5：如图1，在空白方格中画出相应的图形，使直线一旁的阴影图形沿直线翻折后能与直线另一旁的图形完全重合。

问题6：图2是由“ ”向右平移而成，把图2沿虚线剪开，虚线以下的部分向右平移4格，能得到什么样的图形？请在图3中画出来。

问题7：如图4，如何操作，图中的三角尺才能旋转到虚线所示的位置？

【设计意图】三个问题分别涉及图形的翻折（对称）、平移、旋转，同时还渗透从一般到特殊的数学思想。通过画图，学生感悟到图形的变换其实是“点”的变换，能画出变换后的“对应点”是解决问题的关键。

活动6：剪一剪。

问题8：如何用剪刀剪出如图5所示的“红双喜”呢？

问题9：请在生活中举出“翻折、平移、旋转”的应用实例，并与同学进行交流。

【设计意图】设计剪纸活动，学以致用，引导学生进一步体会图形“翻折”运动在现实生活中的运用，领略数学之美，积累活动经验并发展空间想象、几何直观等能力。

3.总结反思

师：请同学们回顾一下，经历了这节课的学习，你有哪些收获与感想？

【设计意图】学生对所学的知识及时巩固，使其条理化、清晰化，形成自我反馈，从而构建起自己的知识经验，形成自己的见解。

4.作业布置、板书设计（略）

三、教学反思

本节课以数学实验活动为载体，设置了“点动、线动、面动”问题，让学生经历观察、操作、探究、思考等过程，总结出“点动成线、线动成面、面动成体”；借助多媒体的动态演示，引导学生直观感受知识的发生与发展过程，让学生的思维从直观感知上升到抽象归纳，从感性认知转变到理性思考。在学生的动手操作过程中，笔者设计了拼一拼、画一画、剪一剪等活动，帮助学生体会并认识了平移、旋转、翻折运动方式，强化了学生的直观体验，让学生深切体会到图形运动的实质就是点的运动，复杂的图形常常由简单图形运动变换组合而成，感悟到研究图形性质的重要方法是让图形“动”起来，引导学生在变中寻求不变的本质，感悟转化、分类等数学思想方法，为学生后续的学习奠定了良好基础。在这个过程中，学生逐渐学会用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界，逐步发展核心素养，培养数学品质。

（作者单位：江苏省宿迁市宿城区新区初级中学）