基于核心素养的初中数学课堂教学策略分析

邬建霞

【摘要】文章以建构高效数学课堂为出发点，以促进初中生数学核心素养有机形成与自然生长为目的，依托《义务教育数学课程标准（2022年版）》对在初中数学课堂中应培养的学科核心素养作出了简要分析，并在此基础上，结合苏科版八年级上册数学教材“一次函数、一元一次方程和一元一次不等式”一课内容，从课前、课中及课末三个维度上对在数学课堂中稳定培育学生数学核心素养的策略方法进行了例谈与思考，旨在增强初中数学课堂教学的“素养本位”倾向，推动“立德树人”根本任务落地.

【关键词】核心素养；初中数学；教学策略

《义务教育数学课程标准（2022年版）》（以下简称《数学课标》）指出，核心素养导向的教学目标是对“四基”“四能”教学目标的继承和发展.“四基”“四能”是发展学生核心素养的有效载体，核心素养对“四基”“四能”教学目标提出了更高要求.义务教育阶段的数学课程，应确立以核心素养为导向的课程目标，设计能体现出数学课程结构化特征的课程内容，实施促进学生发展的教学活动，以持续丰富学生的数学“四基”，发展学生的数学“四能”，让学生通过数学的学习，养成良好的数学学习习惯，形成积极的情感态度价值观与数学核心素养.基于这一认识，文章便专注于初中数学课堂教学，从简析初中生所需形成的数学核心素养入手，对在具体的数学课堂教学中培养学生核心素养的策略方法进行案例分析.

一、初中生数学核心素养简析

《数学课标》在“课程目标”中以“三会”：会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界，简要概括了义务教育数学课程应培养的学科核心素养，且在“课程理念”中明确指出，不同学段学生所需形成与发展的数学核心素养水平各不相同.因此，为在新课标视域下的初中数学课堂教学中，实现对学生数学核心素养的针对性培养，身为学习组织者、引导者及合作者的教师就要以《数学课标》为依据，对初中阶段的数学核心素养内涵作出深入分析.

《数学课标》在“核心素养内涵”部分中明确指出，初中阶段的数学核心素养侧重对概念的理解，主要表现在抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识和创新意识九个方面上.其中，抽象能力、几何直观、空间观念与创新意识属于数学眼光维度；运算能力、推理能力属于数学思维维度；数据观念、模型观念和应用意识则属于数学语言维度.

在初中数学课堂教学中培养学生的数学“三会”，在某种意义上就是培养与锻炼学生发现、提出、分析、思考与解决处理问题的数学学习能力.由此，教师就可遵循学生的认知水平发展规律，通过创设衔接现实的问题情境、布置诱导合作探究的驱动任务与组织指向迁移运用的综合实践等方式，将培养学生数学核心素养的育人工作与数学课堂中的教学活动密切联系起来，以此不断加强初中数学教学的核心素养导向，促进高效数学课堂的形成.

二、基于核心素养的初中数学课堂教学———以“三个一次”为例

“一次函数、一元一次方程和一元一次不等式”是苏科版八年级上册数学教材第六章“一次函数”的第六课时.在本课中，学会用函数的观点看方程与不等式，是八年级学生所需掌握与熟练应用的基本数学思想方法，这不仅直接影响着初中生对函数、方程与不等式意义及联系的理解认识，还对初中生后续学习高中数学中的“三个二次”关系起着举足轻重的作用.基于此，文章便以本课为进行案例分析的主要对象，对在初中数学课堂中培养学生数学核心素养的有效做法展开思考.

（一）课前：衔接现实创设问题情境，在发现问题、提出问题中发展数学眼光

基于对初中生数学眼光内涵的分析可知，立足真实情境，主动从数学学科的角度发现并提出有意义的数学问题，是学生形成抽象能力、几何直观、空间观念和创新意识的集中表现.由此，教师在“一次函数、一元一次方程和一元一次不等式”一课的课堂教学中，实施与展开培养学生数学眼光的核心素养育人工作时，就可为学生创设与现实世界、日常生活有紧密关联的真实问题情境，在优化与革新传统数学课堂中课程导入形式的同时，更好地激发学生探索未知的好奇心和求知欲.

苏科版八年级上册数学教材在本课中设置了“求弹簧在所允许的限度内所挂物体的最大质量”的数学例题，意在让八年级学生通过分析思考该例题，感知与体会到一次函数与一元一次方程、一元一次不等式之间所存在的紧密联系，掌握并理解用函数的观点看方程与不等式的数学思想方法.

在应用情境教学法为学生创设衔接现实的真实问题情境时，教师可从数理融合的角度入手，关联学生的实际生活，在课堂中为学生演示测量25cm弹簧在允许限度内所挂物体最大质量的物理实验过程：首先，将一根长为25cm，长度限度不超过35cm的弹簧顶端固定在铁架台上，另一端悬挂砝码；然后，准备若干个重为1kg的砝码，依次叠加地悬挂在弹簧的另一端上，测量每悬挂1个1kg砝码时，弹簧的伸长长度；最后，统计物理实验数据（表1）.如此，学生的注意力与眼光便会被教师的动手操作所吸引，课堂参与度自然也会得到相应的提升.

而在演示实验结束后，教师则可立足物理实验数据，向学生提出具有一定启发性的问题：“在允许的限度内，这根弹簧最多可悬挂质量为多少的砝码？弹簧所悬挂物体质量与其伸长长度之间存在怎样的关系？在允许限度内，这根弹簧能悬挂的物体质量范围在什么区间内？”将学生的注意力合理转移到对实验数据的分析上，促使学生主动地从数学的角度，将弹簧所悬挂的物体质量设为xkg，弹簧长度设为ycm，根据实验数据，列出关于x与y两个变量的一次函数表达式，即y=0.5x+25，且应用描点法动手绘制出这个一次函数的图像（图1）.

一部分学生会从函数的角度分析教师所提出的问题，即通过观察一次函数y=0.5x+25的图像可知，当y=35时，x=20；当y=25时，x=0.所以，该弹簧所挂物体质量最大是20kg，在允许限度内，该弹簧可悬挂物体的质量在0～20kg内，有0≤x≤20.另一部分学生会从方程的角度对解决问题的方法提出不同见解，即根据物理实验数据可知，弹簧所挂物体质量越大，弹簧长度越长.因为弹簧伸长的最大允许范围是35cm，弹簧原本长度是25cm，所以可得到两个一元一次方程，0.5x+25=35（1）；0.5x+25=25（2），解方程可得，x1=20，x2=0.所以，该弹簧所挂物体质量最大是20kg，在允许限度内，该弹簧可悬挂物体的质量在0～20kg内.还有一部分学生能够从一元一次不等式的角度上，处理分析物理实验结论，即已知弹簧原本长度为25cm，最大伸长长度为35cm，则有一元一次不等式25≤0.5x+25≤35，解一元一次不等式可得，0≤x≤20.所以，该弹簧所挂物体质量最大是20kg，在允许限度内，该弹簧可悬挂物体的质量在0～20kg内.

在这一过程中，学生不但亲身经历了知识迁移过程与类比推理过程，而且在从数学的角度分析处理物理实验情境中的实验结论问题时，也会因观点不一致而实现思维碰撞，进而主动发现并提出“为什么分别从函数、方程与不等式的角度分析问题，均能得到相同的答案？一次函数与一元一次方程、一元一次不等式之间是否存在一定的联系？”等数学问题，求知欲与探索欲自然也会在潜移默化中有机形成.

（二）课中：合作探究铺设驱动任务，在分析思考问题中发展数学思维

探究与实践，既是《数学课标》倡导与鼓励的数学学习方式，也是在初中数学课堂教学中锻炼学生数学思维能力、问题解决能力、独立思考能力和合作学习能力的有效路径.由此，教师在核心素养导向下，围绕“一次函数、一元一次方程和一元一次不等式”一课展开课中教学活动与教学实践时，就可充分借助任务驱动法，为学生精心设置与铺设更具探究性、实践性与综合性的驱动型数学学习任务，以此为深入探索与发现“三个一次”关系搭建可依赖的稳定数学学习支架，让学生在积极分析与合作探讨数学问题的过程中，实现思维能力进阶，提升数学问题思考能力与数学学习能力.

在学生出于总结归纳物理实验结论的目的，认真分析思考课程导入环节中物理实验数据，对一元一次函数、一元一次方程与一元一次不等式的关系生成好奇心与求知欲后，教师可依据学生的数学学习能力、思维能力与问题解决能力，遵循科学的小组划分原则，组建数学学习小组，并向各个数学学习小组布置与提出如下极具探究价值的驱动型数学学习任务，驱动学生以小组合作的学习形式展开数学探究与数学实践.

【驱动型数学学习任务一】下面三个一元一次方程有哪些共同点和不同点？请从一次函数的角度对解这三个一元一次方程的过程作出合理解释.

（1）2x+1=3；（2）2x+1=0；（3）2x+1=-1.

【驱动型数学学习任务二】下面三个一元一次不等式有哪些共同点和不同点？类比用一次函数解一元一次方程过程的方式方法，从函数的角度解释说明解一元一次不等式的过程.

（1）3x+2>2；（2）3x+2<2；（3）3x+2<-1.

【驱动型数学学习任务三】一次函数、一元一次方程和一元一次不等式之间有极为紧密的关系，请根据一次函数y=2x+6的图像（图2），说出一元一次方程2x+6=0和一元一次不等式2x+6<0，2x+6>0的解.

【驱动型数学学习任务四】一次函数与方程组、不等式组之间是否也存在类似“三个一次”的关系？请从函数的角度，分析并解决下列二元一次方程组的问题.

【问题】表2为两种移动电话的计费方式，用函数的方法分析两种计费方式费用相等的情况.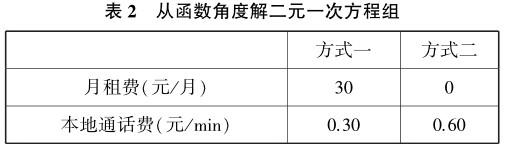

如此，学生便会通过合作分析与探索探究以上四项驱动型数学学习任务，深刻体会与感受到一次函数与一元一次方程、一元一次不等式及二元一次方程组之间的紧密联系，即任何以x为未知数的一元一次方程、一元一次不等式都可改写为ax+b=（或>或<）0（a≠0）的形式.所以，解一元一次方程相当于求某个一次函数y=ax+b，当y=0时，自变量x的值；解一元一次不等式相当于求某个一次函数y=ax+b，当y>0或y<0时，自变量x的值.二元一次方程组是由两个二元一次方程联合而成的方程组，其中每个二元一次方程都可改写为y=kx+b的形式，所以二元一次方程也对应一个一次函数.从“数”的角度来看，解二元一次方程组相当于求两个函数值相等时自变量的值；从“形”的角度来看，解二元一次方程组相当于看两个一次函数对应直线相交时的交点坐标.除此之外，初中生的数学运算能力、推理能力也会在合作开展多种解方程、解不等式、解方程组、画函数图像与分析函数、方程、不等式及方程组间的联系的过程中，得到相应的锻炼与强化.

（三）课末：迁移运用组织综合实践，在解决处理问题中发展数学语言

学以致用、迁移创新是初中生在数学课程学习中实现深度学习的主要表现，同样这也是学生形成与发展数学语言的突出特征.函数、方程、不等式与方程组是从现实世界中相等或不等数量关系中抽象而来的数学模型与解题工具，与初中生的日常生活有着极为密切的联系.在学科核心素养视域下的初中数学课堂教学中，教师可在学生通过合作探究，深刻理解并认识“三个一次”关系后，在课末环节中为学生布置指向简单实际问题解决的数学应用问题，启发学生迁移运用方程与不等式、数形结合等数学思想方法解决问题，以此加深学生的数学学习感悟，升华学生的数学学习体验.

【习题一】拼多多与淘宝是现实生活中人们常用的两大网购平台.在“双十一”期间，两家网购平台开展了不同的优惠活动.拼多多所有商品按8折出售，淘宝对一次购物中超过200元的价格部分打7折.那么，在“双十一”期间，如何选择网购平台？

结 语

总而言之，在新课标视域下的初中数学课堂教学中，教师可在依据《数学课标》充分掌握初中生所需形成的数学核心素养的基础上，立足课堂教学实际，将培养学生数学核心素养的育人工作与课堂中的关键教学环节及教学活动融合起来，在持续增强与提升初中数学课堂的教学有效性与育人实效性的同时，更好地引领初中生数学学习方式的变革与转化，推动学生数学核心素养的形成.

【参考文献】

[1]巫锦娟.基于数学核心素养理念的初中数学课堂教学策略[J].数学大世界（下旬），2021（11）：49-51.

[2]崔向婕.核心素养下初中数学课堂有效教学策略的研究[J].读写算，2021（32）：151-152.

[3]何江.基于核心素养下的初中数学课堂教学策略：以数学建模为例[J].数学学习与研究，2021（30）：34-35.

[4]李秀.试论数学学科核心素养下基于自然生长的初中数学课堂教学策略[J].数学学习与研究，2021（19）：104-105.