初中数学常见错题归类及解题技巧研究

贾龙才

【摘要】学生在解决数学问题时出现的错误往往暴露出其学习能力不足.整理学生的错题，并对错题原因进行分析、归类，有利于教师进一步掌握学生的学习动态，从而提高教学针对性，提升学生综合能力.文章立足于教学实践，对代数、几何、统计等类型的数学错题进行整理，将其分类为知识型错题、思维型错题、态度型错题，并给出具体案例.同时，文章剖析三类错题成因，以期为进一步提高初中数学解题教学质量提供参考.

【关键词】初中数学；错题；归类；教学技巧

引 言

数学学习的过程本身就是不断犯错、改错的过程.合理归类错误并辨明其原因，落实配套的改错教学，可促进学生与教学内容的有效交互，使其在练习、纠错、反思的过程中形成深刻认知.实际教学中，教师有必要认识到错题教学的重要性，先对常见错题进行归类，之后结合典型错误案例说明错误原因，指导学生反思自身的解题情况，使其在观察案例的过程中反思自身，做到“有则改之，无则加勉”.

一、初中数学常见错题归类

初中数学常见题目类型有很多，如实数、整式、函数的计算，线段垂直、平行的判断，三角形相似或全等的证明，概率计算，等等.围绕数学知识点对错题进行归类，可将初中数学错题分为数十类，极大地增加了错题教学的复杂性.而从错因角度出发对错题进行归类，则使错题体系变得简单得多.观察学生的解题过程，发现造成其解题错误的原因不外乎以下几个：知识遗忘或混淆导致解题错误，主观判断或惯性思维造成解题错误，审题时漏掉或错看关键信息造成解题错误，解题计算时不认真导致结果错误，等等.根据解题错因，可大致将初中数学错题归类为知识型错题、思维型错题、态度型错题三类.

（一）知识型错题

1.代数知识掌握不扎实导致错题

代数知识以数的概念、算理、算法为主，包括实数的分类，单项式、多项式的概念及合并同类项的方法，一元一次方程、一元二次方程、二元一次方程（组）的概念及解法，等等.笔者在初中数学教学中发现，学生存在代数理论知识掌握不扎实的情况，导致其在解题时出现错误.以人教版七年级数学上册“有理数”的单元练习教学为例，有知识型错题如下：

2.几何知识掌握不扎实导致错题

初中数学几何内容由图形的性质（点、线、面、角、相交线、平行线等）、图形的变化（轴对称、旋转、平移、相似、投影等）、图形与坐标（平面直角坐标系、图形的运动与坐标等）三部分构成.各部分知识互有关联，学生在学习过程中，容易因理解不到位而出现知识遗忘、混淆等问题.以人教版七年级数学下册“相交线与平行线”的单元练习教学为例，有知识型错题如下：

错解 B选项或C选项.

解析 此题以平行线的性质为主要考点，包括：①两直线平行，内错角相等；②两直线平行，同旁内角互补；③若一个角的终边与始边互为反向延长线，则这个角叫作平角，若两个角的和等于180°，则称这两个角互为补角.分析错题原因，发现选择B选项的学生将平行线的性质错记为“两直线平行，内错角互补”，之后构造平行线得出∠3=250°；发现选择C选项的学生混淆平行线性质，按照“两直线平行，内错角互余”，构造平行线得出∠3=70°.按照正确的知识点，应作平行线c平行于直线a，将∠3分为∠1与∠2的内错角，之后按照“两直线平行，内错角相等”的性质计算，得出正确的是A选项.

（二）思维型错题

1.思维定式类型错题

思维定式是指在定向思维的影响下出现的思维趋向性、专注性状态.思维定式在初中数学教学中是客观存在的，具有正、反两方面的作用.正向作用在于思维定式可帮助学生快速回顾已掌握的数学知识、原理、思想方法，从而迁移新知，解决类似问题.负面作用在于思维定式会限制学生的学习视野，使其局限于自身的知识体系，不能灵活变化角度分析并解答新问题.在初中数学解题过程中，常有学生因思维定式生搬硬套数学定理、公式来解决问题，导致答错.以人教版八年级数学上册“全等三角形”的单元解题教学为例，有思维定式类型错题如下：

例3 如图2所示，点O表示港口，A，B分别表示的灯塔与港口距离相等.OA，OB表示海岸线，一艘货轮从港口驶出，计划沿∠AOB的平分线航行.航行过程中，有人测得货轮距A，B两个灯塔的距离相等，试着判断货轮是否偏离指定航线.

错解 根据相关知识，到角两边距离相等的点在角平分线上，但题中给出的是到A，B的距离，所以无法判断.

解析 这一问题以角的平分线为主要考点，学生在解题时也考虑到应用此知识解答问题，但是，受思维定式的影响，直接将“角的内部到角的两边的距离相等的点在角的平分线上”生搬硬套到解题过程中，并未想到角的平分线将一个角分成了两个度数相等的角这一实质.解答这一问题，可从全等三角形的角度出发.如图3所示.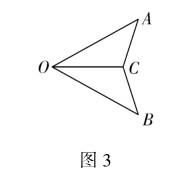

结合题目给出的信息，可以发现OA=OB，AC=BC，OC=OC，由此判断△AOC≌△BOC，得到∠AOC=∠BOC，即OC平分∠AOB，所以该货轮并未偏离指定航线.

2.主观判断类型错题

思维是对经验的改组，是探索、发现新事物的心理过程，具有概括、间接认识客观事物的功能.解决数学问题需要学生从客观的角度分析问题的表象，挖掘其本质，并基于已掌握的数学概念、定理、思想方法找准解题切入点，按照确切的逻辑进行.但是，有的学生在解题时存在主观思维过强的问题，具体表现为：主观臆断题目考查内容，想当然地为题目添加新的解题条件，等等.其原因在于学生主观意识过于强烈，不能从客观角度出发分析并解决数学问题.以人教版八年级数学下册“勾股定理”的单元习题教学为例，有主观判断类型错题如下：

（三）态度型错题

1.审题不细致

审题是解题的第一步，学生只有认真审题，明确题目要求的是什么、给出了怎样的关键信息、不同数量间的关系是什么，才有可能找对解题切入点，顺利解题.但是，目前仍有学生在审题时不认真，导致解题出现纰漏.比如，一些学生过于自信，审题后未对题目给出的条件、信息进行深入思索，对照以往所解答的数学问题直接照搬解题套路；再如，一些学生急于求成，粗略读题，忽略题目给出的关键信息、题目中的隐藏信息，导致解题失败等.以人教版九年级数学下册“相似”的单元习题教学为例，有审题不细致的错题如下：

解析 这一问题以比例为考点，是一道非常简单的习题，只需结合题目给出的信息计算比例即可.上述错解中，学生在审题时不认真，漏看了两条线段长度单位的差异，即线段AB的长度单位是毫米，线段CD的长度单位是厘米，在计算二者的比例时，应将二者转换为相同的长度单位再求解.正解为：因为AB=2mm，CD=6cm=60mm，所以AB∶CD=2∶60=1∶30.

2.计算不认真

计算是得到问题正确答案的手段.学生只要准确掌握算理算法，即可解决基本的数学运算问题.但是，在实际教学中，有的学生常出现代错数值、忽略变号等问题，导致计算结果错误.原因是计算态度不认真，未能在计算时将正确数值代入算式，或未能在计算后采取正确检验方法检验结果.以人教版九年级数学上册“二次函数”的单元习题教学为例，有计算型错题如下：

例6 如图4所示，在平面直角坐标系中，点A，C的坐标分别为（-1，0），（0，-3），点B在x轴上.已知某二次函数的图像经过A，B，C三点，且它的对称轴为直线x=1.求该二次函数的解析式.

二、教学反思

学生解题错误，其原因不外乎基础不牢固、思维僵化、解题态度不严谨等.明确错因，并对症下药，可在一定程度上避免学生犯错.教师应专注课程教学，及时发现学生的问题并为其进行点拨、解惑，从根本上促成其对数学概念、性质等理论知识，数学思想方法等程序性知识的内化吸收，确保其能够从不同角度出发灵活解决疑难问题.

结 语

错题是一类不可忽视的重要教学资源，围绕其展开初中数学教学工作，可使教师更加深刻地认识到学生对数学基础知识的掌握情况、数学思维及解题能力的发展情况.教师应当明确数学错题的育人价值，并关注学生在代数、几何、统计学知识中的错误情况.收集错题并对其进行分类整理，以便明确学生的错误原因，从而采取加强基础知识教学、思维训练等针对性教学策略，为提高初中学生的数学综合能力提供支持.

【参考文献】

[1]游冬妮.初中数学典型易错题分析及应对策略[J].中学教学参考，2022（35）：25-27.

[2]战文颜.初中数学解题策略的研究及应用[J].数理天地（初中版），2022（23）：69-71.

[3]高雁.有效教学理论下的初中数学复习课教学[J].数理天地（初中版），2022（23）：78-80.

[4]司淑萍.新时期初中数学解题策略与数学思维的研究[J].数学学习与研究，2022（31）：38-40.