依托精准“追问”?助推思维发展

曾佳

【摘 要】追问是数学课堂中常用的教学手段，精准的追问有助于学生更透彻的理解学习内容，发展数学思维。文章以“解决问题的策略（画图）”一课为例，通过课上的五次“追问”，帮助学生理解方法、感受共性、把握本质、体会价值、发展思维。

【关键词】追问 核心素养 数学思维

追问，顾名思义就是多次的问、刨根究底的问。数学上的追问，指的是教师在教授某一教学内容时，为了能让学生理解的更加透彻，提问之后再次提问。追问是教师对课堂内容的“二次开发”，有效的追问能让学生对知识的把握由浅入深、由模糊到清楚、从单一到丰富。教师在教学中精准的追问，有助于学生思维的发展和核心素养的养成。

“解决问题的策略（画图）”是苏教版数学四年级下册的一节课，学生在学习这节课时，需要经历画线段图、分析线段图解决问题的过程，从中感受画图的策略的优点和价值。那么，如何能让学生在学习过程中对画图策略的本质理解的更加透彻？在教学时，笔者特别注意五处“追问”，助推学生思维的发展。

一、课上追问，助推学生思维发展

（一）游戏中“追问”，孕伏方法

一节课中导入环节的目的，是让学生能更好的进入新课的学习。本节课中，笔者设计了一个热身小游戏，在游戏中“追问”，为学习解决问题的策略做好孕伏。

片段1：游戏处追问

谈话：小宁和小春喜欢收集邮票，我们用圆片表示他们收集的邮票的个数，怎样做能让他们的邮票同样多呢？

学生回答3种解决方法：（1）给小春添上2枚；（2）给小宁去掉2枚；（3）把小宁多的2枚中的1枚给小春。

基于以上的热身活动，教师提出第一个追问：

[追问1]为什么不能把多的2枚都给小春呢？

学生回答的三种方法中，前两种方法，无论是给小春添上两枚，还是给小宁去掉两枚，都是在其中一个人的邮票数不变的情况下，改变另外一个人的邮票数，使两人的邮票数变得相等的。第三种方法更难理解，需要将多出来的两枚中的一半分给小春。在后面通过线段图解决问题的过程中，也是学生容易出错的点。笔者在游戏中提出追问，有助于学生在后面策略的学习中发散思维，更加精准的寻找更多解决问题的方法。

（二）探究中“追问”，感知共性

新知教学环节是教学的“关键处”。“关键处”适时的追问是对学生思维“再开发”的过程。知识的学习是从浅到深，层层递进的过程，往往需要通过一次次对关键问题的研究，才能体会到一类问题的共性所在，同时得到思维上的发展。

片段2：“关键处”追问

1.出示例题：小宁和小春共有72枚邮票，小春比小宁多12枚。两人各有邮票多少枚？

提问：现在两人邮票数之间的关系是怎样的？如果要画图表示，现在还可以用圆片吗？为什么？

生：不知道小宁和小春邮票的具体数量，不能用圆片来表示。

提问：那么可以怎样表示小宁和小春的邮票数呢？

2.尝试画图：现在我们用两条线段表示出了两人的邮票数，你能在线段图上将题中的条件和问题表示出来吗？

3.列式解答：看着线段图分析，并尝试列式解答，并在小组中说一说每一步算的是什么。

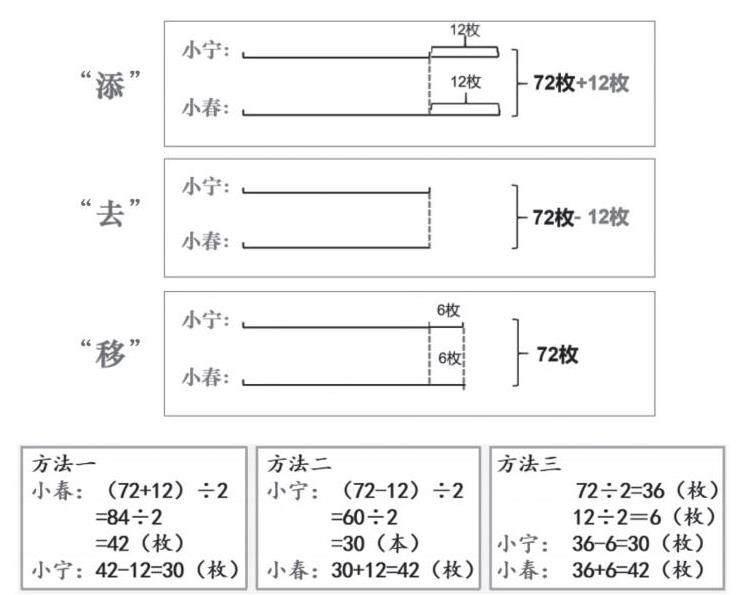
4.展示方法：

至此，借助线段图，解决问题的三种方法“添”“去”“移”，已经全部呈现给学生，课堂已经到了“关键处”，那么这三种方法的共性在哪儿呢？教师在此处提出了第二个追问：

[追问2]不管是给小宁添上12枚、给小春去掉12枚、将小春多的12枚分一半给小宁，目的都是什么？在变化的过程中，有什么不同之处？

通过追问总结共性，虽然这三种方法思考问题的角度不同，但本质是一致的：都是设法让两人邮票的枚数变得同样多，使两个原本不相等的数量转化成相等的数量。要特别注意的是，前两种方法在使两人邮票枚数变得同样多的过程中，邮票总枚数也会发生相应的变化，第三种方法总数不变。

学生思维的发展是循序渐进的过程，通过思维的发散，找到三种解决问题的办法，教师通过“追问”，将发散的思维再次聚焦，体会问题的本质。

（三）对比中“追问”，把握本质

策略属于方法的范畴，但又不同于一般的方法，而是一种“高级方法”。“解决问题的策略”教学的实质是借助策略帮助学生寻求合适的解决问题的途径。对比是让学生把握知识本质的一种常用的方法，通过对比和思辨，能知其然并且知其所以然。在“对比处”追问，引导学生透过现象，进一步能把握策略的本质。

片段3：“对比处”追问

1.对比体会：是不是所有的数学问题都需要利用画图的策略来解决呢？老师带来了两道题。

2.讨论总结：第一道题，数量关系比较清晰，可以直接算出短花边的长度，再计算一共多少厘米，可以不画图。第二题，长花边和短花边的长度都不知道，画线段图整理条件能让问题变得更清晰。

学生尝试后交流方法，有的学生将总数105厘米加上15厘米，将短花边变成长花边；有的学生将总数105厘米减去15厘米，将长花边变成短花边。相较于之前的三种方法，这次没有学生用“移”的方法，这时候，教师追问：

[追问3]这里为什么没有人用“移”这种方法了呢？

在“对比处”适时追问，学生可以选择出更优化的方法。将15厘米分一半给短花边对于四年级的学生来说，牵涉到分数的除法，不好计算。对比中学生逐渐体会到有些方法并不是所有题目中都适用的，在解决问题时，要根据实际情况选择合适的方法，也体现了数学中的“优化”思想。

理解一类问题的本质，是一个循序渐进的过程，需要师生之间不断在问题的引领下探究，逐渐揭开本质的面纱。学生经历了探究两道实际问题解决的过程，是时候了解问题的本质了，这时候教师乘胜追击，继续追问：

[追问4]刚才利用画图的策略解决了两道问题，我们实际上在研究的是什么样的问题？

学生谈论后总结，例题中小春的邮票比小宁多12枚，这道题中短花边比长花边少15厘米，两个量之间都存在着多和少的关系，并且知道它们的和。本节课讨论的主要问题就是“和差”问题，本质就在于想办法将两个量变得同样多，在“对比处”再次追问，促进学生的思维走向深入，把握住一类问题的本质。

（四）拓展中“追问”，体会价值

小学生年龄特点和理解能力决定了在数学学习中，思考问题较为片面化、表层化，缺乏深度和广度。在教学设计时，设计一些拓展性的问题，可以帮助学生从由浅入深，提高思维的广阔性，同时体会问题和策略的价值。

片段4：“拓展中”追问

尝试解决：李娟非常喜欢做花边，她又做了几条花边。尝试解决并想想每一步算的是什么。

这时候花边由2条变成了4条，但是解决问题的方法仍然是设法将花边变得同样长，为了让学生理解策略的价值，教师追问：

[追问5]我们解决了两条花边的问题，又解决了四条花边的问题，如果花边的条数变得更多，你还有信心能解决吗？

策略教学的目的，不仅仅是掌握方法，更是让学生体会策略的价值。教师在“拓展处”追问，从两条花边延伸到四条花边，再拓展到更多条花边，让学生更加深刻的感受此类问题的价值：不管多少个量，我们最终的目的都是借助线段图，将这些不相等的量变成相等的量来解决。

二、课下慎思，提高“追问”教育价值

在课堂的各个环节中，通过“追问”，将教学内容结构化，将问题本质清晰化，同时提高了学生思维的宽度和深度。那么教师在设计“追问”时机和问题时，需要关注什么呢？笔者做了以下反思。

（一）从“散”到“串”，追问让内容结构化

一节数学课中，教师往往重点研究一道问题，解决几个练习，这些知识点和问题之间都存在一定的联系，需要将一些“问题”的探究串在一起，让内容结构化。

在教学“解决问题的策略（画图）”一课时，教师通过五次追问将所有需要解决的问题串成了一个问题链。从简单的一年级“如何将两个量变得同样多”问题解决开始，依次解决“两个量之间的和差问题”“多个量之间的和差问题”。学生在解决这一系列问题的过程中，逐步学会画线段图和看图分析数量关系的方法，同时通过对比和知识的迁移，把握这类问题的实质，从而获得对画图策略的整体认识。

（二）从“浅”到“深”，追问让本质清晰化

在数学课堂中，当学生解决完简单的问题时，很多教师往往会直接进入下一教学环节，错过了再次深入探讨“本质”的好时机，若能在这时通过“追问”往深处探究，必然能将问题本质清晰化。

在教学“解决问题策略（画图）”一课时，在学生初步学会运用策略解决问题之后，教师追问了三次，一次是教师通过“追问”，对比三种方法，帮助学生感受方法的共性；第二次是在以题组形式出现的练习题中，让学生在对比中辨别，从而把握策略的本质，第三次是方法上的对比优化，运用一种策略来解决问题，也会有方法上的不同，学生不仅要会借助策略来解决问题，同样也需要通过对比，灵活选择更为便捷的方法来解决问题。不断的追问，迫使学生往深处思考，拓宽了学生的思维。

（三）从“窄”到“宽”，追问让思维广阔化

“就题讲题”是一种错误的教学方式，它不利于学生的思维发展。教师在教学设计时，要适当思考：通过这道问题，学生能学到什么？思维能得到发展吗？怎样设计能让学生的思维更加广阔化？

在设计“解决问题策略（画图）”时，笔者将书上“练一练”的情境改成了李娟做花边的问题，和练习中“李娟做了四条花边”的问题成为了系列问题，目的是在同一个情境中拓宽学生的思维。学生研究完这两个问题后，通过“追问”再拓展到多条花边的关系，激发学生继续探究的欲望。

“追问”作为课堂中必不可少的环节，如何精准“追问”是值得我们教师深入研究的话题。教学中，我们从学生思维特点出发，在各个教学环节中精准设计“追问”，帮助学生掌握知识、把握本质、提升思维。